Лекции_Микроэкономика

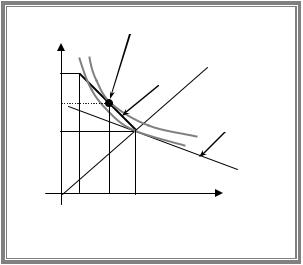
u

u c2

pu c1 1 p u c2 u pc1 1 p c2

Application 1. Obtaining additional information

Mary has a utility function u=50-120/c, where c is her consumption, measured in thousands of dollars. If Mary becomes an economist, she will make 30 thousand per year for certain. If she becomes a pediatrician, she will make $60 thousand if there is a baby boom and $12 thousand otherwise. The probability of a baby boom is p=0.5.

Now suppose a consulting firm has prepared demographic projections that indicate which event will occur. Will she purchase the projection at price of $6000?

As the maximum utility achieved without demographic projection was only 44 Mary would be willing to purchase this projection.

41

losses of L , 0 L w . Individual is offered to purchase insurance with insurance premiumper unit of insurance.

Insurance is actuarially fair if EV $1 p $ 0 or p .

If p , then insurance is unfair. The case of unfair favourable insurance ( p ) is quite unrealistic as insurance company incurs loss under this price.

Thus we will consider only fair and unfavourable insurance.

Two states of the world: “loss” and “no loss”.

Two contingent commodities: cL - consumption in case of loss, cNL - consumption in case of no loss.

Denote by z the quantity of insurance and assume that over-insurance is not allowed (you cannot insure more than L), then

cL w L z zcNL w z

0 z L

If we solve this system with respect to z , then we get the budget constraint of the form:

w-L cL

In case of fair insurance budget constraint coincide with fair odds line and as a result utility is maximised at certainty point, where indifference curve is tangent to budget line, which means

that person will purchase full insurance: cL w L z 1 cNL w z or z L .

42

Thus any risk averse agent under fair insurance purchases full insurance (insures all the loss).

In case of unfair unfavourable insurance ( p ) budget line is steeper than fair odds line. As a result risk averse person will never purchase full insurance. He will either purchase partial insurance ( 0 z L ) or no insurance at all.

Unfavourable insurance

Application 3. Diversification

Consider a risk averse investor with initial wealth, w than he can allocate between two assets. One asset is risk-free with net return equal zero. The other asset is risky. In bad state of the world net return is 1 b 0 and in good state net return is a 0 . The probability of good state is p . Suppose that on average risky project gives higher return bp a 1 p 0 .

Two states of the world: “bad” and “good”.

Two contingent commodities: c1 - consumption in case of bad state, c2 - consumption in case of good state.

Denote by z investment in risky asset (assume 0 z w ), then

43

Conclusion: if risk is favourable, then risk averse agent will invest positive sum in risky asset (i.e. he will diversify).

44

4. THE FIRM

4.1 Modeling the firm’s technological opportunities

Production function is the relationship between the quantities of various inputs used per period of time and the maximum quantity of output that can be produced per period of time:

Q f z1 ,z2 , ,zn .

We are going to concentrate on the case with two inputs: capital (K) and labour (L). Examples of production functions ( 0, 0 ):

Fixed proportions or Leontieff technology min L, K ,

Linear technology L K ,

Cobb-Douglas production function AL K

In case of two inputs we can represent production function graphically in terms of isoquants.

Isoquant is the locus of all the (technically efficient) combinations of inputs for producing a given level of output.

Question: illustrate isoquants for the Leontieff, linear and Cobb-Douglas production functions.

Properties of the production functions.

Marginal physical product of input i - the extra amount of output that can be produced when the firm uses additional unit of this input, holding the levels of other inputs constant:

MPi f .zi

A technology exhibits decreasing/increasing/constant returns to factor when the marginal physical product of an input falls/rises/stays constant as the amount of the input used increases.

Question: characterize the three considered technologies (Leontieff, linear and CobbDouglas) with respect to returns to each factor of production

Marginal rate of technical substitution of labour for capital MRTSLK measures the rate at which the firm has to substitute one input (L) for another (K) in order to keep output (Q)

Definition suggests that MRTS can be calculated as a ratio of the marginal products:

Solution: demand functions for factors of production L p,w,r , K p,w,r and supply of output Q p,w,r

This problem can be divided into 2 sub-problems:

2) profit maximization with respect to output max pQ TC w,r,Q .

Q 0

4.3 Cost minimization

Cost minimization in the long run

In the long-run all factors are variable

TC LR w,r,Q min wL rK

K 0,L 0

F K ,L Q

Graphical solution of cost-minimisation problem

K

Isocost line - a line representing all input combinations that have the same cost for the firm. Equation of isocost: wL rK const

At interior solution the slope of isoquant is equal to the slope of isocost:

MRTSLK L ,K w / r . This condition implies that if the firm uses both factors in equilibrium, then they bring the same marginal product per dollar spent:

Thus if the firm uses both factors, then the corresponding quantities demanded can be found from the following system

47

demand functions are called conditional or derived demand for factors of production since the quantities depend on the level of output produced.

We can look for the optimum input combinations in production for different levels of output, the resulting curve is known as expansion path. Expansion path allows for given factor prices to get a relationship between output and the long run cost.

K

Expansion

path

Q4

Q3

Q1 Q2

Exercise. Illustrate expansion path for the homothetic production function.

Analytically we get he long run cost function by plugging conditional demand functions into the objective function: TC LR w,r,Q wL w,r,Q rK w,r,Q .

Properties of long run costs

Long run marginal cost ( MC LR ) - the change in long-run total cost due to the production of

additional unit of output: MC LR TC LR .Q

Long run average cost ( AC LR ) - the long-run total cost divided by the number of unites

produced: AC LR TC LR .

Q

When long run average costs fall as output rises, costs are said to exhibit economies of scale.

When long run average costs rise with the output level, costs are said to exhibit diseconomies of scale.

Due to homotheticity, K/L ratio under CRS is not affected by the level of output. As a result, with CRS technology to increase output in times we increase the employment of each factor in times. Then cost of production also increases in times, while average cost stay constant:

That is in case of CRS we have neither economies, nor diseconomies of scale.

NOTE: As AC=const, then TC LR cQ , where c - cost of producing of one unit of output. It

implies that AC LR MC LR c .

48

With IRS we can produce Q by increasing the factors’ employment in a smaller proportion,

which implies that total cost also increase by less than times1. As a result AC falls and we deal with economies of scale:

In case of DRS under homothetic production function in order to increase output in times, we increase the factors’ employment in a greater proportion, which implies that total cost also increases in more than times. As a result AC goes up:

That is in case of DRS we have diseconomies of scale.

1 Note if production function isn’t homothetic then proportional factor increase does not necessarily correspond to cost minimizing bundle but this implies that cost minimizing bundle might cost even less.

49