Бусыгин

611

типа равен u0 = 1.

Найдите оптимальный контракт вида {(Q1, w1), (Q2, w2)} в условиях асимметричной информации (заказчик не различает подрядчиков).

34. В модели найма со скрытой информацией с n типами работников (θ= 1, ..., n) покажите, что если µθ = n1, и cθ(x) = θc(x), где c(x) — возрастающая выпуклая функция, то ограни-

чение монотонности усилий несущественно, т.е. задача определения оптимального контракта распадается на n независимых задач.

35. Пусть в модели найма со скрытой информацией cθ(x) = θx, функция дохода y(x) такова, что предельный доход положителен и убывает. Предположим, что решение задачи поиска оптимальных пакетов (x-θ, w-θ) является внутренним, причем все типы работников подписывают контракт.

(A) Покажите, что если имеется два типа работников, θ1 и θ2, причем θ1 < θ2, то уровни усилий удовлетворяют соотношениям

y′(x-2) = θ−2 + µµ1 (θ−1 – θ−2),

2

а

y′(x-2) = θ−1.

(B) Покажите, что если имеется три типа работников, θ1, θ2 и θ3, причем θ2 – θ1 = θ3 – θ2 > 0, то ограничение монотонности усилий является существенным тогда и только тогда, когда µ2 < µ1µ3. Вычислите оптимальные пакеты для случая, когда µ2 < µ1µ3 и µ2 >µ1µ3.

(С) Покажите, что если имеются n типов работников, причем

θi – θi–1 = θi+1 – θi > 0,

то достаточным условием несущественности ограничения монотонности усилий является неубывание отношения

µ1 + ... + µi–1.

µi

Покажите, что это достаточное условие, вообще говоря, не является необходимым.

36. Пусть в модели найма со скрытой информацией допустимые усилия задаются условием x >0, функция дохода y(x) обладает следующими свойствами:

(1)y′(x) →∞ при x →0;

(2)y′(x)x →0 при x →0,

и существуют работники двух типов, издержки усилий которых линейны (cθ(x) = θx). Докажите, что наниматель наймет работников обоих типов, т.е. x-θ > 0 θ.

37. Рассмотрим ситуацию ценовой дискриминации следующего типа Единственный производитель и продавец частного блага, производство которого характеризуется постоян-

611

612

ными издержками. сталкивается с двумя типами покупателей этого блага, оценками которых имеют вид

vθ(x) = θ x , θ= 1, 2.

Покупатели двух типов встречаются с вероятностями µ и 1 – µ соответственно. Проинтерпретируйте эту модель как модель найма и найдите оптимальный контракт. Проделайте то же самое для трех типов покупателей.

38. В модели найма со скрытой информацией с двумя типами работников предположим, что издержки усилий работника 1-го типа равны c1(x) = 0,5 x2, работника 2-го типа — c1(x) = x2. Пусть контракт ищется среди линейных по усилиям схем (базовая заработная плата плюс премия за усилия, пропорциональная величине усилий).

Определите характеристики оптимального контракта в зависимости от доли работников первого типа. Сравните с оптимальным пакетным контрактом.

39. На рынке страховых услуг имеются два типа страхователей — с низкой или высокой вероятностью µθ наступления страхового случая — потери актива ценностью K рублей. Во всех других аспектах они одинаковы — каждый обладает каждый богатством W (включая рассматриваемый актив) и его предпочтения характеризуются функцией ожидаемой полезности с элементарной функцией v(w) = ln(w).

На рынке страховых услуг имеется только одна страховая компания

(А) Сформулируйте задачу страховой компании и проинтерпретируйте ее как модели найма со скрытыми типами.

(Б) Каким окажется выбранный страховой контракт, в случае симметричной информации, т.е. в условиях, когда страховая знает тип страхователя?

(В) Каким окажется выбранный страховой контракт, в случае асимметричной информации, т.е. в условиях, когда страховая знает только распределение вероятностей типов страхователя?

(Г) Предположим, что на рынке существует несколько страховых компаний. Какие страховые контракты предложат в этом случае страховые фирмы?

Модель найма со скрытой информацией: конкуренция среди нанимателей

В этом параграфе мы откажется от сделанного ранее предположения о монопольном положении нанимателя и будем считать, что существует по крайней мере два нанимателя, предлагающие контракты работникам, тип которых они не наблюдают.

Будем считать, что другие характеристики ситуации найма остаются без изменения. В частности, как и раньше, будем предполагать, что результат усилий работника не зависит от его типа. Это предположение позволяет рассматривать контракты, обуславливаемые только уровнем усилий (но не результата).

В этой случае игра имеет вид:

0.«Природа» выбирает тип работника.

1.Наниматель j, не зная типа, предлагает ему контракт wj( ), причем все наниматели выбирают контракт одновременно.

612

613

2.Работник (зная свой тип) решает, подписывать ли ему контракт или нет, и если подписывать, то какой из двух.

3.Если работник подписывает j-й контракт, то он (зная свой тип) выбирает уровень усилий x.

Рисунок 147. Представление модели найма со скрытой информацией при конкуренции нанимателей в виде дерева

Охарактеризуем возможные равновесия данной игры — равновесные контракты модели найма при конкуренции нанимателей, — ограничившись характеристикой равновесных пакетов.

Полную игру для целей анализа заменим следующей упрощенной игрой:

0.«Природа» выбирает тип работника.

1.Наниматели одновременно предлагают работнику пакеты (wjθ, xjθ).

2.Работник решает, подписывать ли ему контракт или нет, и если подписывать, то какой из пакетов выбрать.

Мы опускаем формальное доказательство того, что описанные игры в определенном смысле эквивалентны. Такое доказательство можно построить, пользуясь идеями предыдущего параграфа.

Будем предполагать в дальнейшем, что равновесие в игре таково, что в нем работник обязательно подписывает один из предложенных контрактов (ограничение участия выполнено).

Анализируя такую игру с использованием обратной индукции, получим, что равновесные пакеты (x-jθ, w-jθ) характеризуются следующими свойствами:

♦ Работник выбирает (из всех пакетов всех нанимателей) пакет (wjθ, x-jθ), дающий ему максимальную полезность:

w-jθ – cθ(x-jθ) >w-iϕ – cθ(x-iϕ), θ, ϕ Θ, i = 1, 2.

При использовании обратной индукции в этом месте возникает неоднозначность в случае, когда работнику безразлично, пакет какого нанимателя выбрать. Сделаем предположение (аналогичное предположению модели Бертрана), что в этом случае работник использует смешанную стратегию, выбирая нанимателей с одинаковой вероятностью.

♦ Наниматель j предлагает набор пакетов (w-jθ, x-jθ), дающий ему максимальную ожидаемую прибыль при данном наборе пакетов конкурента.

613

614

Для того чтобы упростить анализ, будем предполагать, что функции издержек строго выпуклы.

Прежде, чем рассмотреть модель с ненаблюдаемыми типами, проанализируем ситуацию, когда тип работника известен работодателю. Покажем, что в этом случае решение игры (равновесные пакеты (w-jθ, x-jθ)) имеет вид:

x-jθ = x-θ = x^θ, w-jθ = w-θ = x-θ,

где

x^θ = argmax{x – cθ(x)},

Доказательство этого факта проведем в 2 этапа. Во-первых, покажем, что прибыль каждого нанимателя от найма работника любого типа равна нулю. Пусть это не так, и существует наниматель (например, j = 1) и тип работника, такие что от сделки с этим работником этот наниматель получает положительную прибыль (Π1 > 0). Здесь может быть два случая:

(1) 2-й наниматель предлагает невыгодный работнику контракт и, следовательно, получает нулевую прибыль и (2) работник безразличен между предлагаемыми двумя контрактами. Во втором случае оба нанимателя получают одинаковую положительную прибыль

(Π1 = Π2 > 0).

Тогда 2-й наниматель мог бы предложить этому работнику пакет с тем же уровнем усилий, но несколько более высокой оплатой. Работник тогда выбрал бы пакет, предлагаемый 2-м нанимателем, который получил бы при этом прирост прибыли. В случае (1) в первом приближении прибыль станет равной Π1, а в случае (2) — 2Π1 = 2Π2.

Таким образом, в исследуемом равновесии прибыль каждого нанимателя от найма работника любого типа равна нулю, и, следовательно, оплата усилий равна производимому работником доходу:

w-jθ = x-jθ.

Во-вторых, покажем, что наниматели предлагают работнику типа θ пакет, обуславливающий уровень усилий

x-jθ = x-θ = x^θ.

Действительно, если это не так и, например, первый наниматель предлагает пакет (w-jθ, x-jθ) такой, что

∆= (x^θ – cθ(x^θ)) – x-jθ – cθ(x-jθ) > 0.

Но тогда пакет (x^θ – ∆/2, x^θ) предпочитается работником типа θ и дает предложившему ему нанимателю более высокую прибыль, чем (w-jθ, x-jθ). Но такая ситуация не может возникнуть при равновесии.

Поскольку каждая из рассматриваемых задач имеет единственное решение при строгой выпуклости издержек, то в равновесии все фирмы предлагают работнику каждого из типов θ одинаковые контракты: x-jθ = x^θ j.

614

615

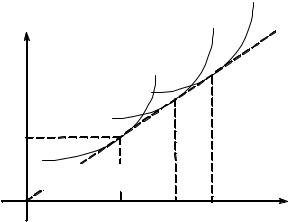
c3(x)+x-3–c3(x-3)

c2(x)+x-2–c2(x-2)

w-3=x^1 w-2=x^2

w-1=x^3

c1(x)+x-1–c1(x-1)

x

-x1=x^1 -x2=x^2 -x3=x^3

Рисунок 148. Равновесные пакеты при наблюдаемости типов, 3 типа работников

Сравнивая это решение с монопольным случаем, отметим, что равновесные пакеты в данном случае характеризуются тем же объемом усилий, но более высокими уровнями оплаты. Мы предполагаем здесь, что рассматривается случай, когда оптимальный «монопольный» пакет дает нанимателю положительную прибыль.

Равновесие оказывается оптимальным по Парето, поскольку благосостояние

W = Ûµθ(xθ – cθ(xθ))

θ Θ

в нем достигает максимума.

Покажем, что эти же пакеты (x^θ, x^θ) составляют единственное равновесие при ненаблюдаемости типов. Докажем, что это равновесие. Во-первых, для этих контрактов выполнены условия совместимости стимулов, т.е.

w-θ – cθ(x-θ) >w-ϕ – cθ(x-ϕ), θ, ϕ Θ,

поскольку в данном случае они имеют вид

x^θ – cθ(x^θ) >x^ϕ – cθ(x^ϕ), θ, ϕ Θ.

Справедливость неравенства следует из определения x^θ.

Во-вторых, ни одна из фирм не может предложить систему пакетов, которая дала бы ей положительную ожидаемую прибыль. Пусть это не так. Тогда эта альтернативная система пакетов содержит пакет, для которого прибыль положительна, и работник одного из типов, например θ, получает от этого пакета более высокую полезность, чем от пакета (x^θ, x^ θ). Этого быть не может, поскольку сумма прибыли фирмы и полезности работника этого типа от любого пакета (w, x) составляет величину x – cθ(x), не превышающую x^θ – cθ(x^θ) по определению x^θ.

Осталось показать, что других равновесий нет.

Ограничимся анализом ситуации с двумя типами работников и двумя нанимателями.

Как и в ситуации с единственным нанимателем, мыслимы два типа равновесий: разделяющие равновесия и объединяющие равновесия. Таким образом, мы должны показать, что в данной ситуации объединяющих равновесий не существует, а любое разделяющее равновесие совпадает с описанным равновесием (равновесием при наблюдаемости типов).

Установим сначала ряд свойств равновесий в ситуации с ненаблюдаемыми типами.

615

616

♣ Если пакеты (w-jθ, x-jθ) являются равновесными, то ожидаемая прибыль каждого нанимателя равна нулю.

Во-первых, в равновесии ожидаемая прибыль каждого нанимателя неотрицательна, поскольку он всегда может предложить непривлекательные пакеты и получить по крайней мере нулевую прибыль.

Во-вторых, все выбираемые любым типом работников θ пакеты равнопривлекательны как для этих работников, так и для предложивших их нанимателей. То, что они равнопривлекательны для работников очевидно. Равнопривлекательность для нанимателей следует из того, что если один из нанимателей получает более низкую прибыль от сделок с работниками типа θ, чем другой, то он мог бы предложить работникам этого типа пакеты своего конкурента. При этом условия самовыявления не нарушаются, поскольку для работников других типов предпочтительны другие пакеты.

Пусть один из нанимателей, например первый, получает положительную прибыль Π1, причем Π1 >Π2. Обозначим через (w-θ, x-θ) — пакет (один из пакетов, если их несколько), который выбирают работники типа θ. Тогда 2-й наниматель может предложить пакеты (w- θ +ε, x-θ), где ε> 0. Каждый из них более привлекателен для работника соответствующего типа θ, чем (w-θ, x-θ), причем ограничения самовыявления не нарушаются. Этот набор пакетов при достаточно малом ε дает нанимателю 2 типа более высокую прибыль (близкую к Π1 + Π2). Следовательно, такие пакеты не могут быть равновесными.

♣ В равновесии прибыль каждого нанимателя от сделки с каждым работником равна нулю, т.е. для любого пакета, который выбирается работниками выполнено w-jθ= x-jθ. Предположим, что это не выполнено для одного из нанимателей. Тогда существует хотя бы один пакет, дающий этому нанимателю положительную прибыль. В этом случае этот наниматель мог бы заменить все пакеты на этот и получить положительную прибыль.

Используя полученные свойства равновесия докажем сформулированное выше утверждение о единственности равновесия. Пусть это не так и существует равновесие, такое что

x-jθ ≠x^θ.

где, как и в случае наблюдаемости типов,

x^θ = argmax{x – cθ(x)}.

Обозначим

∆= x^θ – cθ(x^θ) – (x-jθ – cθ(x-jθ)).

Тогда ∆> 0 и пакет (x^θ – ∆/2,x^θ) более предпочтителен для работника типа θ, и дает нанимателю j положительную прибыль. При этом прибыль от сделок с любыми другими работниками не может уменьшиться, поскольку в равновесии прибыль от любого пакета равна нулю.

Таким образом, равновесные пакеты имеют вид (x^θ, x^θ), ненаблюдаемость типов в этом простом случае не влияет на структуру равновесия. Это равновесие будет Паретооптимальным.

Отметим близкую аналогию данной модели и свойств равновесия с моделью олигополистической конкуренции Бертрана.

Заметим также, что фактически наниматели в данном случае используют линейный контракт вида w(x) = x, т.е. работник получает полностью доход, который он производит.

616

617

Задачи

40.Пусть в модели найма со скрытой информацией имеется два нанимателя и n типов работников с функциями издержек cθ(x) = θx2. Вычислите равновесные пакеты.

41.Пусть в модели найма со скрытой информацией имеется более двух нанимателей. Охарактеризуйте все равновесия.

42.Пусть в модели найма со скрытой информацией имеется два нанимателя и два типа работников с функциями издержек cθ(x) = θx2 и производительностями y(x) = x/θ.

(1)Покажите, что в равновесии любого типа прибыль от сделки любого нанимателя с работником любого типа равна нулю.

(2)Покажите, что не существует объединяющих равновесий.

(3)Покажите, что если существует разделяющее равновесие, то пакет для работников θ= 2 совпадает с его пакетом при наблюдаемости типов, а для θ= 1 определяется условием самовыявления и равенством нулю прибыли от сделки с ними.

(4)При каких условиях на доли работников разных типов равновесие существует. Вычислите равновесные пакеты, когда эти условия выполнены.

(5)При каких условиях равновесие будет Парето-оптимальным?

617

618

Приложение: Элементы теории некооперативных игр

Введение

Теория игр анализирует принятие решений экономическими субъектами (называемыми, в соответствии с установившейся традицией, игроками) в ситуациях, когда на результат этих решений оказывают влияние действия, предпринимаемые другими экономическими субъектами. Такие ситуации принято называть играми.

В настоящее время теория игр проникла практически во все области экономической теории — в экономику общественного сектора, экономику труда, в теорию отраслевых рынков, международную экономику, макроэкономику и т.д. Как оказалось, исследователи, занимавшиеся моделированием экономических и социальных явлений, предлагали решения, которые совпадают с теми или иными концепциями равновесия современной теории игр, еще до того, как эти концепции были сформулированы в явном виде и вошли в инструментарий теории игр. Приведем лишь несколько примеров: модели олигополии (А. Курно, Ж. Бертран, Г. Штакельберг), модель рынка «лимонов» (Дж. Акерлов), модель сигнализирования на рынке труда (М. Спенс), анализ аукционов в условиях неполной информации (У. Викри). Это совпадение не является чем-то случайным. Фактически предлагаемые решения оказывались естественным обобщением лежащих в основе современной неоклассической теории понятия рационального поведения.

Неоклассическая экономическая теория опирается на логику, которой руководствуются люди, осуществляя выбор в самых разных ситуациях повседневной жизни. Покупая те или иные товары, поступая учиться в университет, голосуя за ту или иную партию, решая вступить в брак и даже совершая преступления люди выбирают из двух или более альтернатив исходя из своих предпочтений. Другими словами, в основе неоклассической экономической теории лежит убеждение,227 что любой феномен общественной жизни следует рассматривать как итог взаимодействия рациональных индивидуумов, выбирающих наилучшие (с их точки зрения) альтернативы из тех, которые для них доступны в данной ситуации.

Как правило, последствия решений, принимаемых одним экономическим субъектом, зависят от того, какие решения приняли, принимают или будут принимать другие. В ситуациях, когда эти решения (влияющие на положение экономического субъекта) ему неизвестны,228 естественно считать, что он делает предположения (формирует ожидания) относительно того, какими эти решения могут быть. Тогда естественное обобщение рационального поведения — это оптимальные выборы экономических субъектов при данных ожиданиях.

Однако предположений о рациональности в общем случае оказывается недостаточным для того, чтобы предсказать, какие действия будут выбраны. Необходимо, таким образом, сделать какие-то предположения относительно ожиданий. Следуя сложившейся в экономической теории практике, мы будем здесь анализировать равновесные ситуации — ситуации, при которых ожидания экономических субъектов оказываются оправдавшимися, т.е. ожидаемые ими действия других экономических субъектов совпадают с фактически выбранными. Такой подход позволяет существенным образом сузить область возможных решений.

227так называемый методологический индивидуализм

228например, решения остальных олигополистов в моделях Курно и Бертрана

618

619

Мы не стремились представить здесь сколько-нибудь развернутое изложение теории игр, какой она сложилась к настоящему моменту.229 Цель раздела скорее в том, чтобы дать понятие об идеях и продемонстрировать возможности теории игр в моделировании ситуаций, включающих стратегическое взаимодействие экономических субъектов.

Статические игры с полной информацией

Под статической игрой понимают такую игру, в которой все ее участники принимают решения не зная, какие именно решения принимают другие. Обычно в этом случае говорят, что участники принимают решения одновременно, хотя сама по себе одновременность принятия решений в данном случае не важна. Под играми с полной информацией понима-

ются такие игры, в которых каждый из игроков точно знает характеристики других игроков.230

Нормальная форма игры

Альтернативные действия, которые может предпринять игрок, в контексте статических игр с полной информацией, совпадают с тем, что в теории игр называется стратегиями, по причинам, которые станут ясны из дальнейшего.

Приведем пример статической игры с полной информацией.

Игра 1.231 «Выбор компьютера»

Двое знакомых одновременно выбирают, компьютеры какого типа им купить. Первый предпочитает IBM PC, второй — Макинтош. Обладание компьютером любимого типа первый оценивает в a (a > 0) некоторых условных единиц, а второй — в b (b > 0) условных единиц. Полезность компьютера другого типа для обоих равна нулю. Каждый получает дополнительную выгоду (c > 0), если они выберут одинаковые компьютеры, поскольку в таком случае используемое ими программное обеспечение будет совместимым.

В этом примере каждый из игроков (мы будем их называть «Игрок 1» и «Игрок 2») имеет две стратегии, которые можно условно назвать «IBM» и «Mac». Описанную игру удобно представить в виде таблицы (матрицы) 2×2. В игре имеется четыре исхода: (IBM, IBM), (IBM, Mac) (Mac, IBM) и (Mac, Mac). Каждому исходу соответствует своя клетка таблицы; в этой клетке помещаются соответствующие выигрыши участников.232 Игры такого

229В частности, мы не касаемся тем, относящимся к кооперативной теории игр.

230Точный смысл терминов статическая игра и игра с полной информацией станет ясен из дальнейшего, когда мы рассмотрим динамические игры и игры с неполной информацией (байесовские игры) соответственно.

231Игра представляет собой вариант известной игры «Battle of sexes» — «Борьба полов».

232Мы будем использовать следующее соглашение при изображении матричных игр двух лиц. Игрок, чье имя стоит слева, выбирает строки таблицы и его выигрыши записываются в левом нижнем углу каждой клетки таблицы. Игрок, чье имя стоит сверху, выбирает столбцы таблицы и его выигрыши записываются в

619

620

рода, то есть игры с двумя участниками, каждый из которых имеет конечное число стратегий, принято называть матричными233 играми двух лиц.

Врассмотренном примере можно выделить три элемента: множество игроков, множество стратегий, которые могут выбрать игроки, выигрыши игроков.

И в общем случае, чтобы задать статическую игру с полной информацией, требуется указать перечисленные элементы. Описание игры в виде такого набора называется нормальной формой игры.234 Можно сказать, предваряя дальнейшее, что это тот минимум, который необходим для описания любой игры. В более сложных типах игр становятся важными и другие аспекты анализируемой ситуации, такие как очередность ходов, информированность игроков, и т.д.

В дальнейшем, описывая общую статическую игру m лиц с полной информацией, будем использовать следующие формальные обозначения для указанных элементов.

Множество игроков (множество участников) будем обозначать I:

I = {1,...,m}.

Множество возможных стратегий i-го игрока — или просто множество стратегий i-го игрока — будем обозначать через Xi. Отдельную стратегию i-го игрока будем, как правило, обозначать через xi. Совокупность стратегий всех игроков будем называть исходом игры. Т.е. исход игры — это набор

x = (x1, ..., xm), где x X1 × ×Xm = X.

Будем предполагать, что у каждого из игроков есть своя целевая функция (в экономической теории ее называют функцией полезности). Обозначим целевую функцию i-го игрока через ui( ). Каждому исходу игры она сопоставляет некоторое действительное число — выигрыш. Таким образом, в описании игры следует задать для каждого игрока i I функцию вида

ui : X & Ê.

Нормальная форма игры, в соответствии со сказанным выше, представляет собой набор

G = I, {Xi}I , {ui}I .

правом верхнем углу. При таком расположении проще понять где чья стратегия и где чей выигрыш. Свой выигрыш всегда расположен ближе к игроку, чем выигрыш партнера.

233точнее биматричными

234Ее также называют стратегической формой игры. Впервые явная формулировка нормальной формы игры была дана в основополагающей статье Джона фон Неймана (Von Neumann, J. (1928), "Zur Theorie der Gesellschaftsspiele," Mathematische Annalen, 100, 295-320. Рус. пер. Дж. фон Нейман, К теории стратегиче-

ских игр, в сборн. "Матричные игры", под ред. Н. Н. Воробьева, М.: Физматгиз, 1961, 173-204. См. также von Neumann, J., and O. Morgenstern (1944), Theory of Games and Economic Behavior. Princeton. Princeton University Press. Рус. пер. Дж. фон Нейман, О. Моргенштерн, "Теория игр и экономическое поведение", М.:

Наука, 1970.)

620