Бусыгин

571

чает, что по наблюдаемым значениям y~ нельзя однозначно определить, какие действия работник выбрал (или не мог выбрать). Такое предположение позволяет избавиться от многих технических сложностей.

Кроме того, естественно предположить, что чем больше усилия, тем более высоким должен быть результат. Поэтому будем предполагать, что распределение Fx( ) «сдвигается вправо» при росте x, т.е.

Fx1(y) > Fx2(y) при x1 < x2.

Это означает221, что Fx2 стохастически доминирует Fx1 при x1 < x2. Из этого свойства следует, что чем больше усилия, тем больше ожидаемый доход:

Ex1y~< Ex2y~ при x1 < x2.

Математическое ожидание берется по распределению Fx, следовательно, оно зависит от того, какие действия x выбрал работник. Соответственно, оператор математического ожидания мы будем писать в виде Ex. Предполагают, что наниматель нейтрален к риску, т.е. его функция выигрыша — ожидаемая прибыль. Т.е. наниматель стремиться максимизировать величину

ExΠ= Ex(y~– w~),

где w~ — оплата по контракту, которая, вообще говоря, является случайной величиной.

Работник максимизирует U = Exu — математическое ожидание элементарной функции полезности u(x, w), которая, как и раньше, зависит от объема усилий x и от вознаграждения w.

Условие участия, по аналогии со случаем полной информации, состоит в том, что работник соглашается на работу по контракту только в том случае, если его ожидаемая полезность при этом не меньше, чем его резервная полезность u0:

Exu >u0.

Для упрощения анализа чаще всего рассматривают частные случаи, когда функция u(x, w) имеет простой вид. Две самых популярных спецификации функции полезности работника имеют следующий вид:

u(x, w) = v(w – c(x))

и

u(x, w) = v(w) – c(x),

где v( ) — возрастающая вогнутая функция, а c( ) — возрастающая выпуклая функция.

Оба типа функции сепарабельны по w и x (первая в каком-то смысле еще и квазилинейна по зарплате w), и включают функцию v( ), позволяющую моделировать отношение работника к риску (риск может быть связан с тем, что получаемая им оплата w является случайной величиной). Нейтральный к риску работник будет иметь линейную возрастающую функцию v( ), которую без потери общности можно считать равной v(z) = z. Поэтому мы будем называть работника нейтральным к риску, если

u(x, w) = w – c(x).

221 Более точно, речь идет о стохастическом доминировании первого порядка.

571

572

Как правило, предполагается, что работник не склонен к риску, то есть функция v( ) вогнута222. Работник является рискофобом, если функция v( ) строго вогнута. При этом, если v( ) дифференцируема, то она имеет положительную убывающую производную.

Поскольку действия x ненаблюдаемы, то оплата по контракту не может быть обусловлена предпринимаемыми работником действиями (усилиями) x. В предположении, что наблюдаемыми являются результаты y~ этих усилий, рассмотрим модель контрактных отношений, при которых оплата по контракту обуславливается полученными результатами (как сигналами относительно уровня усилий). Поэтому в рассматриваемой модели с ненаблюдаемыми действиями контракт — это функция вида w =w(y).

Как и ранее, мы будем предполагать, что наниматель, выбирая контракт, знает функцию полезности и резервную полезность работника, а работник принимает контракт как данный. Таким образом, модель представляет собой динамическую игру. Последовательность ходов в этой игре следующая:

1.Наниматель предлагает контракт w( ).

2.Работник выбирает, работать ему или нет.

3.Работник, если он подписал контракт, выбирает уровень усилий x.

4.«Природа» при данном x по распределению Fx случайным образом «генерирует» y~.

Контракт представляет собой дележ дохода y между нанимателем и работником, и, тем самым, задает их выигрыши.

Наниматель

w( )

Работник

0u0

x

[F ] Природа

x y~

Ex(y~– w(y~))Exu(w(y~), x)

Рисунок 135. Представление модели наниматель-работник с ненаблюдаемыми действиями в виде дерева

Для поиска решения этой модели можно воспользоваться обратной индукцией. При заданном контракте w( ) оптимальный для работника уровень усилий является решением следующей задачи:

U = Exu(w(y~), x) → max x X .

Учитывая это, задача поиска оптимального для нанимателя контракта имеет следующий вид:

Ex*Π= Ex*(y~– w(y~)) → max x*, w( )

Ex*u(w(y~), x*) >Exu(w(y~), x), x X

222 Ясно, что функция v( ) моделирует отношение к риску только с точки зрения, w, но не с точки зрения x. Но для нас это несущественно, поскольку в данной модели усилия x не являются случайными.

572

573 (ограничение совместимости стимулов),

Ex*u(w(y~), x*) >u0

(ограничение участия).

Объяснение того, почему задача нанимателя включает выбор усилий x*, такое же, как для модели с наблюдаемыми действиями: работник предполагается «благожелательным» по отношению к нанимателю, в том смысле, что из равновыгодных для себя действий готов выбрать выгодные для нанимателя223.

Проанализируем сначала случай с наблюдаемыми действиями, но со случайными результатами. Это даст нам «идеальную» точку отсчета для анализа модели с ненаблюдаемыми действиями. При этом, как и выше (в ситуации, когда результат однозначно определяется выбором уровня усилий), рассмотрим вспомогательную задачу, в которой определятся оптимальные для нанимателя значения x и w при ограничении участия:

Ex(y~– w) → max x, w

Exu(w, x) >u0.

Поскольку здесь как w, так и x — детерминированные величины, то u(w, x) — тоже детерминированная. Таким образом, задача сводится к следующей:

При

u(x, w) = v(w) – c(x),

выражая w из ограничения участия, получаем следующую задачу:

Exy~– v–1(c(x) + u0) → max x. ( )

Как и раньше, обозначим соответствующую «идеальную» ситуацию (x^, w^). Если из задачи ( ) найден эффективный уровень усилий x^, то соответствующая плата должна быть равна

w^ = v–1(c(x^) + u0).

Как и при однозначности результата, эту идеальную ситуацию можно реализовать бесконечным числом способов в виде контракта w( ), зависящего от усилий x. (Например, можно использовать пакетный контракт). Кривая w(x) должна лежать под кривой v–1(c(x) + u0) и касаться ее в точке (x^, w^). При этом достигается Парето-оптимум с точки зрения соответствующих целевых функций: ожидаемой прибыли Ex(y~– w~) и ожидаемой полезности

Exv(w~) – c(x).

Действительно, если от произвольной оплаты w~, перейти к фиксированной оплате Exw~, то ожидаемая прибыль не изменится, а ожидаемая полезность не уменьшится (поскольку работник не склонен к риску). Поэтому достаточно рассматривать только случаи, когда плата не случайная. При этом, как несложно понять, записанная выше задача ( ) представляет собой задачу, характеризующую Парето-оптимальные состояния.

Предположим теперь, что действия (усилия) ненаблюдаемы. Поскольку оплату по контракту можно обуславливать только наблюдаемыми величинами, то приходится обуслав-

223 Это предположение базируется на том, что наниматель может простимулировать благожелательные действия работника (доплатить ему).

573

574

ливать величина оплаты в данной ситуации может зависеть только от результата y. Таким образом, из всех рассмотренных выше контрактов (для модели с наблюдаемыми действиями) можно реализовать только линейный по результатам контракт:

w(y) = a + by.

который является оптимальным по Парето в случае, если это контракт с полной ответственностью:

w(y) = y – A.

Покажем, что наилучший для нанимателя контракт вида w(y) является оптимальным по Парето лишь при ограничительных предположениях относительно отношения к риску работника. Об этом свидетельствуют следующие два утверждения.

Теорема 1

Если работник нейтрален к риску, то наилучший для нанимателя контракт с полной ответственностью является Парето-оптимальным и эквивалентен с точки зрения ожидаемой прибыли и ожидаемой полезности эффективному состоянию (x^, w^).

Доказательство.

Ожидаемая прибыль в данной ситуации равна Ex(y~– y~– A) = A, а ожидаемая полезность равна Ex(y~– A) – c(x) = Exy~– A – c(x).

Задача максимизации ожидаемой полезности по x эквивалентна задаче ( ), учитывая, что при нейтральности к риску v–1(w) = w. Таким образом, работник выберет эффективные усилия. Параметр наилучшего для нанимателя контракта с полной ответственностью находится из условия участия:

A = Exy~– c(x) – u0.

При этом ожидаемая полезность равна u0, а ожидаемая прибыль равна Exy~– c(x) – u0 (где x

— эффективные усилия), то есть она такая же, какая достигается в задаче ( ).

*

Очевидно, что описанный в теореме контракт224 является не только оптимальным по Парето, но и оптимальным для нанимателя среди всех возможных контрактов, и факт ненаблюдаемости усилий в данном случае несущественен, поскольку этот контракт решает задачу максимизации ожидаемой прибыли при единственном ограничении — ограничении участия. (Это Парето-оптимальное состояние, в котором один из игроков получает минимальный выигрыш. Следовательно, другой игрок получает максимально возможный выигрыш). Фактически при нейтральности работника к риску модель сводится к модели с наблюдаемыми действиями. Но по существу это единственная содержательно интересная ситуация, когда ненаблюдаемость усилий не имеет значения, что и показывает следующее утверждение.

Теорема 2

224 Ясно, что то же самое верно и для любого другого контракта, который приводит к тем же ожидаемым выигрышам.

574

575

Если работник — рискофоб, и допустимый контракт w( ) таков, что w~ = w(y~) — нетривиальная случайная величина, то соответствующая ситуация не является оптимальной по Парето, поскольку можно увеличить ожидаемую прибыль, не уменьшая ожидаемой полезности.

Доказательство.

Действительно, в данной ситуации можно случайную оплату w~ заменить на ее безрисковый эквивалент. При этом по определению ожидаемая полезность работника не изменится, ожидаемая же прибыль вырастет (у рискофоба безрисковый эквивалент нетривиальной случайной оплаты строго меньше математического ожидания такой оплаты).

*

Из этого утверждения следует, что контракт с полной ответственностью в случае работника — рискофоба не будет Парето-оптимальным, поскольку w~ = y~– A — нетриви-

альная случайная величина. Это связано с тем, что наниматель заинтересован в известной степени застраховать такого работника.

Другое следствие состоит в том, что если при ненаблюдаемости действий работник является рискофобом, то Парето-оптимальность достижима только в случае, когда плата w(y~) детерминированная. Ясно, что такой контракт не является стимулирующим и работник, работая по нему, будет делать наименьшие возможные усилия x = min(X) (если соответствующий минимум существует). Следовательно, Парето-оптимальность достижима только если среди эффективных контрактов есть контракты с минимальными возмож-

ными усилиями, то есть только в содержательно неинтересном случае, когда нанимателю нет смысла стимулировать работника, достаточно дать ему минимальную плату, обеспечивающую резервную полезность. В этом случае наниматель заинтересован полностью застраховать работника.

В общем случае, как мы увидим далее, оптимальный контракт — это компромисс между двумя противоположными целями, которые преследует наниматель: целью стимулирования работника выполнять выгодные для нанимателя действия и целью страхования работника от риска.

Заметим, что предположение о том, что носитель распределения y~ не зависит от величины усилий x является существенным для проводимого здесь анализа. Так, в крайнем случае зависимости носителя распределения y~ от усилий — когда эти носители при разных действиях не пересекаются — по результату можно однозначно установить, предпринимал ли работник те или иные усилия. В этом случае усилия оказывается наблюдаемыми косвенным образом, и оптимальный контракт оказывается тем же, что и в случае наблюдаемых усилий.

Дискретный вариант модели со скрытыми действиями

Рассмотрим модель в дискретном случае: конечное число возможных действий (xa, a = 1, ..., k) и конечное число возможных результатов (ys, s = 1, ..., m). Поскольку сам по себе уровень x не имеет значения, то вместо x мы будем использовать a и обозначим c(xa) = ca, предполагая, что усилия xa растут с ростом индекса a. Каждое значение выбранных работником усилий a приводит к случайному результату y~, который описывается следующим дискретным распределением:

575

576

Здесь µas > 0 — вероятность s-го результата в случае, когда работник выбрал усилия a. По определению вероятностей Ûs µas = 1. Мы будем предполагать, что все ys различны и возрастают по s. По предположению, распределение сдвигается вправо при росте усилий (вероятность более высоких результатов возрастает с ростом усилий), т.е.

Исходные данные для дискретной модели (возможные уровни усилий, уровни результатов и вероятности) можно представить в виде следующей таблицы:

Ниже мы будем предполагать, что элементарная функция полезности имеет вид225:

u(a, w) = v(w) – ca.

Контракт задается величинами ws = w(ys) — каждому возможному результату ys контракт сопоставляет уровень оплаты ws. Таким образом, контракт представляет собой вектор w= {ws}. С другой стороны, это дискретная случайная величина w~.

При этом ожидаемая полезность (как функция от a) равна

U(a, w) = Ea[v(w) – ca] = Ûs µasv(ws) – ca,

а ожидаемая прибыль —

Πe(a, w) = EaΠ= Ea(y~– w~) = Ûs µas(ys – ws).

Задача нанимателя имеет вид:

Πe(a*, w) → max a*, w

U(a*, w) >U(a, w), a =1, ..., k,

(ограничение совместимости стимулов),

U(a*, w) >u0

(ограничение участия).

Поскольку число возможных усилий конечно, то эту задачу вообще говоря, можно решать перебором. Для этого, задавшись конкретным a*, следует найти контракт w= w(a*), минимизирующий ожидаемый уровень оплаты при условии, что при данной оплате работник предпочтет (выберет) уровень усилий a*. Обозначим ожидаемый уровень оплаты

we(a, w) = Eaw~ = Ûs µasws.

Тогда соответствующая вспомогательная задача имеет следующий вид:

we(a*, w) → min w

U(a*, w) >U(a, w), a =1, ..., k,

U(a*, w) >u0.

225 Некоторые альтернативные модели найма представлены в задачах

576

577

В этой задаче искомыми переменными являются только уровни оплаты для различных результатов, т.е. величины ws. Соответствующее максимальное значение ожидаемой прибыли равно Πe(a*, w(a*)). Вычислив для каждого возможного уровня усилий a*=1, ..., k соответствующие значения прибыли, можно найти такое усилие, при котором ожидаемая прибыль (Πe(a*, w(a*)) достигает максимума. Если вспомогательная задача не имеет допустимых решений, то не существует контрактов, обеспечивающих такой уровень усилий, т.е. усилия оказываются нереализуемыми. Поэтому оптимум ищется только по реализуемым усилиям, множество которых всегда не пусто (усилия с минимальными издержками всегда реализуемы).

Поскольку элементарная функция полезности имеет специальный вид

u(a, w) = v(w) – ca,

то эту задачу можно свести к задаче выпуклого программирования (минимизация выпуклой функции на выпуклом многогранном множестве) путем замены переменных vs = v(ws). Как ограничение участия, так и ограничение совместимости стимулов будут в новых переменных линейными, а ожидаемая прибыль — вогнутой функцией переменных vs:

Πe(a, v) = Ûs µas(ys – f(vs)),

где через f( ) мы обозначили v–1( ). (Так как v( ) вогнута, то f( ) выпукла, а –f( ) вогнута). Область определения переменных vs совпадает с областью значений функции v( ) и ее описание должно в явном виде присутствовать в формулировке соответствующей задачи. В дальнейшем мы будем предполагать, что решения рассматриваемых задач являются внутренними.

ДИСКРЕТНЫЙ ВАРИАНТ МОДЕЛИ НАЙМА С ДВУМЯ ВОЗМОЖНЫМИ УРОВНЯМИ УСИЛИЙ

Предположим, что работнику доступны только два действия (два уровня усилий). Обозначим их через H и L (высокий и низкий уровень усилий соответственно). По предположению о том, что распределение сдвигается вправо при росте усилий, имеем:

Напомним, что при конструировании оптимального контракта предварительно определятся величины Πe(L, w(L)), Πe(H, w(H)). Далее выбирается усилие (и соответствующий ему контракт), при котором величина Πe(a, w(a)), a = L, H является максимальной.

Охарактеризуем оптимальный контракт a (a = L, H), обеспечивающий нанимателю ожидаемую прибыль Πe(a, w(a)) (решение вспомогательной задачи с уровнем усилий a).

Если работник совершает действия a, то ожидаемая прибыль нанимателя равна

Ûs µas(ys – ws).

Будем предполагать, что работник является рискофобом, а наниматель нейтрален к риску. Ожидаемая полезность работника в случае, когда он выбирает действие a, будет равна

Ûs µasv(ws) – cL,

Тогда, в случае, если a = L, условие совместимости стимулов имеет следующий вид:

Ûs µLsv(ws) – cL >Ûs µHsv(ws) – cH,

а условие участия:

Ûs µLsv(ws) – cL >u0,

577

578

Соответствующая вспомогательная задача — минимизировать ожидаемую оплату по контракту (максимизировать ожидаемую прибыль)

Ûs µLs ws →min w

(соответственно, Ûs µLs(ys – ws) →max w) при указанных условиях совместимости стимулов и участия.

Рассмотрим сначала простейший случай, когда возможны всего два результата (исхода):

Второе слагаемое здесь положительно при cL < cH. Таким образом, линия совместимости стимулов в координатах (v1, v2) — это прямая, параллельная биссектрисе и проходящая выше нее. Допустимые точки лежат ниже этой линии.

Ограничение участия

µL1v1 + µL2v2 – cL >u0,

можно записать в виде

v >u0 + cL – µL1v1.

2 µL2

Оно задается прямой, наклон которой равен –µL1/µL2. Допустимые точки лежат выше этой прямой. Это одна из линий безразличия работника. (Все линии безразличия работника имеют одинаковый наклон –µL1/µL2).

Чтобы записать задачу нанимателя в терминах полезности обозначим через f( ) функцию, обратную к v( ), то есть f(vs) = ws:

ELΠ~ = µL1(y1 – f(v1)) + µL2(y2 – f(v2)).

Соответствующие кривые безразличия выпуклы вправо вверх, множество лучших точек лежит под кривой безразличия.

Наклон кривой безразличия нанимателя определяется следующим образом:

∂(ELΠ~)/∂v1 = – µL1f′(v1) = – µL1v′(w2). ∂(ELΠ~)/∂v2 µL2f′(v2) µL2v′(w1)

Кривая безразличия нанимателя касается прямой, определяемой условием участия, в точке, где

578

579

Т.е. v′(w1) = v′(w2), что при убывании v′( ), означает, что точка касания соответствует фиксированной оплате w1 = w2, то есть лежит на биссектрисе.

Поскольку в случае, когда a = L, линия, соответствующая ограничению совместимости стимулов, лежит выше биссектрисы, то ограничение совместимости стимулов неактивно. Следовательно, на диаграмме в координатах (v1, v2) оптимальное решение лежит на биссектрисе v1 = v2.

Таким образом, при a = L оплата по контракту должна быть фиксированной: w1 = w2 = w- (контракт с полным страхованием работника).

v2

решение

v1

линии уровня нанимателя

Рисунок 136

Аналогичным образом можно показать, что w1 = w2 = w- и в случае, когда cL = cH. Обратно, если оплата по контракту не зависит от результатов, из условия совместимости стимулов следует, что

-v – cL >-v – cH,

или

cH >cL,

Из этого можно сделать вывод, что оплата по контракту, принуждающему к действиям L, будет фиксированной в тех и только в тех случаях, когда действия типа L требуют от работника меньших затрат, чем действия типа H, то есть являются для него выгодными сами по себе.

Таким образом, для низких усилий линия совместимости стимулов лежит выше биссектрисы, контракт должен изображаться точкой на биссектрисе, и активным является только ограничение участия.

Проанализируем теперь случай, когда наниматель хочет побудить работника выбрать высокий уровень усилий H. Условие совместимости стимулов в этом случае записывается в виде

µH1v1 + µH2v2 – cH >µL1v1 + µL2v2 – cL.

Множество допустимых по этому условию контрактов имеет ту же границу, что и при L (она параллельна биссектрисе и лежит выше ее), но допустимые точки лежат выше границы:

579

580

µH1v1 + µH2v2 – cH >u0,

задается прямой

v = u0 + cH – µH1v1.

2 µH2

Ее наклон равен –µH1/µH2. Поскольку точка касания соответствующих кривых безразличия работника и нанимателя лежит на биссектрисе и поэтому в данном случае не принадлежит множеству допустимых контрактов, ограничение совместимости стимулов оказывается активным.

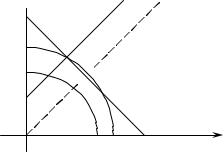
В предположении, что активным является и ограничение участия, решение представляется точкой пересечения двух соответствующих прямых (см. Рис.???). Линии уровня нанимателя в точке пересечения с биссектрисой имеют тот же наклон –µH1/µH2, что и линия участия (это проверяется так же, как для L).

v2

решение

v1

Рисунок 137

Оптимальное для нанимателя решение не является оптимальным по Парето. Оптимальное решение находится в точке A, которая лежит на пересечении линии совместимости стимулов h, и линии участия i. Оно не оптимально по Парето, так как точка B лежит на той же кривой безразличия нанимателя, а для работника она дает большую ожидаемую полезность, чем A (лежит на более высокой линии безразличия работника i′). Точка B является Парето-оптимальной (кривые безразличия касаются), но ее нельзя реализовать как равновесие из-за условия совместимости стимулов. Если же наниматель изменит контракт так, что работнику станет доступна точка B, то работнику будет выгодно изменить свои действия с H на L. Действительно, на диагонали выполняется неравенство

µL1v + µL2v – cL > µH1v + µH2v – cH.

При переходе от H к L карта кривых безразличия работника в координатах (v1, v2) меняется, так как меняются вероятности. Соответствующей точке B линией безразличия будет i′′. В то же время

ELΠ~ = µL1(y1 – f(v)) + µL2(y2 – f(v))EHΠ~ = µL1(y1 – f(v)) + µL2(y2 – f(v)).

Наниматель должен ограничивать полезность работника, чтобы тот не выбрал еще большую в ущерб интересам нанимателя.

580