601
следует, что
wθ – cθ(xθ) >wϕ–1 – cϕ–1(xϕ–1) + cϕ–1(xϕ) – cθ(xϕ).
Поскольку из ограничения задачи ( ) xϕ–1 >xϕ, а функция cθ(x) – cϕ–1(x) возрастает, то
cθ(xϕ–1) – cϕ–1(xϕ–1) >cθ(xϕ) – cϕ–1(xϕ),
откуда
wθ – cθ(xθ) >wϕ–1 – cθ(xϕ–1).
*
Данная теорема (цепное правило) позволяет получить ряд свойств системы оптимальных пакетов. В частности, из ограничений задачи ( )
w-θ – cθ(x-θ) = w-θ+1 – cθ(x-θ+1)
и монотонности усилий
x-θ >x-θ+1.
следует, что w-θ <w-θ+1, то есть плата монотонна (не убывает по типу).
Напомним, что излишек, получаемый работником, называют информационной рентой. Для работника типа θ она равна
w-θ – cθ(x-θ) (>0).
Эта рента не возрастает по θ, поскольку
w-θ – cθ(x-θ) = w-θ+1 – cθ(x-θ+1) >w-θ+1 – cθ+1(x-θ+1).
Если для какого-то из типов информационная рента положительна, то для всех предыдущих типов она тоже положительна. Для работника n-го типа информационная рента равна нулю. Рента нужна, чтобы работник не стал «притворяться», что его тип более высокий, чем на самом деле (в обратную сторону претворяться не имеет смысла).
Можем выразить {w-θ} через {x-θ} следующим образом: w-n = cn(x-n),
w-n–1 = w-n – cn–1(x-n) + cn–1(x-n–1) = cn(x-n) – cn–1(x-n) + cn–1(x-n–1),
и т.д. Получим зависимость w-θ = w-θ(x-θ, ..., x-n). Общая формула имеет следующий вид
n
w-θ(xθ, ..., xn) = Û (ck(xk) – ck–1(xk)) + cθ(xθ).
k=θ+1
Таким образом, задача ( ) сводится к следующей:
Ûµθ(xθ – w-θ(xθ, ..., xn)) → max {xθ}
θ Θ
xθ >xθ+1, θ< n.
Объединяя слагаемые, являющиеся функциями от xθ, получим эквивалентную запись этой задачи:
Û[µθ(xθ – cθ(xθ)) – Μθ–1(cθ(xθ) – cθ–1(xθ))] → max {xθ}
θ Θ

602
xθ >xθ+1, θ< n.
где мы ввели обозначение
Μθ = µ1 + ... + µθ.
Поскольку целевая функция задачи сепарабельна по {xθ}, то в ситуации, когда ограничения монотонности усилий по типу xθ >xθ+1 несущественны, ее решение распадается на n независимых друг от друга задач:
x – cθ(x) – Μµθ–1(cθ(x) – cθ–1(x)) → max x X.
θ
Как мы видели, для случая 2 типов решения соответствующих задач x-1, x-2 всегда удовлетворяют условию x-1 > x-2, однако в общем случае такого распадения задачи может не быть. Следующий пример показывает, что в случае 3 типов работников ограничение xθ >xθ+1 может стать активным.
Пример 4.
Пусть на рынке труда, в дополнение к 2 типам работников, рассмотренным в Примере 3, с функциями издержек
c1(x) = 0,5 x2, c2(x) = x2,
имеются также работники 3-го типа с функцией издержек
c3(x) = 1,5 x2.
Решение задачи
x – c3(x) – µ1µ+ µ2(c3(x) – c2(x)) → max
3
имеет вид:
1
x-3 = 3 + (µ1 + µ2)/µ3.
Если доля работников 2-го типа, µ2, мала, то решение аналогичной задачи для работника 2-го типа может оказаться ниже:
|
1 |
|
< |
|
|
1 |
|
, |
2 |
+ µ /µ |
3 |
+ (µ + µ )/µ |
|
|
1 |
2 |
|
|
1 |
2 |
3 |
то есть разделяющий контракт не будет оптимальным. Это происходит при µ2 < µ1µ3. На-
пример, при µ1 = 3/8, µ2 = 1/8, µ3 = 1/2 получим x-2 = 1/5 и x-3 = 1/4.
Чтобы получить уровни усилий, которые определяют оптимальный контракт в этом случае, следует решить задачу
µ2(x – c2(x)) – µ1(c2(x) – c1(x)) +
+ µ3(x – c3(x)) – (µ1 + µ2)(c3(x) – c2(x)) → max
или
(µ2 + µ3) x – (2 + µ2 + µ3) x2 → max 2
откуда получаем следующие параметры объединяющего контракта:

603
µ + µ x-2 = x-3 = 2 +2µ2 +3µ3,
|
|
|
|
|
|
µ + µ |
3 |
2 |
w- |
|
= w- |
|
= c (x- ) = 1,5 |
|
2 |
. |
|
|
|
|
|
2 |
|
3 |
3 3 |
2 + µ + µ |
|
|
|
|
|
|
|
2 |
3 |
Как и в Примере 3 x-1 = 1, однако оплата будет другая:
|
|
|
|
|
|
µ + µ |
3 |
2 |
w- |
|
= w- |
|
+ c (x- ) – c (x- ) = 0,5 + |
2 |
. |
|
|
|
|
|
1 |
|
2 |
1 1 1 2 |
2 + µ + µ |
|
|
|
|
|
|
|
2 |
3 |
При µ1 = 3/8, µ2 = 1/8, µ3 = 1/2 получим x-2 = x-3 = 5/21.
Записав для полной задачи, включающей ограничение x2 > x3, функцию Лагранжа и приравняв к нулю ее производные в найденном решении, можно убедится, что множитель Лагранжа для данного ограничения равен
µ3µ1 – µ2 .
2 + µ2 + µ3
Таким образом, ограничение активно при µ2 < µ1µ3.
c3(x) c1(x)
c2(x) 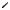 w-1
w-1 










x-1
Рисунок 143. Пакеты, соответствующие объединяющему контракту для 3 типов работников
Оптимальные контракты можно разделить на два класса:
Разделяющие контракты: x-θ > x-θ+1 θ — все типы себя выявляют.
Объединяющие контракты: θ: x-θ = x-θ+1, w-θ = w-θ+1 — существуют кластеры (эффект группирования типов (bunching) ). Работники нескольких разных типов делают одинаковые усилия и получают одинаковую зарплату. Таким образом, рассмотренный пример описывает случай группирования второго и третьего типа, т.е. случай (частично) объединяющего контракта.
При дополнительных предположениях о поведении функций издержек в зависимости от типа и усилий работника, а также формы функции распределения типов можно гарантировать, что оптимальный контракт является разделяющим.
Обозначим, как и выше,
dθ(x) = cθ+1(x) – cθ(x).
Мы предположили, что dθ(x) — возрастающие функции. Предположим дополнительно, что dθ+1(x) – dθ(x) — тоже возрастающие функции.

604
В этом случае задача ( ) эквивалентна следующей (получаемой из нее удалением ограничений монотонности усилий xθ >xθ+1):
Ûµθ(xθ – wθ) → max |
{wθ, xθ} |
|
θ Θ |
|
|
wθ – cθ(xθ) = wθ+1 – cθ(xθ+1), θ< n, |
( ) |
wn – cn(xn) = 0.
Таким образом, в этом случае задача составления оптимальных пакетов сводится к решению последовательности n независимых задач.
Теорема 4.
Предположим, что dθ(x) и dθ+1(x) – dθ(x) возрастают по x θ и |
Μθ–1 |
возрастает по θ. То- |
µθ |
гда задачи ( ) и ( ) эквивалентны. |
|
|
Доказательство. |
|
|
Для доказательства утверждения достаточно показать, что решения {x-θ} задач
Πθ(x) = x – cθ(x) – Μµθ–1dθ–1(x) → max x X.
θ
удовлетворяют опущенным ограничениям (монотонности).
Поскольку x-θ максимизирует Πθ(x), а x-θ+1 максимизирует Πθ+1(x), то выполняются неравенства
Πθ(x-θ) >Πθ(x-θ+1)
и
Πθ+1(x-θ+1) >Πθ+1(x-θ).
Сложив эти неравенства, после преобразований получим:
|
Μθ–1 |
|
Μθ |
Μθ–1 |
|
|
µθ |
[dθ(x-θ) – dθ–1(x-θ)] + (1 + |
µθ+1 – |
µθ )dθ(x-θ) > |
> |
Μθ–1 |
|
|
Μθ |
Μθ–1 |
)dθ(x-θ+1). |
µθ |
[dθ(x-θ+1) – dθ–1(x-θ+1)] + (1 + µθ+1 |
– µθ |
Поскольку в предположениях теоремы функция |
|
|
|
|
|
|
Μθ–1 |
|
Μθ |
|
Μθ–1 |
|
|
µθ [dθ(x) – dθ–1(x)] + (1 + |
µθ+1 |
– |
µθ )dθ(x) |
является возрастающей, то x-θ >x-θ+1.
*
Если к сделанным предположением добавить предположение о дифференцируемости функций, то можно доказать, что x-θ > x-θ+1 для внутренних решений. По условиям первого порядка
|
|
|
|
|
|
|
|
|
|
|
605 |
|
|
|
Πθ′(x-θ) = 1 – cθ′(x-θ) – Μθ–1dθ′–1(x-θ) = 0. |
|
|
|
|
|
|
|
µθ |
|
|
|
|
|
|
Πθ′+1(x-θ+1) = 1 – cθ′+1(x-θ+1) – |
Μθ |
dθ′(x-θ+1) = 0. |
|
|
|
|
|
|
|
|
|
|
µθ+1 |
|
|
|
Пусть x-θ = x-θ+1 = x-. Тогда |
|
|
|
|
|
|
|
|
Πθ′+1(x-) – Πθ′(x-) = cθ′+1(x-) – cθ′(x-) + |
Μθ |
dθ′(x-) – |
Μθ–1 |
dθ′–1(x-) = 0 |
|
|
µθ |
|
|
|
|
|
|
|
µθ+1 |
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Μθ |
– |
Μθ–1 |
Μθ–1 |
(dθ′(x)- |
– dθ′–1(x))- = 0. |
|
1 + |
µθ+1 |
dθ′(x)- + |
µθ |
|
|
|
µθ |
|
|
|
|
|
|
|
Поскольку |
Μθ |
> |
Μθ–1 |
|
|
|
|
|
|
|
|
µθ+1 |
µθ |
, dθ′(x-) > 0, и dθ′(x-) – dθ′–1(x-) >0, то левая часть положительна. Получили |
|
|
|
|
|
|
|
|
|
|
|
противоречие, т.е. x-θ ≠x-θ+1.
Модель найма с асимметричной информацией при монопольном положении нанимателя: общий случай
Предположим, что результат усилий x X работника — доход y~(x), представляющий собой случайную величину, распределение которой (Fx) зависит от x, но не зависит от типа (Fxθ = Fx θ). Будем считать, что ожидаемый доход y(x) = Ex y~(x) — монотонно возрастающая вогнутая функция уровня усилий, причем y(0) = 0.
Предположение о независимости распределения дохода от типа существенно упрощает анализ, поскольку в этом случае величина дохода не дает нанимателю информации о типе работника. При этом предположении естественно считать, что контракт — это функция только от усилий, но не от y~: w = w(x).
Наниматель имеет право претендовать на весь доход (за вычетом оплаты по контракту). Поэтому при данном уровне усилий x нейтральный к риску наниматель максимизирует ожидаемую прибыль
Ex(y~(x) – w(x)) = y(x) – w(x),
где w(x) — оплата уровня усилий x работника.
Пусть задано распределение вероятностей для типов работников. Например, в дискретном случае, описанном выше, оно определяется указанием вероятности µθ для работника каждого типа θ. Если работник типа θ осуществляет усилия xθ, то с точки зрения нанимателя усилия — это случайная величина. (В дискретном случае — это дискретная случайная величина, принимающая значение xθ с вероятностью µθ). Таким образом, выигрыш нанимателя равен следующей величине:
Eθ[Exθ(y~(xθ) – w(xθ))]
или, учитывая предположение независимости функции распределения дохода от типа работника,
Eθ[y(xθ) – w(xθ)].
Предполагаем, что функция полезности работника любого типа сепарабельна по деньгам и усилиям:

606
uθ(x, w) = vθ(w) – cθ(x),
где, как и выше, vθ(w) — полезность оплаты w, а cθ(x) — тягость усилий x для работника типа θ. Мы будем предполагать, что vθ(w) — возрастающая вогнутая функция, а cθ(x) — возрастающая выпуклая функция.
Разные типы работников характеризуются разной формой функций vθ(w) и cθ(x). Каждый тип работников характеризуется уровнем резервной полезности u0θ, заданной экзогенно.
Модель найма со скрытой информацией можно представить как динамическую игру с неполной информацией. Последовательность ходов в этой игре следующая:
0.«Природа» выбирает тип работника.
1.Наниматель, не зная типа, предлагает контракт w( ).
2.Работник (зная свой тип) решает, подписывать контракт или нет.
3.Если работник подписывает контракт, то он (зная свой тип) выбирает уровень усилий x.
4.«Природа» при данном x по распределению Fx случайным образом «генерирует» y~(x).
Природа
θ Θ
Наниматель w( )
|
|
Работник |
0 |
|
xθ |
u0 |
|
y~ Природа |
|
[Fx] |
|
|
y~(xθ) – w(xθ) |
|
vθ(w(xθ)) – cθ(xθ) |
Рисунок 144. Представление модели найма со скрытой информацией в виде дерева
Будем анализировать эту игру, используя обратную индукцию.
Уровень усилий xθ*, выбираемый работником типа θ, является решением задачи
vθ(w(x)) – cθ(x) → max x X .
В дальнейшем мы будем предполагать, что наниматель может выбирать только такие контракты, для которых эта задача имеет решение.

|
607 |
|
v(w(x)) |
|
c2(x) |
|
c1(x) |
|
x |
x2* |
x1* |
Рисунок 145. Выбор оптимальных действий работниками двух разных типов
Далее работник типа θ сравнивает значение этой задачи — уровень полезности, которую ему обеспечивает данный контракт, своей резервной полезностью и решает, подписывать ли ему контракт. Работник подписывает контракт, если
max x Xvθ(w(x)) – cθ(x) >u0θ.
Предположим, что vθ(w) = w226.
Это условие позволяют записать задачу работника в более простом виде:
w(x) – cθ(x) → max x X ,
где cθ(x) теперь обозначает величину cθ(x) + u0θ.
Поскольку ожидаемый доход y(x) — монотонная функция усилий, то можно измерять уровень усилий непосредственно величиной ожидаемого дохода. Таким образом, без ограничения общности будем считать, что уровень усилий измеряется величиной ожидаемого дохода, т.е. y(x) = x.
Обозначим через Iθ( ) индикаторную функцию, которая принимает значение 1, если условие в скобках выполнено, и 0 в противном случае.
В этих обозначениях задача нанимателя по выбору оптимального контракта имеет следующий вид:
EΠ= E[I(w(x) – cθ(x) >0)(xθ* – w(xθ*))] → max w( ) w(xθ*) – cθ(xθ*) >w(x) – cθ(x), x X, θ Θ,
В случае, если существует конечное число типов работников, можно решать эту задачу перебором. При этом выделяется подмножество типов работников, для которых выполнено ограничение участия. Для каждого такого подмножества решается эта задача, дополненная соответствующими ограничениями участия/неучастия и находится значение ожидаемой прибыли в максимуме. Затем находится то подмножество, для которого такая ожидаемая прибыль максимальна.
Если для рассматриваемых работников выполнено условие возрастания издержек по θ, —
cθ(x) >cϕ(x) ( x X) θ>ϕ, —
то перебор можно сократить, поскольку условия найма, выгодные для работников типа θ, окажутся таковыми и для работника типа ϕ при ϕ< θ, т.е.
226 Анализ в общем случае мы предлагаем читателю проделать самостоятельно.
Его можно провести двумя способами: несколько модифицировать анализ, проведенный в тексте или произвести соответствующую замену переменных.
608
w(x) – cθ(x) >0 w(x) – cϕ(x) >0.
Кроме того, из того, что работнику типа θ безразлично, подписывать контракт или нет, следует, что выполняется ограничение неучастия для работника типа ϕ при ϕ> θ, т.е.
w(x) – cθ(x) = 0 и ϕ> θ w(x) – cϕ(x) <0.
Из этих рассуждений следует, что можно рассматривать задачи, в которых подписывают контракт только работники с θ меньше некоторого порогового значения, причем ограничения неучастия для остальных типов работников можно не учитывать. Это позволяет без потери общности ограничится анализом случая, когда наниматель предлагает контракт, который выгодно подписать работнику любого типа, т.е. когда подмножество типов работников, для которых выполнено ограничение участия, совпадает со всем множеством Θ.
Проанализируем такой случай. Ему соответствует следующая задача:
EΠ= E(xθ* – w(xθ*)) → max w( )
w(xθ*) – cθ(xθ*) >w(x) – cθ(x), x X, θ Θ, w(xθ*) – cθ(xθ*) >0 , θ Θ.
Как и в модели с наблюдаемыми действиями, мы предполагаем, что работник выбирает те действия, которые выгодны нанимателю, поэтому можно считать, что наниматель сам выбирает усилия xθ*:
EΠ= E(xθ* – w(xθ*)) → max w( ), {xθ*} |
|
w(xθ*) – cθ(xθ*) >w(x) – cθ(x), x X, θ Θ, |
( ) |
w(xθ*) – cθ(xθ*) >0, θ Θ. |
|
Эта задача имеет бесконечно много решений. Для того чтобы охарактеризовать все ее решения, мы воспользуемся вспомогательной задачей, в которой рассматриваются только точки {xθ*}Θ и значения функции w( ) в этих точках. При этом в ограничении совместимости стимулов множество всех возможных действий X заменяется на множество {xθ*}Θ. Упростим обозначения: пусть xθ — усилия, которые, как планирует наниматель, должен осуществлять работник типа θ, а wθ — соответствующая зарплата. Пары (xθ, wθ) будем называть, как и выше, пакетами. Получаем следующую вспомогательную задачу поиска оптимальных пакетов:
EΠ= E(xθ – wθ) → max {wθ, xθ} wθ – cθ(xθ) >wϕ – cθ(xϕ), θ, ϕ Θ,
wθ – cθ(xθ) >0, θ Θ.
Выше мы проанализировали данную задачу.
Если издержки от усилий cθ( ) ведут себя неким регулярным образом в зависимости от θ, то рассматривая эту упрощенную задачу мы не теряем существенную информацию относительно оптимальных контрактов. На основе любого ее решение можно построить функцию w( ) так, что wθ = w(xθ) , θ Θ, причем w( ), {xθ}Θ составляют оптимальный контракт (обеспечивают максимум в задаче ( ) ). И наоборот, если w( ), {xθ}Θ — оптимальный контракт (решение задачи ( ) ), то соответствующие пары (w(xθ), xθ) являются решениями вспомогательной задачи.
Покажем, что любой набор оптимальных пакетов {w-θ, x-θ} можно реализовать как контракт (обуславливающий выбор работниками всех типов уровней усилий, соответствую-
609
щих заданиям «их» пакета). Простейший способ сделать это — реализовать данный набор пакетов как пакетный контракт, т.е. контракт следующего вида:
|
- |
-n |
|
w, |
x < x , |
w(x) = w-θ, x [x-θ, x-θ–1), θ> 1, |
|
|
x >x-1. |
w-1, |
где w- — достаточно малое число.
Заметим, что работнику типа θ при таком контракте выгодно выбрать усилия x-θ, гарантирующие оплату w-θ: любому x (x-ϕ, x-ϕ–1) он предпочитает x = x-ϕ, а x-θ для него не хуже x-ϕ.
- |
1 |
|
|
|
|
w |
|
|
|
|
|
|
|
c3(x) |
|
|
|
- |
2 |
|
|
|
|
w |
|
|
|
|
|
- |
3 |
|
|
|
|
w |
|
|
|
|
|
w- |
x- |
|
x- |
x |
|
x |
2 |
1 |
|
-3 |
|
|
Рисунок 146. Оптимальный пакетный контракт для 3 типов работников
Покажем, что этот контракт оптимален. Пусть это не так, то есть существует другой допустимый контракт w~( ), который обеспечивает нанимателю более высокую прибыль. Пусть при этом контракте работник типа θ выбирает усилия x~θ. Тогда пакеты {w~θ, x~θ}, где w~θ = w~(x~θ), являются допустимыми в задаче нахождения оптимальных пакетов ( ). Это противоречит оптимальности пакетов {w-θ, x-θ}.
Наоборот, любой оптимальный контракт w( ) и соответствующие ему уровни усилий
xθ* argmax{w(x) – cθ(x)}
определяют набор оптимальных пакетов {w(xθ*), xθ*}. Действительно, если эти пакеты неоптимальны, то существуют другие допустимые в задаче ( ) пакеты, обеспечивающие нанимателю большую прибыль. Однако эти альтернативные пакеты можно реализовать как пакетный контракт.
Вообще говоря, по данному набору оптимальных пакетов оптимальный контракт w( ) можно построить бесконечным числом способов. Требуется, чтобы функция w( ) проходила через точки (xθ, wθ), но не пересекала бы соответствующие кривые безразличия работников (лежала выше их).
Заметим, что функция w( ) будет иметь достаточно сложный вид. Например, если функции издержек дифференцируемы, то оптимальные пакеты нельзя реализовать в виде линейного контракта w(x) = a + bx: точки (xθ, wθ) могут не лежать на одной прямой, кроме того, при строгой выпуклости функций издержек кривые безразличия будут пересекать прямую, проходящую через эти точки даже и в том случае, если они лежат на одной прямой. Более того, как правило, оптимальный контракт не может быть гладкой функцией.
Задачи
26. Рассматривается стандартная задача выбора оптимального контракта с двумя неизвестными типами работников (производная издержек одного всюду выше производной
609

610
другого); предлагается два объема работы и два соответствующих уровня оплаты. Работник какого из типов выбирает уровень усилий более низкий, чем в случае, когда типы наблюдаемы?
27.Рассматривается стандартная задача выбора оптимального контракта с двумя неизвестными типами работников (производная издержек одного всюду выше производной другого); предлагается два объема работы и два соответствующих уровня оплаты. Работник какого из типов получит излишек полезности по сравнению с резервной полезностью?
28.Рассматривается стандартная задача выбора оптимального контракта с двумя неизвестными типами работников (производная издержек одного всюду выше производной другого); предлагается два объема работы и два соответствующих уровня оплаты. Работник какого из типов выбирает уровень усилий такой же, как и в случае, когда типы наблюдаемы?
29.В модели найма со скрытой информацией предположим, что издержки усилий работника типа t равны ct(x) = tx2, где t = 1, 2, и π1 = π2, где πt — доля работников типа t.
Определите характеристики контракта по найму этих двух типов работников (оптимальный уровень усилий, обусловленное контрактом вознаграждение для каждого типа работников).
30. В модели найма со скрытой информацией с двумя типами работников предположим, что издержки усилий работника 1-го типа равны c1(x) = x2, работника 2-го типа — c1(x) = αx2, причем доли работников обоих типов одинаковы.
Определите характеристики оптимального контракта.
31. В модели найма со скрытой информацией с двумя типами работников предположим, что издержки усилий работника 1-го типа равны c1(x) = x2, работника 2-го типа — c1(x) = 2x2.
Определите характеристики оптимального контракта в зависимости от доли работников первого типа.
32. В модели найма со скрытой информацией с двумя типами работников предположим, что издержки усилий работника 1-го типа равны c1(x) = x2, работника 2-го типа — c1(x) = 2x2, причем доли работников обоих типов одинаковы.
Определите характеристики оптимального контракта в зависимости от резервной полезности работников 1-го типа, в предположении, что резервная полезность работников 2-го типа равна нулю.
33. Заказчик нанимает подрядчика для производства некоторого блага. Ценность каждой единицы этого блага для заказчика равна 8. Подрядчик с вероятностью 1/3 может оказаться имеющим функцию полезности u1 = 12 + w – Q, и с вероятностью 2/3 — имеющим функцию полезности u2 = 5 + w – Q, где w — величина денежного дохода подрядчика, а Q
— это стоимость произведенных благ. Резервный уровень полезности подрядчика любого









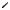 w-
w-









