Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Горные машины и оборудование

.pdf

Скачиваний:

296

Добавлен:

26.03.2016

Размер:

9.17 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1810 11 12 13 14 15 16 17 18 > Следующая >>>

где σz

и σу – проекции напряжения, действующего на гусеницу;

- нормальная к опорной поверхности нагрузка, действующая на опор-

ное основание со стороны гусеницы.

Однако энергия, подводимая к гусенице, тратится на преодоление всех

напряжений. Поэтому представление

fд

в виде суммы двух составляющих

отражает различный характер сил сопротивления деформации несущего ос-

нования.

4.4.4 Распределение давления на несущее основание

и его деформации

Давление, которое оказывает гусеничный движитель на несущееУосно-

вание, является его весьма важной характеристикой и, зачастую. Определяет

область его применения. Величина давления зависит как отТконструктивных

размеров гусеничного движителя, массы машины и других нагрузок, дей-

ствующих на машину. Среднее давление гусеничного движителя на несущее

основание

(4.84)

2a b

где Fz – проекция равнодействующей всех внешних сил на ось, перпендику-

лярную опорной поверхности.

Максимальные и минимальныеидавления определяют по формулам

(1.17). Входящие в эти ф рмулы м менты сопротивления опорной поверхно-

сти зависят от конс рук ивныхрсобенностей движителя: типа подвески

опорных катков,

числа, сп с ба соединения гусениц с рамой машины.

Рассмотрим на более распрос раненные жесткие одно- и двухопорные гусе-

ничные движители.

их

a/6

b3 3d 2

6 d b

Рисунок 4.17 – Ядро сечения основных типов гусеничных движителей:

а) - одноопорный движитель;

б) - двухопорный движитель

Для жесткого одноопорного движителя моменты сопротивления опорной площади с учетом того, что давление по ширине гусениц не меняется, определяются по формулам

I x

d b a3 d b a2

2 b

12 a / 2

;

ymax

(4.85)

2a b

d 2

I y

a b d

;

xmax

d / 2

где Ix и

- моменты инерции опорной площади относительно соответству-

ющих осей;

ymax = a/2, xmax = d/2

- максимальные координаты точек опорной площади.

M x

yд ;

(4.86)

M y

xд ,

где хд, уд - координаты цент а давлен я.

Имеем

3F y

F x

рz д z

pmax

p 1 6

a2 b

a b d

(4.87)

3F y

F x

тz

pmin

p 1 6

a b d

Приравняв к нулю последнее выражение, получим уравнение линии,

охватывающей ядро сечения жесткого одноопорного гусеничного хода

где

yд0

xд0

1 6

0 .

(4.88)

хд0, уд0

- координаты границы ядра сечения.

Это уравнение указывает на то, что ядро сечения ограничено прямыми

Рлиниям

представляет

собой

ромб

координатами

вершин

xд max

yд max

(Рис.4.17). При этом ядро сечения включает, как указывает проф.

Ф.А. Опейко, два отрезка прямых длиной

на осях гусениц.

У двухопорного жесткого гусеничного движителя давление изменяется как по длине, так и по ширине гусениц, а моменты сопротивления опорной площади (см.рис.4.17) равны

I x

d b a3

a2 b

;

ymax

12a / 2

(4.89)

I y

a d b 3 d b 3

a6 b2

xmax

12 d b / 2

3 d b

Воспользовавшись теперь формулами (1.17)

и учитывая (4.89),

запи-

шем условие равенства нулю минимального значения давления

3Fz yд

3Fz xд d b

2a b

a2 b

a b b2 3d

(4.90)

или

d b Б

Из этого соотношения заключаем, что контур ядра сечения ограничен

точкиb 3d

прямыми линиями и его

на осях Ох

Оу,

т. е. принимая попеременно

хд = 0 и уд

= 0, убеждаемся, что яд о сечения – ромб с вершинами на этих

осях. Максимальные и минимальныерзначения вершин ромба при этом равны

xд max

;

yд max

(4.91)

6 d b

Размеры и иформа ядра сечения для других конструктивных схем гусе-

ничных движителей приведены в работах [ ]. Следует заметить, что рас-

смотренные к нструктивные и приведенные в [

] схемы далеко не исчерпы-

таковые

вают все разновидности конструкций гусеничных движителей. Однако раз-

м ры и форма ядра сечения их опорных площадей, как правило, превышает

для других схем движителей.

Д формация несущих оснований под гусеничным движителем может быть рассчитана по зависимостям проф. Ф.А. Опейко, которые получены на основании формулы Герца. Для гусеничных машин эта зависимость имеет вид

h	p	3	a b	2	,	(4.92)
h			a b		,	(4.92)
г	Eг
	Eг

где hг – средняя деформация несущего основания под гусеницей; р – среднее давление по площади контакта.

Максимальная и минимальные деформации соответственно

pmax

3 a b2 ; h

pmin

a b2 ,

(4.93)

2 max

Eг

2 min

Eг

где pmax и pmin - максимальное и минимальное давления в пятне контакта.

4.4.5 Условия возможности прямолинейного движения

гусеничного движителя

Как и для горных машин на колесных движителях прямолинейное

движение машины на гусеничных движителях возможно при выполненииУ

двух основных условий:

- достаточности мощности;

- достаточности сцепления.

Первое из этих условий записывается точно так, как и для колесных

движителей

Nд

TT vT

(4.94)

Для записи второго

необходимо

разделить силы сопротивле-

1000

где N – мощность энергетическ х установок, передаваемая на гусеничный

движитель.

.4.18). условия

ния движению (

ния передвижению на

енние и внешние,

т.е. на силы сопротивления,

внут

действующие внутри гусеничнрго движителя, и внешние силы сопротивле-

рис

д pab

fк pab

k Tб

fд pab

1 Р3

1 mg sin

1 c1m dv

Рисунок 4.18 – Схема сил, действующих на гусеничный движитель при движении по прямой

При составлении этой схемы принято, что внешние силы сопротивления движению воспринимаются гусеницами поровну. Если теперь учесть место приложения сил сопротивления движению, то условие достаточности сцепления для гусеничного движителя можно записать в виде

2 f		p a b P	m g sin C	m	dv	2 f p a b ,	(4.95)
	д
		3	1		dt

где f – коэффициент сцепления (трения) между гусеницами и опорным основанием.

Для обеспечения прямолинейного движения гусеничной машины необходимо обязательное выполнение этих условий, хотя в конкретных ситуациях может потребоваться и соблюдение некоторых других ограничений (пре-

одоление брода, габаритное ограничение и т.д.).		У
4.4.6 Поворот гусеничной машины

Горные машины, особенно для подземных разработок, работают в
	Т
	Н

стесненных по габаритам условиях, что требует хороших маневренных качеств. Гусеничные движители, как уже отмечалось, удовлетворяют этим тре-

бованиям во многих случаях.		й

Рассматривая и устанавливая закономерности поворота, воспользуемся
теорией, разработанной проф. Ф.А. Опе ко и егоБучениками [ , , ]. Со-
	и
гласно этой теории гусеничная маш на рассматривается как механическая
корпус
система, состоящая из трех тел:		две гусеницы. Поворот осуществля-

ется за счет разных по величине ско остей перематывания гусениц и сопро-

скорос

вождается их скольжением по опо ной поверхности. При этом движение гу-

сениц относительно корпуса и д уг д уга – прямолинейно поступательное.

Если рассматривать пов

гусеничной машины на достаточно жестком

опорном основании,

.е. счи а ь движение опорных ветвей гусениц плоско-

параллельным, то план

ей при повороте гусеничной машины можно

представить следующей схемой (Рис.4.19).

еу

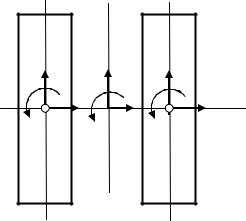
Рисунок 4.19 – Положение центров вращения опорных ветвей гусениц

и кинематика поворота

Для определения радиуса и угловой скорости поворота машины рассмотрим её движение как сложное, состоящее из переносного и относительного. За переносное движение примем движение опорных ветвей относи-

тельно поверхности грунта, а за относительное -

движение корпуса относи-

тельно опорных ветвей. На основании теоремы о сложении скоростей в

сложном движении запишем

r ,

(4.96)

где v – абсолютная скорость точек корпуса;

е - переносная (скорость скольжения цепей по залежи);

r - скорость корпуса относительно опорных ветвей гусеничных лент.

В точках С1 и С2 – центры вращения опорных ветвей гусеничных лент –

переносная скорость равна нулю. Поэтому для точек корпуса машины, сов-

падающих с точками С1 и С2, выражение (4.96) примет вид

1 r

(4.96)

Относительные скорости r1

r 2

корпуса равны скоростям перема-

тывания гусеничных лент

и u2,

х направление совпадает с осью Оу.

Таким образом, зная скорости лент

перематывания гусеничных це-

пей и смещения е1х ,

е1х ,

еу цент

в в ащения их опорных ветвей, мы знаем

скорости двух точек корпуса машины. Так как движение корпуса по условию

считать плоскопараллельным, это позволяет определить радиус и угловую

скорость поворота:

d u2

u2 e1x u1

e2x

2 u u

u u

;

(4.97)

u2 u1

где

R – радиус поворота,

за который принимается расстояние от центра С

вращ ния корпуса до его продольной оси; ω – угловая скорость поворота;

е1 и е2 - боковые смещения мгновенных центров вращения (мгновенных центров скоростей) опорных ветвей гусеничных лент относительно их продольных осей;

u1 , u2 - скорости перематывания гусениц относительно корпуса;

d- поперечная база движителя.

Линия, на которой расположены центры вращения опорных ветвей гу-

сениц, остается перпендикулярной продольной оси машины и смещается относительно центра симметрии на некоторое расстояние еу. Это положение

проф.Ф.А. Опейко доказал в математической теории трения [

]. Действи-

тельно, выражая проекцию скорости какой-либо точки корпуса на ось Ох ис-

пользуя (4. ) и взяв за переносные скорости скорости центров вращения

опорных ветвей гусениц запишем

ex rx 0 y yC ,

(4.96)

где у

- координата рассматриваемой точки;

- продольная координата центра вращения.

Так как записанное соотношение справедливо для уС1

и уС2 ,

то уС1 = уС2 = еу, что и требовалось доказать.

еу Умогут быть

Координаты центров вращения или их смещения е1,

е2,

найдены из уравнений равновесия гусеничной машины при совершении по-

ворота. Рассматривая статический поворот, т.е. равномерныйТповорот гусе-

ничной машины без учёта сил инерции, эти уравнения (Рис.4.

) можно пред-

ставить в виде

йТ

1у

Ру

2у

Т1х

Рх L

Т2х

Р сунок 4.20 – К составлению уравнений равновесия

гусеничного

движителя при совершении поворота

Px T1x T2x 0,

Py T1y

T2 y 0,

(4.97)

M L1 L2 0,

Рх

– проекция равнодействующей внешних сил на ось Ох;

– то же самое на ось Оу;

где

М – главный момент внешних сил относительно начала координат;

Т1х ,

Т2х , Т1у , Т2у - проекции равнодействующей сил трения между гусе-

ницами и грунтом на соответствующие оси;

L1 – моменты этих сил относительно геометрических центров гусе-

ниц.

Как проекции Т1х ,

Т2х ,

Т1у ,

Т2у , так и моменты L1

выражаются

интегралами

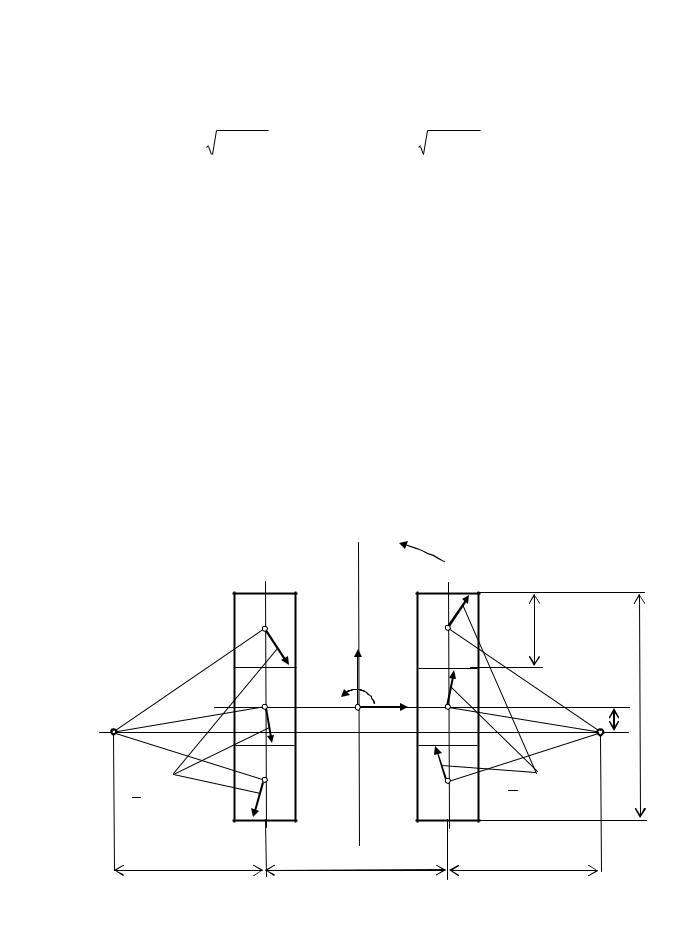
T1x dT1x ;

T2x dT2x ;

T1y dT1y ;

T2 y dT2 y

L1 dL1 ;

L2 dL2 ,

(4.98)

где dT1 f p1 dS1 ;

dT2 f p2

dS2 ;

dL f p dS

y 2

;

dL f p

y 2

а интегрирование ведется по площадям S1 и S2

опорных площадок гусениц.

Вычисление этих интегралов приводит к очень громоздким выражени-

ям. Их качественное поведение изучено в работах [

, , ].

В связи с этим, в свое время были предложены упрощенные схемы гу-

сеничной машины в состоянии поворота, а также приближённые методы ре-

шения системы уравнений равновесия. Упрощения заключаются в замене

распределенных по опорным площадкам элементарных сил трения сосредо-

точенными силами, приложенными в некоторых характерных точках опор-

ных площадок гусениц. Автор наиболее распространенной теории поворота

гусеничных машин Ф.А. Опейко предложил приложить сосредоточенные си-

лы трения в геометрических центрах половин опорных площадок гусениц,

что позволило найти решение уравнен

равновесия относительно смещений

центров вращения в некоторых частныхйслучаях и на их основе построить

численные способы решения [

]. Точные решения упрощённых уравнений

равновесия можно найти также п и азбиении опорных площадей гусениц на

три части и приложении с с ед т ченных сил трения в геометрических цен-

трах (Рис.4.

) получаемых при

ак м разбиении площадок [

а/3

Ру

Рх

еу

С1

С2

1 f1 p1ab

3 f2 p2 ab

е1

е2

Рисунок 4.21 – К составлению уравнений равновесия

при разбиении опорных площадей гусениц на три равнее части

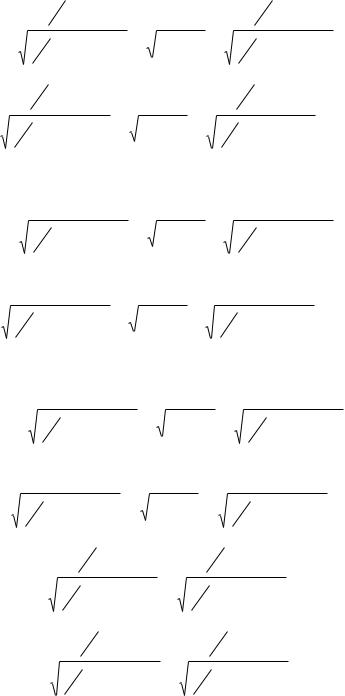
Тогда уравнения равновесия имеют вид

fp ab

3 ey

;

a 3 ey

2 ab

																																																																			Т;
																																																																							У
		Py					fp ab																e																				e																	e
		Py							1															1																				1																		1
									1															1																				1																		1
									3							a												2							2							2				2								a												2			2
																a			e y												e1										e y			e1										a		3		e y									e1
																	3		e y												e1																									3		e y									e1
																																																Б
																																																Б
				fp			ab											e																						e																	e
						2													2																							2																	2										0
																																																									Н
						3							a																																						a						Н
																	e						2			e 2												2						2											e						2			e 2
															3		e			y						e 2												e y				e2										3			e				y					e 2
															3					y											2																					3							y								2
																															и																																									(4.99)
																															и
					d			fp				ab												e																					e																			e
																					р
		M									2																2																			2																			2
					2						3						a													2						2		й2 2																	a												2			2
																	a					e						y					e			2							ey			e2									a			3		e						y		e		2
																		3										y								2																						3								y				2
														о
			d dfp ab																	e																							e																e
							1															1																				1																		1
							1															1																				1																		1
			2				3							a				e								2				e				2								2				2						a					e							2			e		2
			2				3																			2								2								2				2																		2					2
																	3						y																	ey e1															3						y
																	3						y										1																						3						y							1
		з
		з								тa fp ab															a						ey																	a				ey
										тa fp ab																		3			ey																				3	ey
													1															3																							3
							3													a																										a
							3						3															e							2	e			2											e						2		e				2
				и																								e				y				e														e			y					e
	п			и																			3									y						1								3							y								1
	п																									a					ey																		a			ey
																										a					ey																		a			ey
										a		fp2 ab																	3																						3																0

										3			3									е2,								еу					2					2																2							2
сительно трех неизвестных е1,																						е2,								еу					только численными способами. Вместе
	о																				a			3				e					y				e			2							a	3			e			y				e					2
Р																								3									y							2								3						y									2
Р	В общем случае эта система уравнений (4.99) может быть решена отно-

с тем точное решение может быть найдено для простейшего случая статического поворота, под которым понимается поворот при отсутствии внешних сдвигающих сил и равномерном распределении давления под гусеницами, т.е. при Рх = Ру = 0, М = 0, Р1 = Р2 = 0. При таких условиях из первых двух уравнений системы (4. ) следует, что е1 = е2, еу = 0. Обозначив, в этом случае. Равные боковые смещения центров вращения опорных ветвей гусениц через е0 получим третье уравнение в виде

									a
						2			a
		2e0			a	2		3
d				1								0 .	(4.100)
d		2		1	3						2	0 .	(4.100)
	a	2			3	2				a	2
	a	2				2				a
			e0				e0
	9		e0				e0			9
	9									9

Это уравнение преобразуется к квадратному относительно е0

3е2

16a2

16a4

9a2 d 2

0 ,

(4.101)

81d 2

а его решение

8a2 a 16a

2 27d 2

(4.102)

27d

Это решение дает значения несколько меньше, чем по формуле (4.99)

a 2

(4.103)

Но, самое главное

отличие

ешен я (4.102) от решения Ф.А. Опейко

состоит в том, что оно определяет

исновные параметры гусеничной машины,

цент

(4.104)

при которых е0 =0, т. е.

ы в ащения находятся на продольных осях гу-

сеницы., а поворот машины пр исх дит вокруг центра остановленной гусе-

при

ницы. Это достигае ся

в условиях пр стейшего случая поворота.

Ф рмула (4.103) находится решением уравнения

8a2 a

16a2 27d 2

0 .

(4.105)

пПри сравнительно небольших значениях Рх, Ру, М решение системы

(4.99) можно найти по формулам

16d 2

a 2

e1 e0 e1 ;

e2 e0

e2 ;

(4.106)

16 p b

где е1, е2 - поправки решения, которые предложил проф. Ф.А. Опейко используя приближённое решение по методу Ньютона. Поправки е1 и е2 находятся по формулам

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1810 11 12 13 14 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
02.09.201954.13 Кб1Глава двадцать вторая.docx
#
08.12.20181.37 Mб6голованова н.в..docx
#
31.05.201515.97 Кб26ГОЛОДАНИЕ ПО ОГАНЯН.docx
#
31.05.2015163.2 Кб13голу.docx
#
26.09.20195.59 Mб3Голубков МИ.doc
#
26.03.20169.17 Mб296Горные машины и оборудование.pdf
#
31.05.201589.12 Кб16Горные породы.docx
#
22.09.2019994.82 Кб13ГОС (шпоры).doc
#
20.08.201964.03 Кб5ГОС шпора Психология печать.docx
#
07.05.2019183.3 Кб3Госбилеты-12.doc
#
25.08.2019112.81 Кб2ГОСТ 2.004-88 Общ треб к вып констр и техн док....docx