Транспонированная матрица

Если в матрице 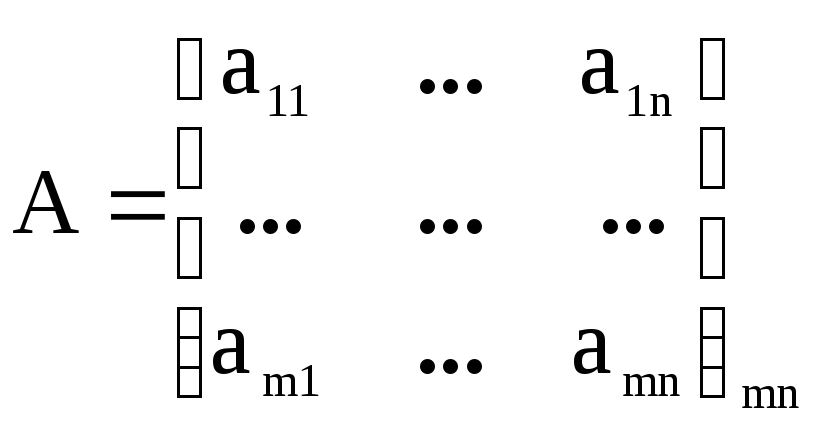строки и столбцы поменять местами, то получим транспонированную матрицу.

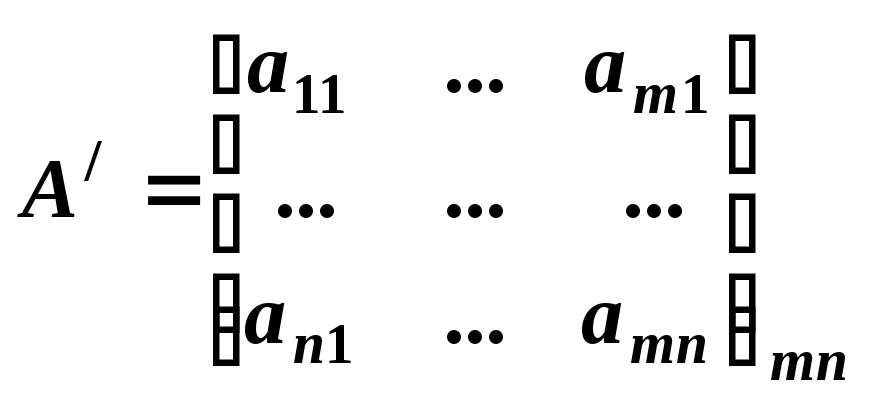
Свойства:

1. дважды транспонированная матрица равна исходной

А^{‌ ‌}= (А^‌ )^‌= А;

2. (А+В)^‌ =А^‌+ В^‌;

3. (АВ)^‌ =В^‌А^‌, т.е. (АВ)^‌ ≠ А^‌В^‌;

4. Если А^‌=А, то матрица А^‌- симметричная

(а_ij=a_ji)

Обратная матрица

Обратной матрицей по отношению к данной квадратной, называется матрица, которая, будучи умноженной как справа, так и слева на данную матрицу, дает единичную матрицу. Обозначим для матрица А обратную ей матрицу через А^-1.

АА^-1=А^-1А=Е.

Нахождение обратной матрицы для данной называется обращением данной матрицы.

Квадратная матрица называется неособенной, если ее определитель не равен нулю, в противном случае матрица называется особенной или сингулярной. Обратная матрица имеет только у неособенной матрицы.

Пусть имеем матричное равенство

АС=В.

Умножим правую и левую часть равенства на обратную матрицу А^-1

А^-1АС= А^-1В.

Поскольку известно, что А^-1А=Е, то

ЕС= А^-1В.

И поскольку известно, что ЕС=С, то

С= А^-1В.

То есть, мы равенство АС=В преобразовали в равенство С= А^-1В, выразив матрицу С.

Если бы у нас были простые алгебраические числа а, bи с, то аналогичные преобразования были бы следующие:.

Сравнив преобразования для алгебраических чисел и матриц видим, что обращение матрицы соответствует действию деления. Поэтому понятна необходимость в обратной матрице, в ее вычислениях.

Алгоритм получения обратной матрицы

1. Вычисление det A;

2. Транспонирование матрицы ;

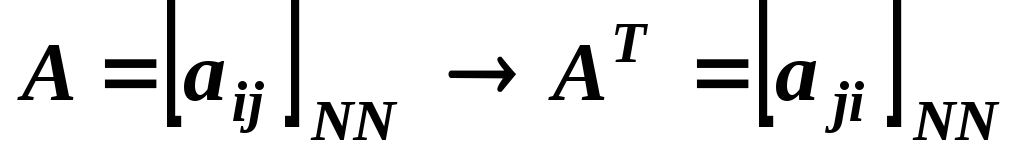3. Определение алгебраических дополнений А_ji,j=1,N;i=1,N;

4. Составление союзной матрицы ;

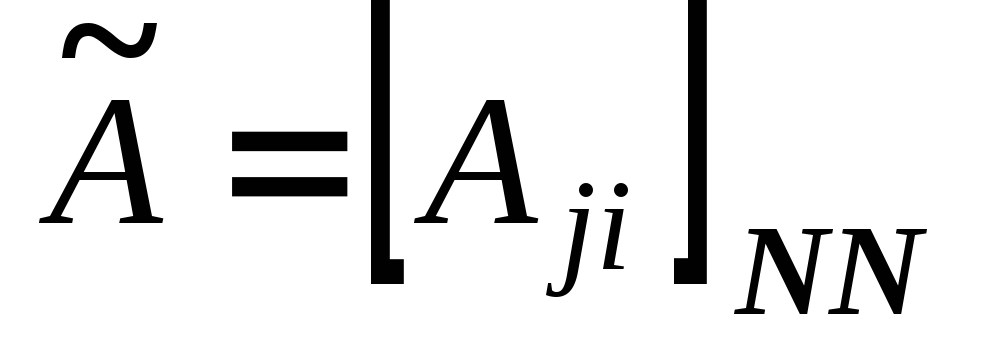5. Вычисление обратной матрицы

;

6. Проверка А^-1А=Е.

Существуют другие, более удобные способы вычисления обратной матрицы, например, методом Жордана – Гаусса, с которым познакомимся позднее.

Классический метод получения обратной матрицы

Пусть данная матрица:

.

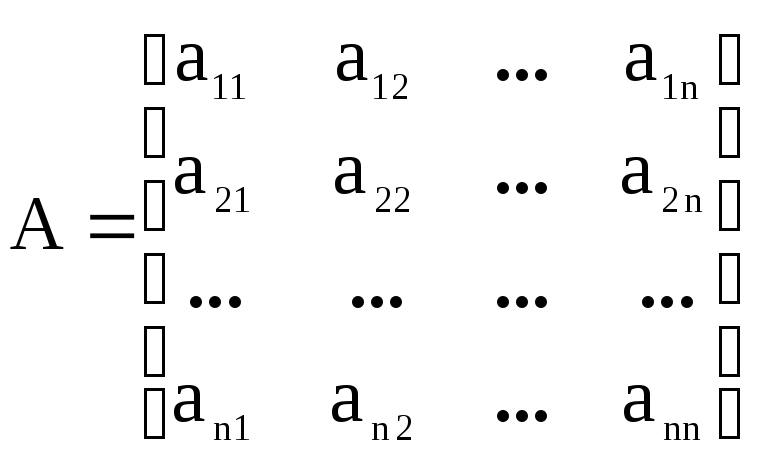Транспортируем ее .

Найдем для каждого элемента а_jiтранспортированной матрицыА^Талгебраические дополненияА_ji.

Теперь составим для матрицы А так называемую присоединенную (или союзную) матрицу

.

Обратная матрица будет равна

.

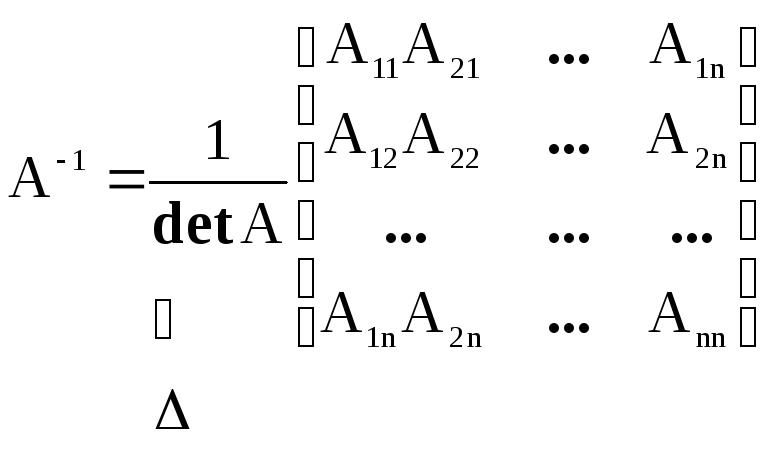Например: найти обратную матрицу для матрицы третьего порядка.

.

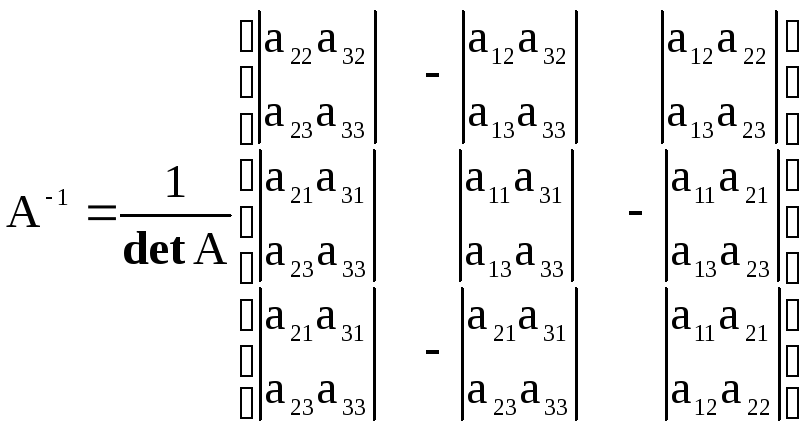Основные свойства обратной матрицы

1. Учитывая, что det(AB)=detA∙ detB,можем записатьdetA^-1 detA=detE=1.

Отсюда

.

Определитель обратной матрицы равен обратной величине определителя исходной матрицы.

2. (АВ)^-1=В^-1А^-1

3. (А^-1)=(A¹)^-1.

Тема 2.1. Теория графов в электроэнергетике

Некоторые сведения об электрических системах

Следует иметь в виду, что предлагаемая дисциплина читается до изучения основных курсов по специальности 140204 (100100). Поэтому для того, чтобы приблизить излагаемый материал не только по содержанию, но и по форме к будущим специальным курсам, вспомним некоторые понятия, уже знакомые по курсу “Введение в специальность”.

Рис.1. Принципиальная схема энергосистемы

Энергетическая системаначинается с топлива и воды и кончается потребителем (рис.1).

Электрическая системаначинается с генератора и кончается потребителем, т.е. электрическая система – это электрическая часть энергетической системы, состоящая из совокупности элементов, вырабатывающих, преобразующих, передающих, распределяющих и потребляющих электроэнергию.

Электрическая сетьначинается с повышающего трансформатора и кончается потребителем.

Работа электрической системы прежде всего характеризуется значениями мощностей в МВт (и энергии в МВт.час), вырабатываемых, преобразуемых, передаваемых и потребляемых всеми ее элементами.

Режим системы– это ее состояние в любой момент времени, которое характеризуется совокупностью параметров.

Параметры режима– это напряжение в различных точках системы, токи в ее элементах, углы расхождения векторов ЭДС и напряжений, активные и реактивные мощности генераторов, потоки активной и реактивной мощности в линиях и трансформаторах, потери мощности, энергии и напряжения в элементах системы и т.д.

При анализе различают два основных вида режимов электросистем:

1. установившийся режим (нормальный или послеаварийный) ;

2. переходный режим (нормальный или аварийный ).

Установившиеся режимы в электрической системе описываются законами Ома и Кирхгофа или вытекающими из них уравнениями узловых напряжений и контурных токов. Математический анализ установившихся режимов работы электрических систем сводится к составлению и решению систем линейных и нелинейных уравнений. Переходные процессы электрических систем описываются системами дифференциальных уравнений. Наиболее широко применяемые при анализе режимов электрических систем методы решения линейных, нелинейных и дифференциальных уравнений будут изложены во втором разделе данного курса.

Электрической схемой системыназывается графическое изображение последовательности соединения ее элементов между собой. Элементы электрической системы обладают активными и реактивными (индуктивными или емкостными) сопротивлениями, активной и реактивной (индуктивной или емкостной) проводимостями. Если заменить в электрической схеме элементы системы их сопротивлениями и проводимостями, то получим схему замещения электрической системы. Расчеты и анализ режимов электрической системы производятся на основе ее схемы замещения. Каждый элемент системы имеет свою схему замещения. ЛЭП 110 - 220 кВ обычно представляются П -образной схемой замещения, а двухобмоточный трансформатор – Г-образной. на рис.1 и 2 приведены соответственно электрическая схема сети и ее схема замещения.

Рис.2. Электрическая схема сети

Рис.3. Схема замещения

Перед тем, как начать рассчитывать режим работы электрической системы (т.е. определять параметры режима) составляют схему замещения электрической системы (или сети) и вычисляют все параметры схемы замещения – сопротивления и проводимости. Электрическая схема сети и ее схема замещения, представленные на рис.1 и 2, очень малы, и рассчитать режимы для такой схемы можно “вручную”. Однако реальные электрические системы достигают больших размеров, их схемы замещения очень сложны и без использования современных ЭВМ выполнить анализ режимов электрических систем невозможно. Использование же ЭВМ для указанной цели основано на применении матричной алгебры и теории графов.