Метод простой итерации

Дана система линейных уравнений

Предположим, что диагональные элементы а_ii,i = 1-nне равны 0. В любом случае строки и столбцы можно поменять местами так, чтобы диагональные элементы не были равны 0. Разделим каждую строку на ее диагональный элемент: первую строку на, вторую строку наи т.д. Получим следующую систему

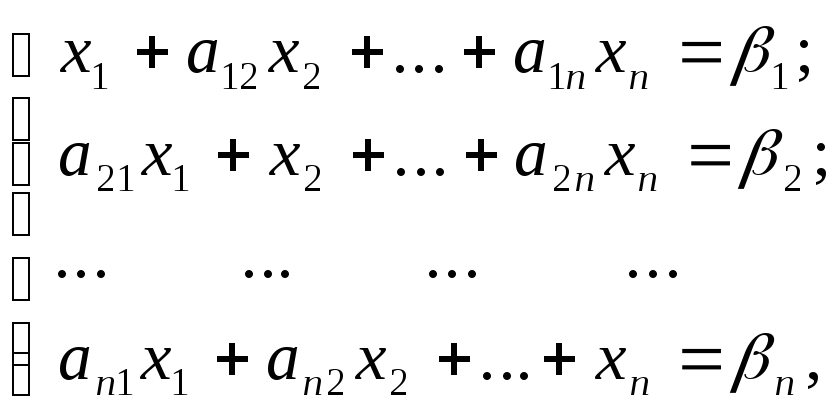
где ;.

В матричном виде эту систему можно записать

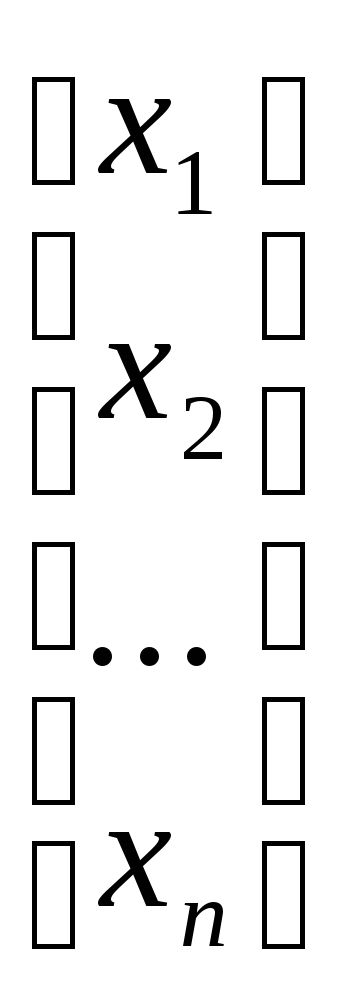
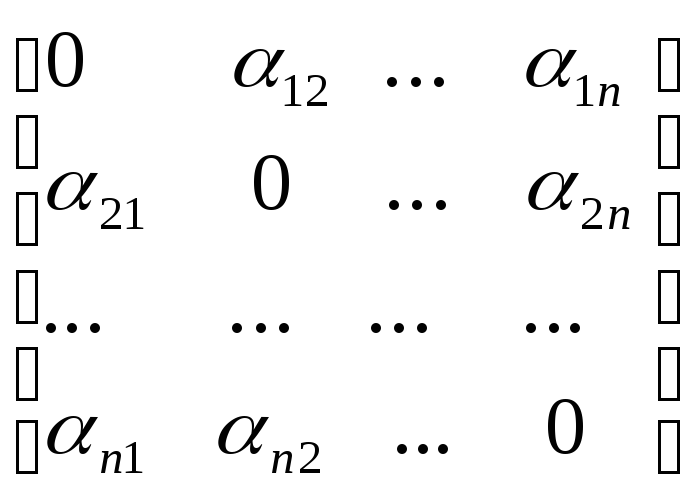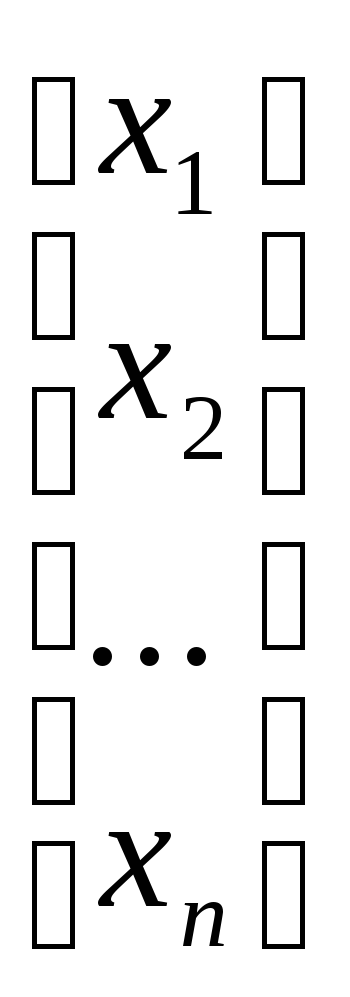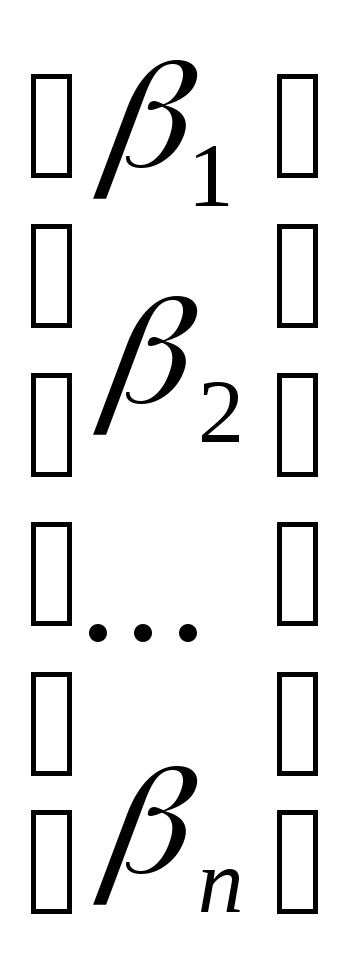+ х=или.

Отсюда . (1)

Выполненная выше операция называется приведением системы линейных уравнений к виду, удобному для итераций.

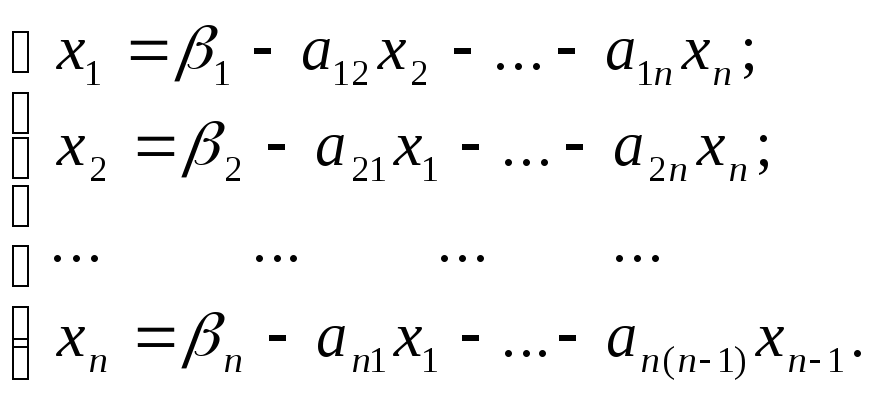
Зададим произвольное начальное значение всех неизвестных корней системы (в матричном видеХ=Х⁽⁰⁾)и подставим это значение в правую часть системы уравнений (1).

Вычислим ,

где Х⁽⁰⁾– начальное (исходное) приближение к корням системы уравнений,

Х⁽¹⁾- первое приближение к корням системы уравнений.

Затем процесс повторим, подставив найденные на первой итерации значения Х=Х⁽¹⁾в правую часть системы уравнений и вычислим вторые приближения корней

. И так далее.

Итерационный процесс повторяем до тех пор, пока на какой-нибудь к-й итерации не выполнится условие

<ε,

где ε – заданная точность определения корней системы.

Поскольку в вектор Хвходитnнеизвестных, то условие окончания итерационного процесса, должно быть выполнено для всехnкорней.

Пример: дана система линейных уравнений

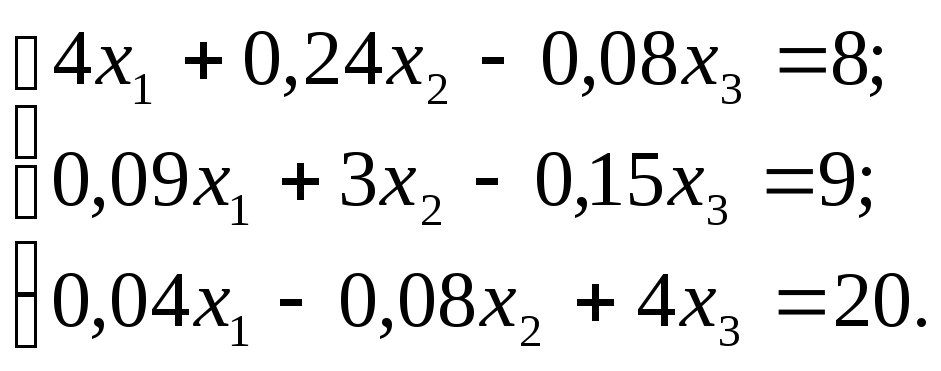
Приведем систему уравнений к виду, удобному для итерации

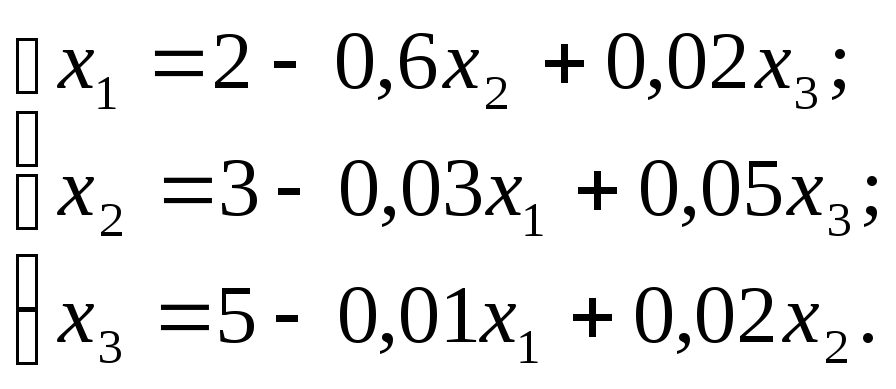
Зададим начальные приближения к корням равными нулю и точность расчета ε = 0,001.

Начнем итерационный процесс вычисления корней.

1итерация

2итерация

и т.д. до выполнения условий

Вычисления сведем в таблицу

№ итерации (к)
0	0	0	0
1	2	3	5
2	1,92	3,19	5,04
3	1,9094	3,1944	5,0446
4	1,9092	3,1949	5,0448

Примечание: число цифр после запятой в вычисляемых приближениях к корням надо брать на один порядок больше чем в заданной точности ε.

Достаточное (но не необходимое) условие сходимости итерационного процесса

Итерационный процесс будет сходящимся, если модуль коэффициента на главной диагонали больше суммы (или равен сумме) модулей остальных элементов строки (свободные члены при этом не учитываются)

Это достаточное условие сходимости, но не необходимое, т.е. данное условие гарантирует сходимость итерационного процесса. Условие не является чрезмерным в электрических системах оно часто выполняется, в том числе для матриц узловых проводимостей Y_у при решении систем узловых уравненийY_iU_у=I_уи контурных сопротивленийZ_кпри решении системы контурных уравненийZ_кI_к=.

Итерационный процесс сходится значительно быстрее, если диагональные элементы матрицы Азначительно больше недиагональных элементов. Этого можно добиться меняя строки и столбцы местами, при этом оставляя систему линейных уравнений неизменной относительно значений корней.

Пример: 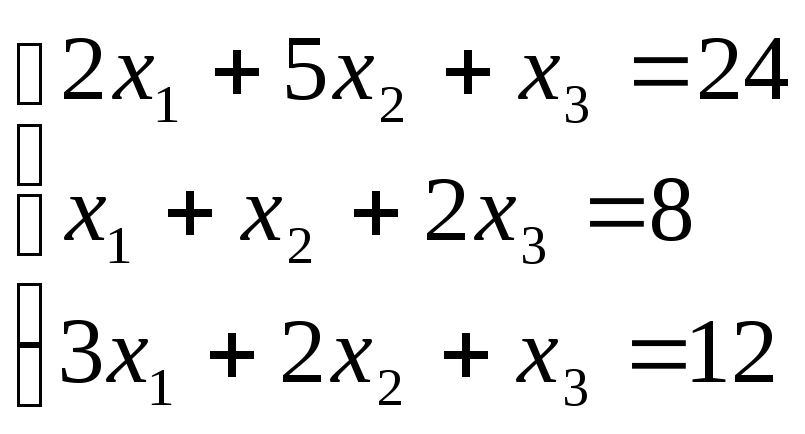Условие сходимости не выполняется

Поменяем строки местами

Условие сходимости выполняется.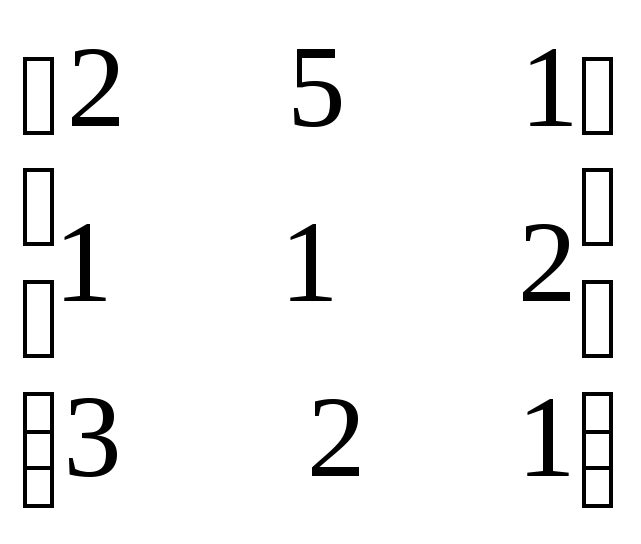

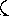
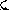
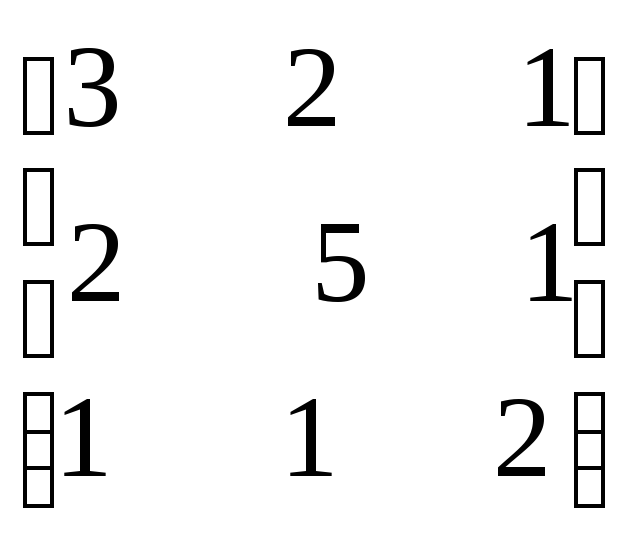, т.е.

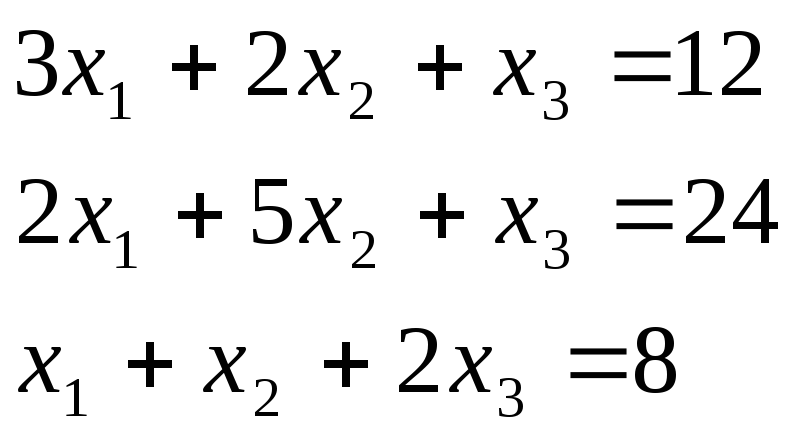
Или поменяем столбцы местами

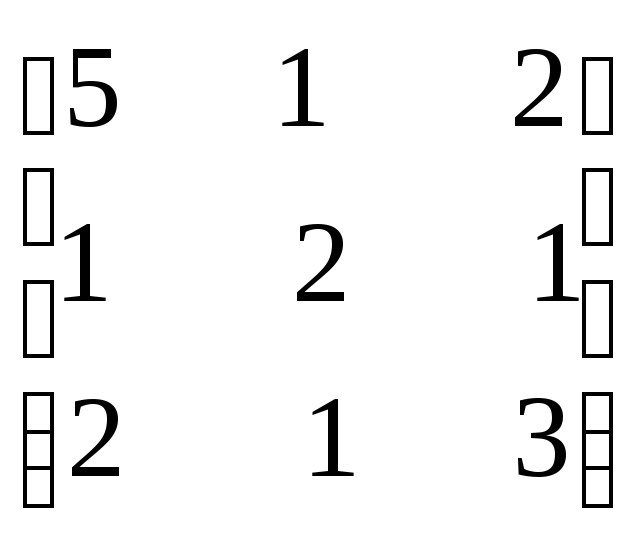, т.е.

Условие сходимости также выполняется.

Метод итерации обладает таким важным свойством, как самоисправление арифметических ошибок. Можно доказать, что если вычислительный процесс сходится при х⁽⁰⁾, то он будет сходится и при другом приближении, которое вычислено с ошибкой. При ошибке у нас только изменится число итераций.