- •Федеральное агентство по образованию
- •Определитель
- •Миноры и алгебраические дополнения
- •Второй способ вычисления определителя
- •Третий способ вычисления определителя
- •Действия с матрицами
- •Транспонированная матрица
- •Обратная матрица
- •Алгоритм получения обратной матрицы
- •2.2 Геометрический образ электрической сети
- •2.3. Уравнения законов Ома и Кирхгофа в матричной форме
- •2.4. “Прямой ” расчет токораспределения в электрической сети
- •2.5. Метод узловых напряжений для расчета токораспределения
- •2.6. Метод контурных токов [л-4, с.25-228]
- •Раздел 2. Методы решения систем алгебраических уравнений
- •Тема 2.I методы решения систем линейных уравнений
- •Метод обратной матрицы
- •Метод Крамера
- •Метод Гаусса
- •Метод простой итерации
- •Достаточное (но не необходимое) условие сходимости итерационного процесса
- •Метод Зейделя
- •Преимущества и недостатки итерационных методов
- •Тема 2.2 решение систем нелинейных уравнений Понятие о системах нелинейных уравнений и методах их решения
- •Решение нелинейного уравнения методом Ньютона
- •Решение системы нелинейных уравнений методом Ньютона
Раздел 2. Методы решения систем алгебраических уравнений
Тема 2.I методы решения систем линейных уравнений
Методы решения систем линейных алгебраических уравнений разделяются на точные и итерационные. Точные методы представляют собой конечные алгоритмы для вычисления корней системы. Это - метод обратной матрицы, метод Крамера, метод Гаусса, метод Жордана-Гаусса, метод главных элементов, метод квадратных корней и др. Несмотря на то, что методы называются точными, результаты вычислений имеют погрешности вследствие неизбежных округлений при выполнении действий.
Итерационные методы позволяют получать корни системы с заданной точностью путем сходящихся бесконечных процессов. К их числу относятся: метод простой итерации, метод Зейделя, метод релаксации и др. Эффективность применения итерационных методов существенно зависят от удачного выбора начального приближения и быстроты сходимости процесса.
Все вышеперечисленные методы (точные и приближенные) имеют свои преимущества и недостатки и поэтому для выбора оптимального (лучшего) метода для решения конкретной системы линейных уравнений требуются знания пользователя.
А. Пусть дана система nлинейных уравнений сnнеизвестными
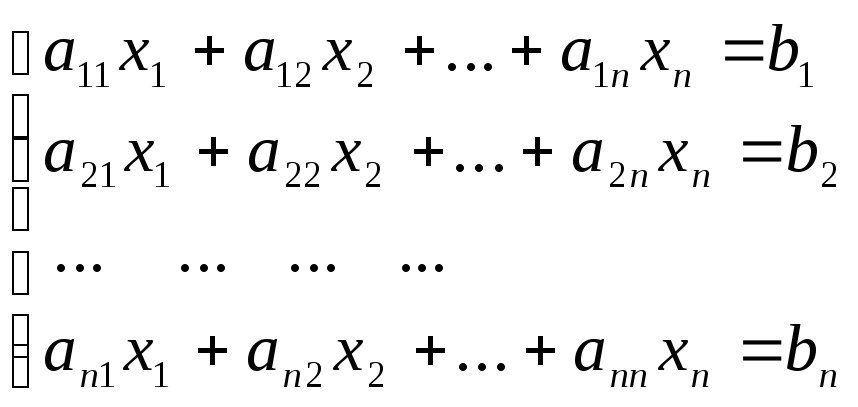
Запишем эту систему в матричном виде
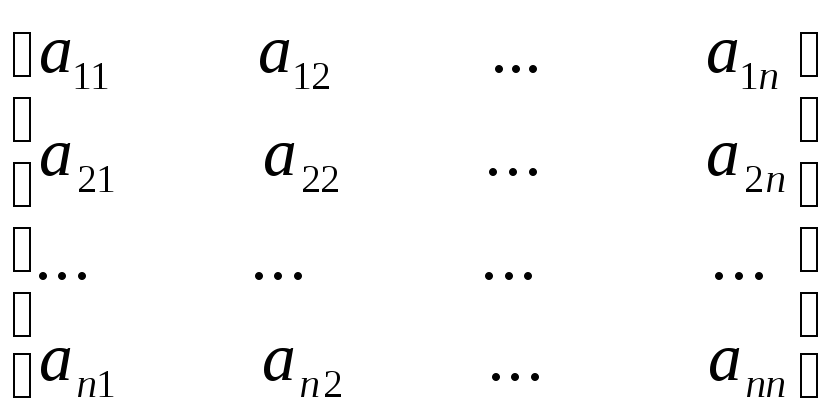 х
х
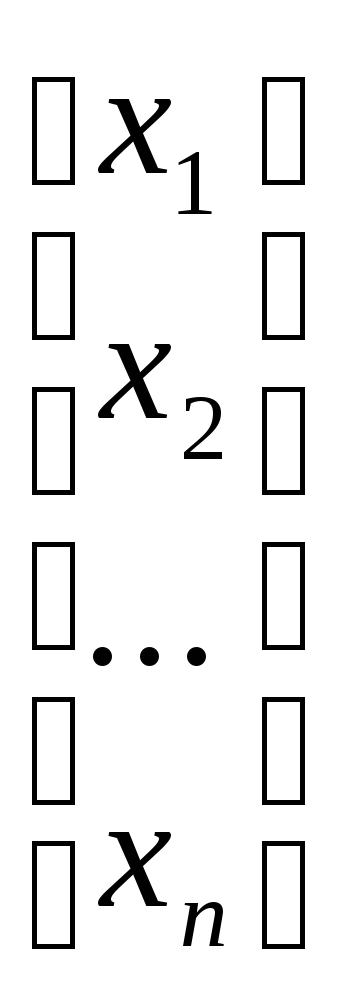 =
=
или в общем матричном виде
А∙Х=В,
где: А- матрица коэффициентов;
Х– вектор искомых параметров;
В– вектор свободных членов.
Рассмотрим решение линейной системы уравнений различными методами.
Метод обратной матрицы
Дана система линейных уравнений
А∙Х=В.
Умножим правую и левую части системы на обратную матрицу А-1
А-1∙А∙Х= А-1∙В
Так как А-1∙А=Е,тоЕ∙Х= А-1∙В ЕХ=Х
Так как ЕХ=Хто,Х= А-1∙В.
Таким образом данный метод заключается в нахождении обратной матрицы коэффициентов А-1и ее умножении на вектор свободных членов В. Нахождение обратной матрицыА-1при порядкеn>4 требует много времени, поэтому метод обратной матрицы редко употребляется.
Метод Крамера
Известно, что
![]() .
.
Отсюда
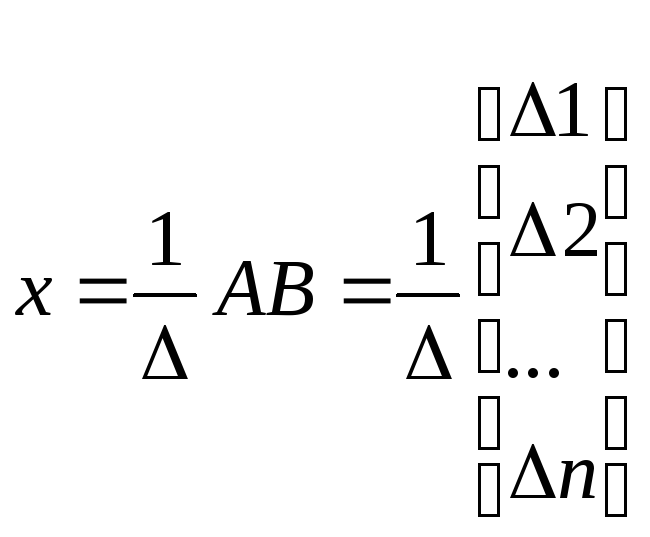 ,
,
где ![]() ,
,
![]() ,
…,
,
…, ![]()
где

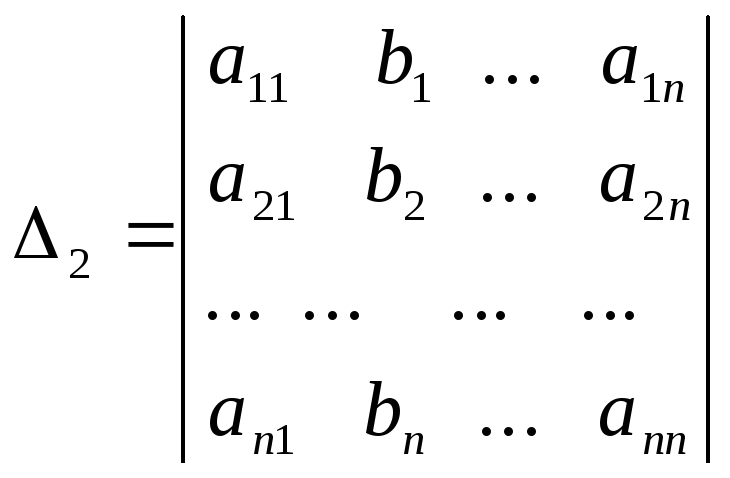
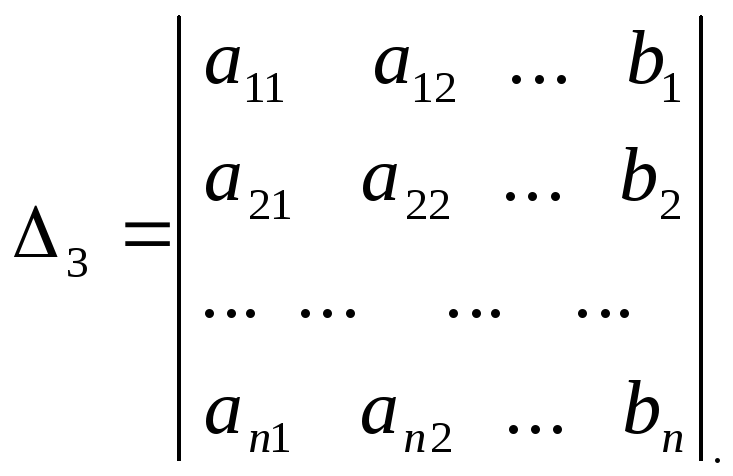
Итак, метод Крамера заключается в вычислении (n+1)-го определителя (∆1, ∆2, ∆3, …, ∆n) для матрицn-го порядка. Если число велико, то вычисление определителей является трудоемкой задачей.
Наиболее распространенным способом решения системы линейных уравнений является метод последовательного исключения неизвестных или метод Гаусса.
Метод Гаусса
Рассмотрим на простейшем примере известный со школы способ исключения неизвестных при решении систем уравнений. Пусть дана система:
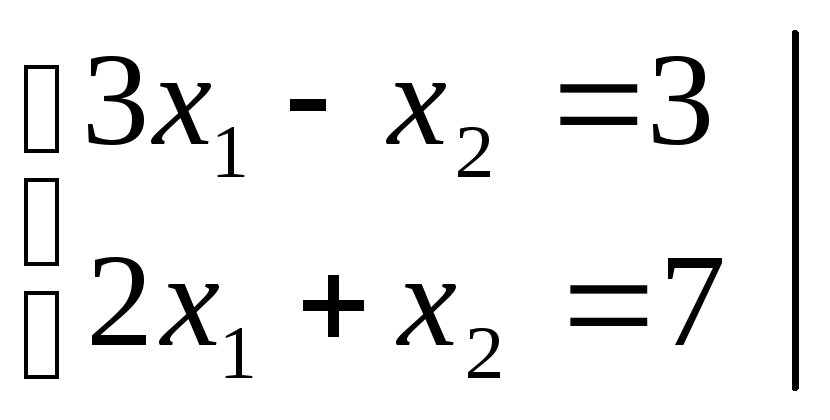
![]()
Умножим
первое уравнение на такой коэффициент
![]() ,
чтобы в обоих уравнениях коэффициент
прих1стал бы одинаковым
,
чтобы в обоих уравнениях коэффициент
прих1стал бы одинаковым
![]()
![]()
Теперь вычтем его из второго уравнения, т.е.
-2х1+х2=7
![]()
![]()
Мы выполнили операцию исключения неизвестной х1 из второго уравнения. Запишем систему уравнения после этого исключения в следующем виде. Первое уравнение записываем в исходном виде.

Второе уравнение содержит лишь одно неизвестное, которое легко вычисляется х2=3. Подставив полученное значениех2в первое уравнение, можем вычислить и первое неизвестноех1.
Проведенные действия и составляют сущность метода Гаусса. Рассмотрим преобразования по методу Гаусса для системы уравнений n-го порядка.
|
а11х1+ а12х2+ … +а1nхn=b1 |
х |
|
|
|
|
|
а21х1+ а22х2+ … +а2nхn=b2 |
|
|
|
|
|
|
а31х1+ а32х2+ … +а3nхn=b3 |
|
|
|
|
|
|
… … … … |
|
|
|
|
|
|
аn1х1+ аn2х2+ … +аnnхn=bn |
|
|
|
|
|
Вычтем
из второго уравнения первое, умноженное
на
![]() .
.
При этом во втором уравнении будет уничтожен коэффициент при х1.
Затем
из третьего уравнения также вычтем
первое, умноженное на
![]() .
.
Проделав аналогичные преобразования с остальными уравнениями системы, превратим в нуль все коэффициенты первого столбца, кроме элемента а11. Получим следующую систему:
|
а11х1+ а12х2+ а13х3+… +а1nхn=b1 |
|
… |
|
|
|
|
| |
|
|
|
|
|
|
… … … … |
|
|
|
|
|
|
|
|
Затем при помощи
второго уравнения преображенной системы
исключим из третьего, четвертого и т.д.
уравнений коэффициенты второго столбца
лежащие ниже
![]()
а11х1+ а12х2+ а13х3+… +а1nхn=b1
![]()
![]()
… … …
![]()
Последовательно продолжая этот процесс, исключим из системы все коэффициенты, лежащие ниже главной диагонали. В результате получим треугольную систему уравнений.
а11х1+ а12х2+а13х3+… +а1nхn=b1
![]()
![]()
… … …
![]()
Процесс получения
треугольной системы называется “прямым
ходом” по методу Гаусса. Треугольная
система легко решается “обратным
ходом”. Из последнего уравнения
определяется последнее неизвестное
![]() .
Затем из предпоследнего уравнения
постановкой найденного значенияхnопределяетсяхn-1.
После решения системы уравнений методом
Гаусса необходимо делать проверку,
подставляя в исходные уравнения найденные
значения переменных хi(i= 1, …,n).
.
Затем из предпоследнего уравнения
постановкой найденного значенияхnопределяетсяхn-1.
После решения системы уравнений методом
Гаусса необходимо делать проверку,
подставляя в исходные уравнения найденные
значения переменных хi(i= 1, …,n).
При решении системы линейных уравнений методом Гаусса все вычисления можно поместить в следующую таблицу. Рассмотрим таблицу на примере решения системы уравнений третьего порядка.
|
№ шага преобразований |
х х1 |
х х2 |
х х3 |
|
|
|
1) |
а |
а12 |
а13 |
b1 |
: |
|
0 |
а21 |
а22 |
а23 |
b2 |
|
|
|
а31 |
а32 |
а33 |
b3 |
|
|
|
1 |
|
|
|
|
|
1 2) |
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 3) |
|
|
|
|
: |
|
|
|
|
1 |
|
|
Уравнения 1), 2) и 3) составляют искомую треугольную матрицу после “прямого хода”. Число шагов преобразований в “прямом ходе” методом Гаусса равно n-1.
Коэффициенты а11,![]() ,
,![]() - называются “ведущими” элементами.
- называются “ведущими” элементами.
При “обратном
ходе” можно использовать строки таблицы,
содержащие единицы, т.е. вспомогательные
уравнения. Имеем
![]() далее
далее
![]()

![]()
![]()

![]()
ПРИМЕР:
|
№ шага |
х1 |
х2 |
х3 |
B |
|
|
|
|
4 |
1 |
2 |
12 |
: 4 |
|
|
0 |
2 |
8 |
4 |
30 |
|
|
|
|
1 |
2 |
4 |
17 |
|
|
|
|
1 |
0,25 |
0,5 |
3 |
х 2 |
х 1 |
|
1 |
0 |
7,5 |
3 |
24 |
|
|
|
|
0 |
1,75 |
3,5 |
14 |
|
|
|
|
|
1 |
0,4 |
3,2 |
х 1,75 |
|
|
2 |
|
0 |
2,8 |
8,4 |
|
|
|
3 |
|
|
1 |
3 |
|
|
Т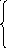 реугольная
система
реугольная
система
4 х1+х2+2х3=12
х1+х2+2х3=12
7 ,5х2+3х3=24
,5х2+3х3=24
2 ,8х3=8,4
,8х3=8,4
или
х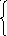 1+0,25х2+0,5х3=3
1+0,25х2+0,5х3=3
х2+0,4х3=3,2
х3=3
Обратный ход
х2=3,2-0,4∙3=2
х1=3-0,25∙2-0,5∙3=1
Вычисление определителя методом Гаусса
(третий способ, без вывода)
Определитель матицы Аравен произведению всех “ведущих” элементов при преобразовании ее по методу Гаусса.
Для вычисления определителя матрицы Авыполняется только “прямой” ход методом Гаусса, причем столбец свободных членовВстановится излишним.
ПРИМЕР: дана матрица
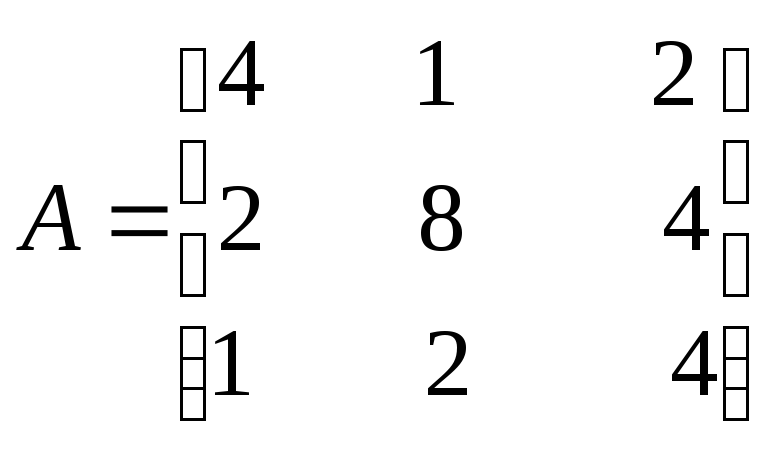 detА=4∙7,5∙2,8=84
detА=4∙7,5∙2,8=84
В ычисление
обратной матрицы методом Гаусса
ычисление
обратной матрицы методом Гаусса
А∙А-1 =Е
Матрицы АиЕизвестны, требуется определитьА-1. Обозначим столбцы матрицыА-1черезх1,х2, …,хnт.е.
![]()
Столбцы для матрицы Е обозначим через Е1,Е2, …,Еn
Тогда можем записать nсистем уравнений
А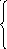 х1=Е1
х1=Е1
Ах2=Е2
Ахn=Еn
Развернем первое матричное уравнение Ах1=Е1
 х
х
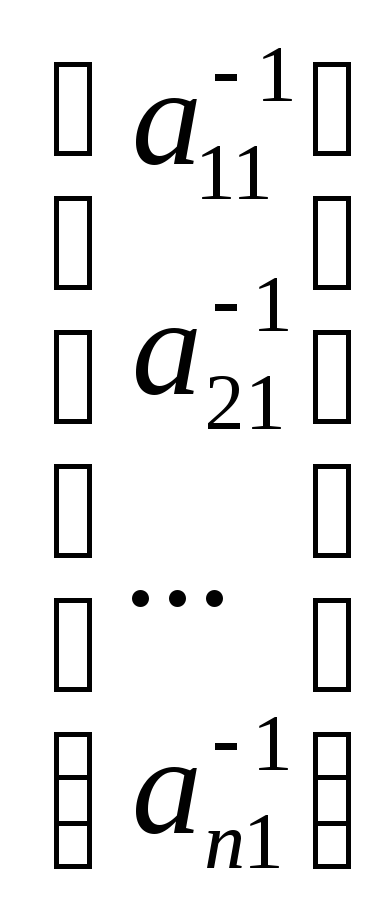 =
=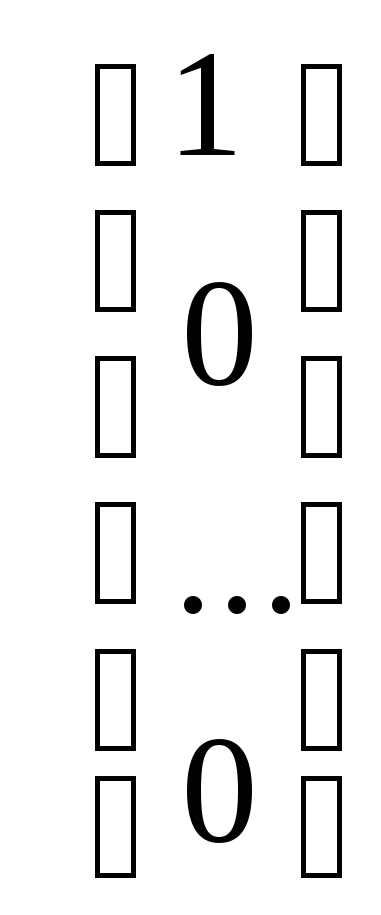
Другие матричные уравнения аналогичны.
Следовательно, для получения обратной матрицы А-1достаточно выполнитьnрешений методом Гаусса систем линейных уравнений с разными правыми частями -yстолбцами матрицыЕ.
Полученные решения х1,х2, …,хnбудут столбцами искомой обратной матрицыА-1.
Трангуляции матрицы
Квадратную матрицу Аможно представить как произведение двух треугольных матрицА=LW, где
L– нижняя треугольная матрица,
W– верхняя треугольная матрица.
Матрица Wвычисляется при прямом ходе Гаусса
а11а12а13…а1n
0
![]()
![]() …
…
![]()
0 0
![]() …
…
![]()
… … … … …
0 0 0 …
![]()
У матрицы Lнаоборот все элементы выше главной диагонали нулевые. Остальные элементы матрицыLвычисляются в результате деления элементов по столбцам, полученных при том же прямом ходе Гаусса, на ведущие элементы. Сначала вычисляются элементы первого столбца матрицыLделением на ведущий элемента11, затем после первого шага “прямым ходом” метода Гаусса вычисляются элементы второго столбца, начиная с диагонального, делением на ведущий элемента11и т.д.
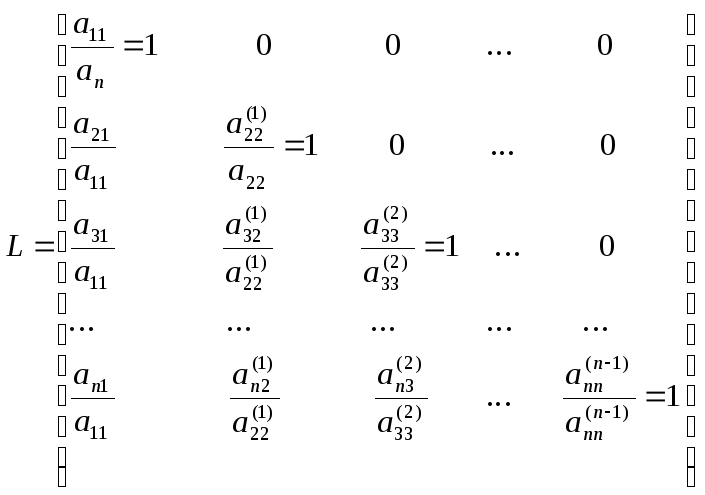
Требуется решить системы уравнений
Ах=В
Так как А=LWтоLWх=В
Обозначим Wх=Z
Тогда вместо системы Ах=Вможем записать ей эквивалентную
L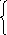 Z=В
Z=В
Wx=Z (5)
Решение эквивалентной системы с треугольными матрицами LиWзанимает гораздо меньше времени, чем решение исходной системыАх=В. Это обстоятельство очень важно при необходимости решать систему уравнений многократно при одной и той же матрицеАи разных векторах свободных членовВ, что обычно имеет место при расчетах режимов работы электрических систем. Триангуляция же матрицыАпроводится только один раз.
Т о
есть элементы матрицыА– это, как
правило, параметры схемы замещения эл.
системы,В– вектор узловых токов
или мощностей. Часто ставится задача
определения параметров большего числа
режимов при изменении токов или мощностей
потребителей в узлах при неизменной
схеме замещения. Если триангуляция
матрицыАосуществлена, то можно
быстро пользуясь системой (5) посчитать
необходимые режимы, меняя в этой системе
вектор В. Для каждого режима сначала
решается треугольная подсистемаLZ=ВотносительноZпоследовательной
подстановкой в уравнения подсистемы
найденных значений неизвестных из
предыдущих уравнений, начиная сZ1
о
есть элементы матрицыА– это, как
правило, параметры схемы замещения эл.
системы,В– вектор узловых токов
или мощностей. Часто ставится задача
определения параметров большего числа
режимов при изменении токов или мощностей
потребителей в узлах при неизменной
схеме замещения. Если триангуляция
матрицыАосуществлена, то можно
быстро пользуясь системой (5) посчитать
необходимые режимы, меняя в этой системе
вектор В. Для каждого режима сначала
решается треугольная подсистемаLZ=ВотносительноZпоследовательной
подстановкой в уравнения подсистемы
найденных значений неизвестных из
предыдущих уравнений, начиная сZ1
Z1 =b1
![]() =b2
=b2
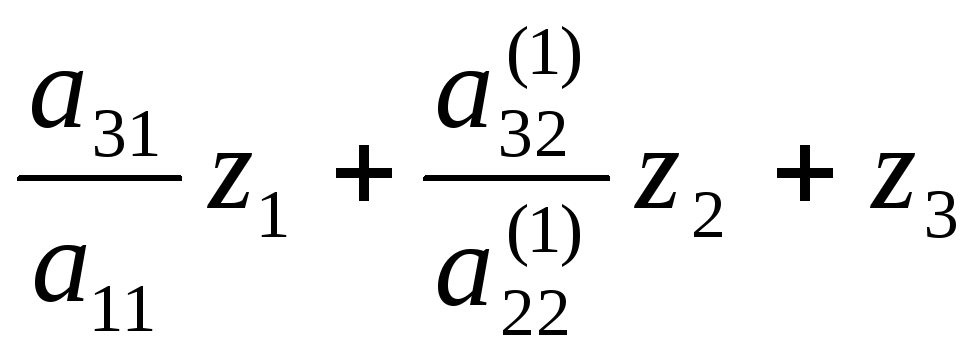 =b3
=b3
… … … … …
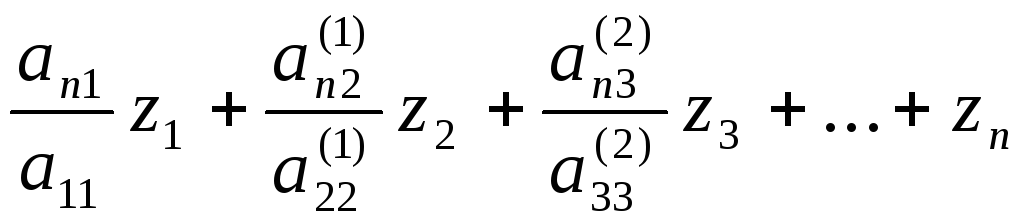 =bn
=bn
Значение Z1уже известно из первого уравнения,Z2определяется из второго уравнения подстановкой в него значенияZ1и т.д. Определяются всеZ. Затем аналогично решается вторая треугольная подсистемаWx=Zпутем обратной подстановки, начиная схn(аналогично обратному ходу методом Гаусса).
Метод Жордана-Гаусса
Метод Жордана-Гаусса называют еще методом Гаусса без обратного хода. Сущность его состоит в том, что на втором шаге переменная исключается из всех уравнений, кроме второго, на третьем шаге исключается также из всех уравнений, кроме третьего и т.д. После шагов в каждом уравнении остается одна неизвестная, т.е. получим решение системы таким образом, исключение переменных по методу Жордана-Гаусса эквивалентно преобразованию матрицы коэффициентов в единичную. Рассмотрим таблицу вычислений по методу Жордана-Гауса.
|
№ шага преобразований |
|
A |
|
C |
B |
|
0 |
а11 |
a12 |
… |
a1n |
b1 |
|
а21 |
a22 |
… |
a2n |
b2 | |
|
а31 |
a32 |
… |
a3n |
b3 | |
|
… |
… |
… |
… |
… | |
|
|
аn1 |
an2 |
… |
ann |
bn |
|
1 |
1 |
|
… |
|
|
|
0 |
|
… |
|
| |
|
0 |
|
… |
|
| |
|
… |
… |
… |
… |
… | |
|
0 |
|
… |
|
| |
|
… |
… |
… |
… |
… |
… |
|
n |
1 |
0 |
… |
0 |
|
|
0 |
1 |
… |
0 |
| |
|
.. |
.. |
… |
… |
| |
|
0 |
0 |
… |
1 |
|
Нахождение обратной матрицы методом Жордана-Гаусса
Р ассмотрим
вычислительную процедуру определителя
А-1на конкретном примере.
ассмотрим
вычислительную процедуру определителя
А-1на конкретном примере.
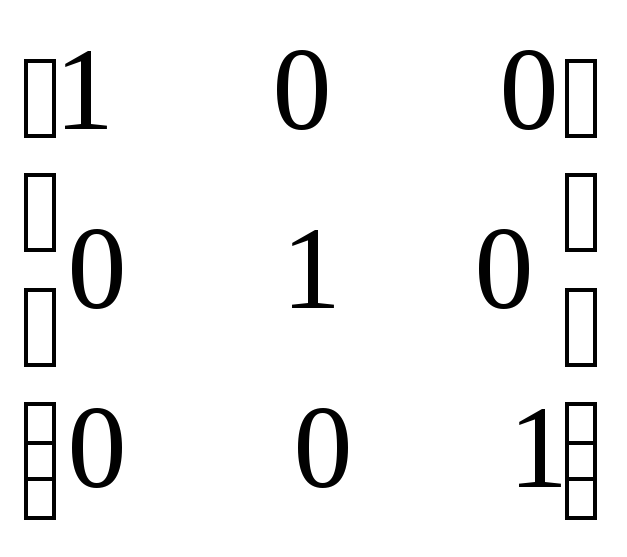
А∙А-1=Е
Пусть

Ах1х2 х3Е1Е2Е3
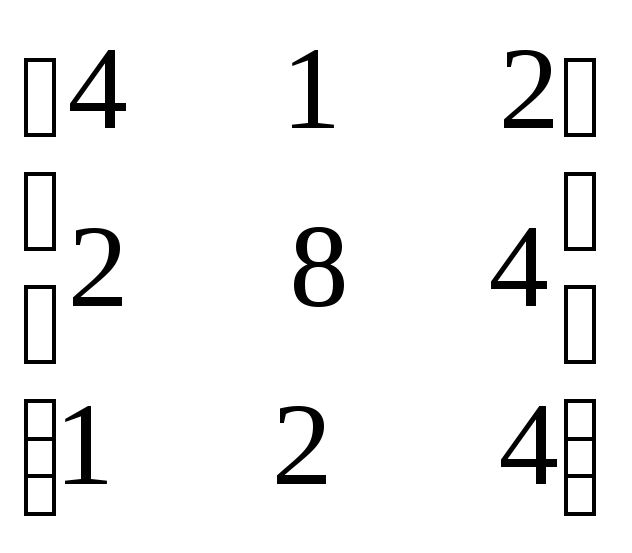 х
х
 =
=
|
№ шага преобразования |
х х1 |
х х2 |
х х3 |
Е1 |
Е2 |
Е3 |
|
|
4 |
1 |
2 |
1 |
0 |
0 |
|
0 |
2 |
8 |
4 |
0 |
1 |
0 |
|
|
1 |
2 |
4 |
0 |
0 |
1 |
|
|
1 |
0,25 |
0,5 |
0,25 |
0 |
0 |
|
1 |
0 |
7,5 |
3 |
-0,5 |
1 |
0 |
|
|
0 |
1,75 |
3,5 |
-0,25 |
0 |
1 |
|
|
1 |
0 |
0,4 |
0,2667 |
-0,0333 |
0 |
|
2 |
0 |
1 |
0,4 |
-0,0667 |
0,1333 |
0 |
|
|
0 |
0 |
2,8 |
-0,1333 |
-0,2333 |
1 |
|
|
1 |
0 |
0 |
0,2857 |
0 |
-0,1428 |
|
3 |
0 |
1 |
0 |
-0,0477 |
0,1666 |
-0,1428 |
|
|
0 |
0 |
1 |
-0,0476 |
-0,0833 |
0,357 |
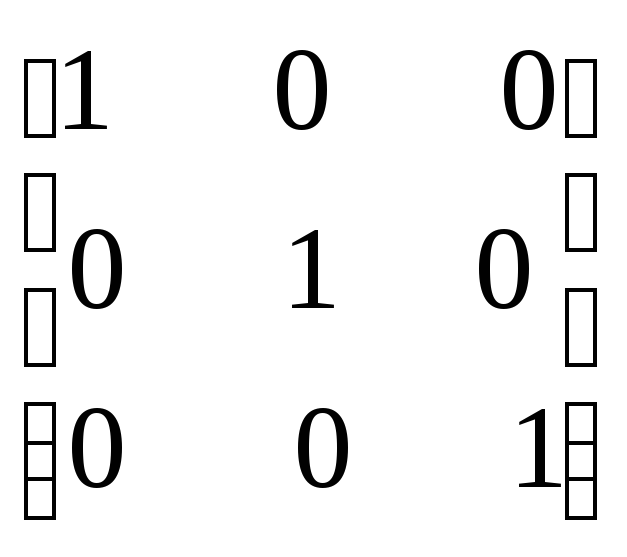
Проверка:
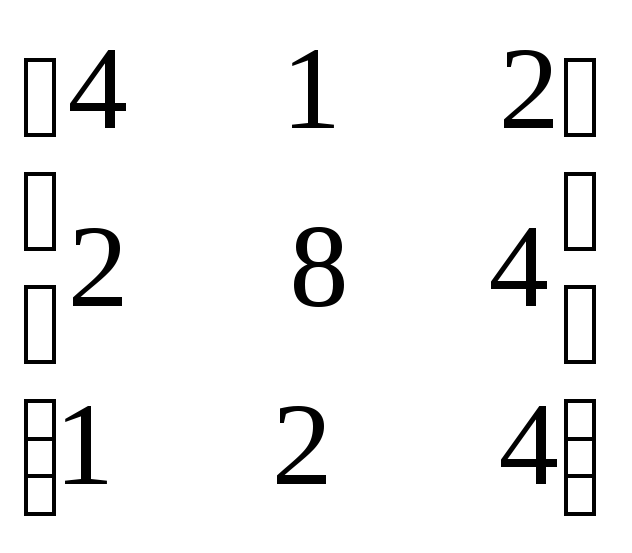 х
х
 =
=
По такой же вычислительной схеме можно вычислять значения переменных х1,х2,х3, …,хпри одной матрице коэффициентаАи разных столбцах свободных членовВ1,В2,В3, …,Вn.
Недостатки метода Гаусса (его недостатки и способы их устранения)
Если определитель матрицы Амал, то из-за ошибок округлений сильно снижается точность получения искомых корней.
Метод Гаусса требует, чтобы диагональные элементы в процессе исключения переменных не были равны нулю (т.к. строки делятся на них). Поэтому часть применяют метод Гаусса с выбором главного элемента, который заключается в следующем. При обращении в нуль элементов первого столбца из всей матрицы выбирается наибольший элемент и затем в нуль элементы второго столбца, рассматривается сокращенная матрица (путем вычеркивания в уже полученной системе первого уравнения) и в ней наибольший элемент переставляется на ее первое место и т.д.
Метод Гаусса требует большего объема памяти ЭВМ по сравнению с итерационными методами. Существуют различные приемы по сокращению занимаемой памяти ЭВМ при решении методом Гаусса электроэнергетических задач.
Например, необходимо решить систему
Yy ∙Uy=Iy
при использовании метода узловых напряжений.

Перенумерация
Экономичность памяти
Сокращение времени счета
|
Y= |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
→ |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
1 |
+ |
|
|
|
|
|
|
+ |
+ |
|
1 |
+ |
+ |
+ |
|
|
|
|
|
|
|
3 | ||
|
2 |
|
+ |
|
|
|
|
+ |
+ |
|
|
2 |
+ |
+ |
|
+ |
|
|
|
|
|
|
6 | ||
|
3 |
|
|
+ |
+ |
|
|
|
|
|
|
3 |
+ |
|
+ |
|
+ |
|
|
|
|
|
10 | ||
|
4 |
|
|
+ |
+ |
|
+ |
|
|
|
|
4 |
|
+ |
|
+ |
|
|
+ |
|
|
|
14 | ||
|
5 |
|
|
|
|
+ |
+ |
|
|
|
|
5 |
|
|
+ |
|
+ |
|
|
|
|
|
17 | ||
|
6 |
|
|
|
|
+ |
+ |
|
|
+ |
|
6 |
|
|
+ |
|
|
+ |
+ |
+ |
+ |
|
21 | ||
|
7 |
|
+ |
|
|
|
+ |
+ |
|
|
|
7 |
|
|
|
+ |
|
+ |
+ |
|
|
+ |
24 | ||
|
8 |
+ |
+ |
|
|
|
|
|
+ |
+ |
|
8 |
|
|
|
|
|
+ |
|
+ |
|
|
26 | ||
|
9 |
+ |
|
|
|
|
+ |
|
+ |
+ |
+ |
9 |
|
|
|
|
|
+ |
|
|
+ |
+ |
27 | ||
|
10 |
|
|
|
|
|
|
|
|
+ |
+ |
10 |
|
|
|
|
|
|
+ |
|
+ |
+ |
|
(30 х 70)
Я=10 х 10=100 Я=52 (26)
В ряде случаев для нахождения корней системы линейных уравнений удобнее пользоваться приближенными итерационными методами (или методами последовательных приближений).

 11
11 а11
а11