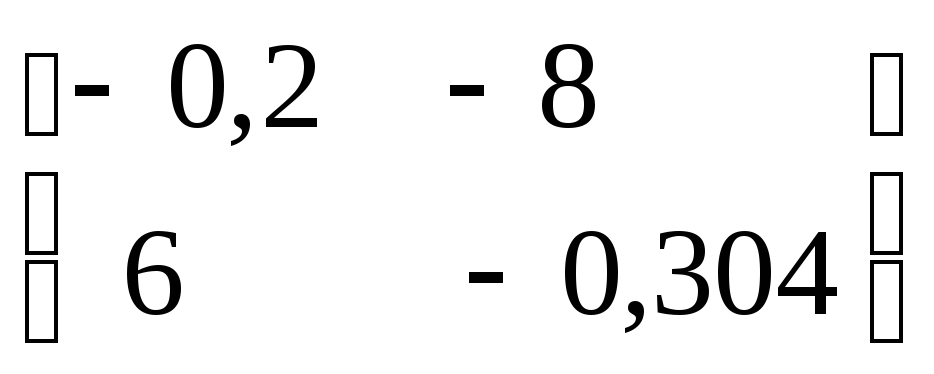- •Федеральное агентство по образованию
- •Определитель
- •Миноры и алгебраические дополнения
- •Второй способ вычисления определителя
- •Третий способ вычисления определителя
- •Действия с матрицами
- •Транспонированная матрица
- •Обратная матрица
- •Алгоритм получения обратной матрицы
- •2.2 Геометрический образ электрической сети
- •2.3. Уравнения законов Ома и Кирхгофа в матричной форме
- •2.4. “Прямой ” расчет токораспределения в электрической сети
- •2.5. Метод узловых напряжений для расчета токораспределения
- •2.6. Метод контурных токов [л-4, с.25-228]
- •Раздел 2. Методы решения систем алгебраических уравнений
- •Тема 2.I методы решения систем линейных уравнений
- •Метод обратной матрицы
- •Метод Крамера
- •Метод Гаусса
- •Метод простой итерации
- •Достаточное (но не необходимое) условие сходимости итерационного процесса
- •Метод Зейделя
- •Преимущества и недостатки итерационных методов
- •Тема 2.2 решение систем нелинейных уравнений Понятие о системах нелинейных уравнений и методах их решения
- •Решение нелинейного уравнения методом Ньютона
- •Решение системы нелинейных уравнений методом Ньютона
Решение системы нелинейных уравнений методом Ньютона
Система нелинейных уравнений решается методом Ньютона аналогично.
Пусть дана система нелинейных уравнений
f 1(х1,
. . .,хn)=0;
1(х1,
. . .,хn)=0;
f2(x1, . . .,хn)=0;
… … …;
fn(х1, . . . ,хn)=0.
Эта система заменяется системой линеаризованных уравнений
![]() ;
;
![]() ;
;
… … … … … ;
![]() .
.
В




 матричном виде система (2) записывается
матричном виде система (2) записывается
![]()
![]() …
…![]() ∆х1f1(х1,х2,
…,хn)
∆х1f1(х1,х2,
…,хn)
![]()
![]() …
…![]() х ∆х2=f2(х1,х2,
…,хn)
х ∆х2=f2(х1,х2,
…,хn)
… … … … … …
![]()
![]() …
…![]() ∆хnfn(х1,х2, …,хn)
∆хnfn(х1,х2, …,хn)
или в общем матричном виде
![]() ,
(8)
,
(8)
где
![]() - матрица Якоби; ∆х– вектор-столбец
поправок;F(х) –
вектор-столбец невязок.
- матрица Якоби; ∆х– вектор-столбец
поправок;F(х) –
вектор-столбец невязок.
Данная система линейных уравнений может быть решена любым известным численным методом (например, методом Гаусса).
Алгоритм решения системы нелинейных уравнений методом Ньютона состоит из следующих действий:
Зададим начальные приближения
 ,
, ,
…,
,
…, .
.Вычислим невязки f1(х1,х2, …,хn),f2(х1,х2, …,хn), …,fn(х1,х2, …,хn).
Вычислим все элементы матрицы частных производных
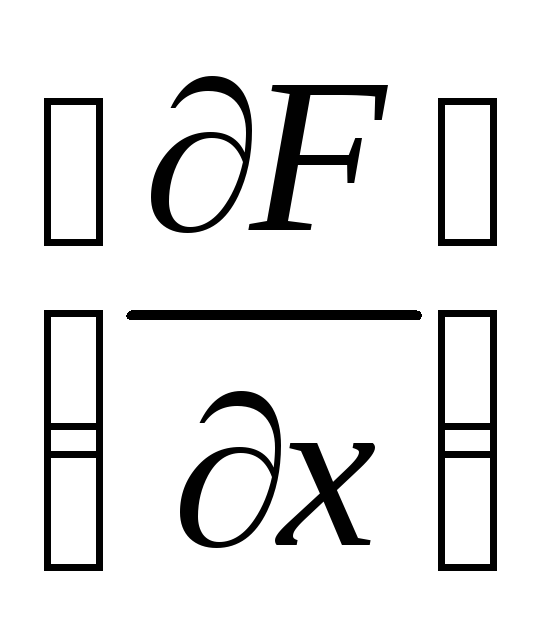 прих1=
прих1= ,х2=
,х2=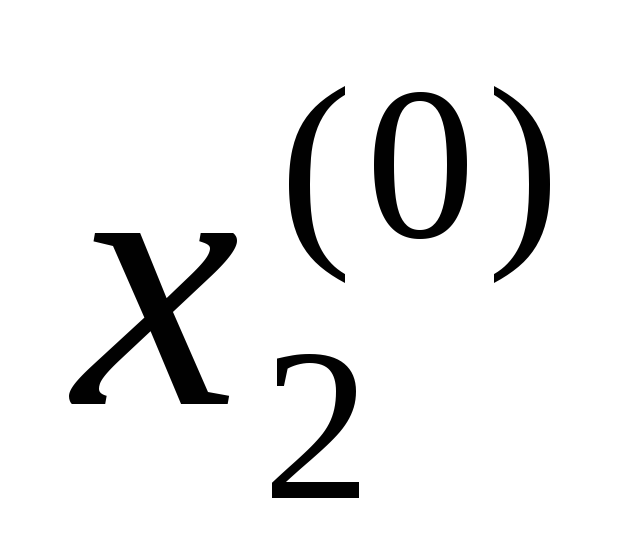 ,
…,хn=
,
…,хn=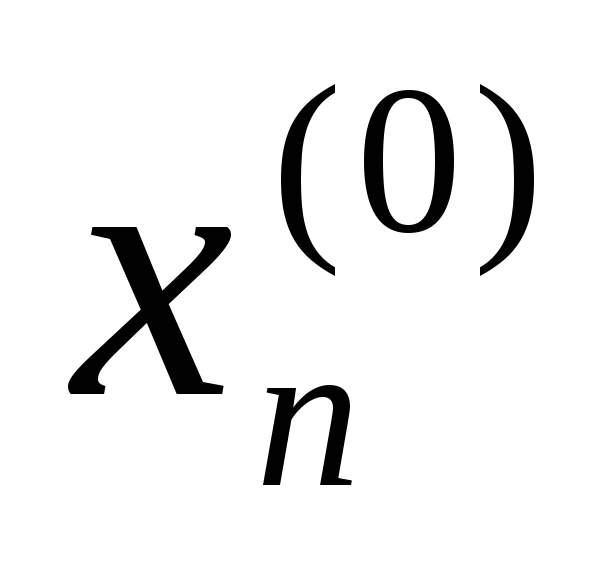 .
.Найдем поправки
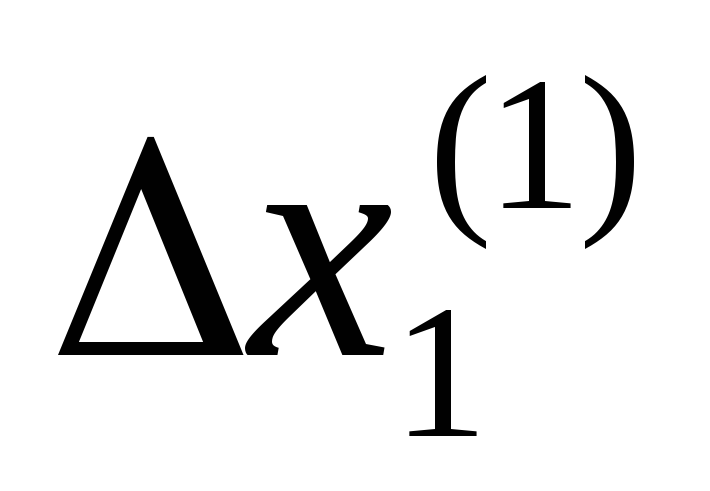 ,
, ,
…,
,
…,
Для этого решим систему линейных уравнений
![]()
численным методом относительно поправок ∆х(1).
Определим новые приближения
![]()
![]()
Вычислим невязки f1(х1,…,хn),f2(х1,…,хn), …,fn(х1,…,хn)
Проверим условия
|f1(х1,…,хn)|≤ε1;
|fn(х1,…,хn) )|≤εn.
Если не выполняется
хотя бы одно из nусловий, то производим
следующую итерацию – повторяем действия
3-7, уже используя полученные значения![]() ,
,![]() ,
…,
,
…,![]() .
Итерационный процесс нахождения корней
системы нелинейных уравнений будем
продолжать до выполнения всех условий
без исключения.
.
Итерационный процесс нахождения корней
системы нелинейных уравнений будем
продолжать до выполнения всех условий
без исключения.
Метод Ньютона эффективен в том случае, когда известны хорошие начальные приближения неизвестных, достаточно близкие к корням системы нелинейных уравнений. Это условие в наших задачах, как правило, удается выполнить.
Пример: нужно решить систему нелинейных уравнений
![]()
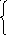 (при ε=0,01)
(при ε=0,01)
![]()
0 итерация1.![]() ;
2.
;
2.![]() ;
;![]()
1 итерация
1.
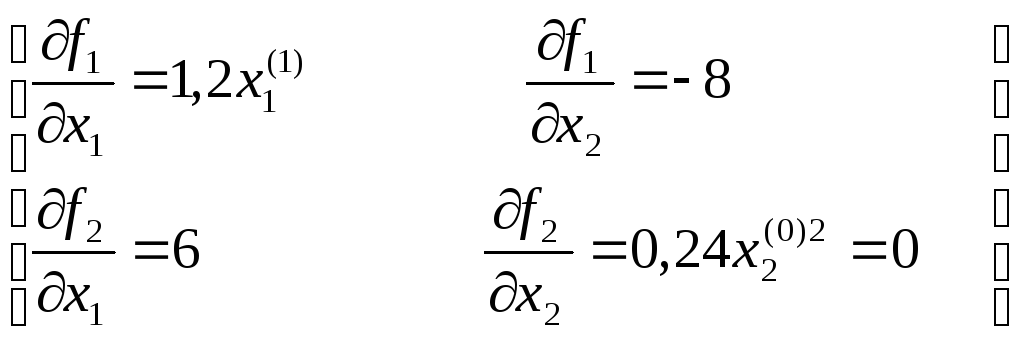
2.
![]() х
х![]() =
=![]() или
или ;
;
Отсюда
![]() ;
;![]() .
.
3.
![]() ;
;
![]() .
.
4.
![]() ;
|0,01667|>ε
;
|0,01667|>ε
![]() ;
|0,114|>ε
;
|0,114|>ε
2 итерация
1.

2.
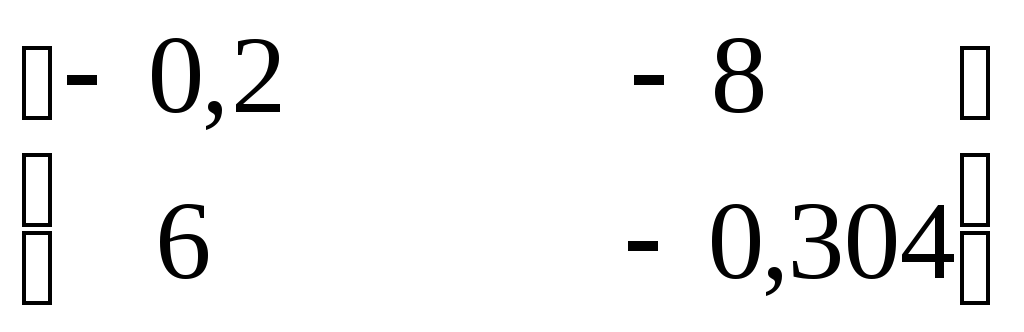 х
х![]() =
= ;
;
3.
![]() ;
;
![]() ;
;
4.
![]() 0,0002714<ε
0,0002714<ε
![]() 0,0000071<ε
0,0000071<ε
Результаты расчетов сведем в таблицу
|
№ итерации |
|
∆х |
хк |
f(к) | |||
|
|
|
|
|
|
| ||
|
0 |
- |
- |
|
0 |
0 |
9 |
1 |
|
1 |
|
0,1667 |
-1,125 |
-0,1667 |
1,125 |
0,01667 |
0,114 |
|
2 |
|
-0,0191 |
-0,0016 |
-0,1476 |
1,1266 |
0,0002714 |
0,0000071 |