А); б) ; в) .

Вычисление предела, где, всегда начинают с подстановки впредельного значения её аргумента. Если в результате получают неопределённостьили, то для её раскрытия применяют правило Лопиталя: ,где и- функции, дифференцируемые в окрестности. В некоторых случаях может потребоваться неоднократное применение данного правила. На каждом этапе его применения следует использовать, упрощающие отношение, тождественные преобразования, а также комбинировать это правило с любыми другими известными приёмами вычисления пределов. Раскрытие неопределённостей вида: ,,,,путём преобразований:,,сводят к раскрытию неопределенностей видаили.

Решение.

а) ,где

,

Тогда .

б) ,где

,

.

Тогда . Применяем правило Лопиталя ещё раз:, где

,

=.

Тогда .

в) . Преобразуем данную неопределённость (приведением разности дробей к общему знаменателю) к виду, после чего применим правило Лопиталя. Получим

=,где

,

.

Тогда .

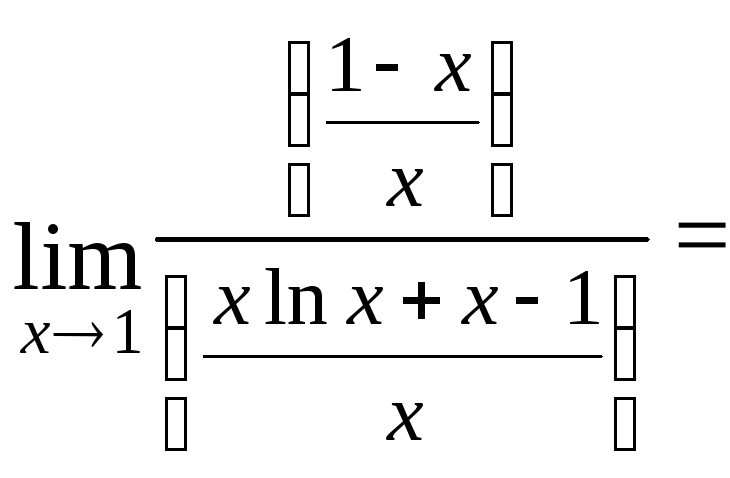
Применяем правило Лопиталя ещё раз:

, где ,

.

В итоге получим .

Ответ:

а); б);в).

51-60. Для указанной функции требуется:

а) провести полное исследование функции и построить её график; б) найти наибольшее и наименьшее значения функции на отрезке ;

в) составить уравнение касательной к графику функции в точке .

а) ; б),; в),.

Для построения графика функции нужно:

1) найти область определения функции;

2) найти область непрерывности функции и точки разрыва;

3) исследовать функцию на чётность, нечётность и периодичность;

4) найти точки пересечения графика с осями координат;

5) найти асимптоты графика функции;

6) найти интервалы возрастания и убывания, экстремумы функции;

7) найти интервалы выпуклости, вогнутости и точки перегиба.

Решение.

а1) Находим область определения функции: =).

а2) Поскольку данная функция является элементарной, то областью её непрерывности является область определения , а точками разрыва являются точкии, не принадлежащие множеству, но являющиеся предельными точками этого множества (точками в любой окрестности которых содержатся точки данного множества). Исследуем характер разрыва в точкахи, вычислив в них односторонние пределы функции:

, ,

, .

Так как односторонние пределы функции в точках и- бесконечные, то данные точки являются точками бесконечного разрыва.

а3) Функция не является периодической.

Функция , в аналитическое выражение которой входит хотя бы одна непериодическая функция периодической не является.

Проверяем является ли функция чётной или нечётной. Так как область определения функции =) не симметрична относительно точки , то данная функция – общего вида.

а4) Находим точки пересечения графика с осями координат.

Так как , то точек пересечения графика с осьюнет.

Положим и решим уравнение. Его решением является. Следовательно, точка- точка пересечения графика с осью.

а5) Находим вертикальные и наклонные асимптоты графика функции.

Прямая является вертикальной асимптотой, тогда и только тогда, когдаявляется точкой бесконечного разрыва функции.

Так как точки и- точки бесконечного разрыва данной функции, то вертикальными асимптотами графика функции являются прямыеи.

Прямая является наклонной асимптотой графика функциипритогда и только тогда, когда одновременно существуют конечные пределы:и.

Вычисляем сначала пределы при : ,.

В дальнейшем будем иметь в виду следующий часто встречающийся предел:

Следовательно , т.е.- наклонная (горизонтальная) асимптота графика функции при.

Аналогично вычисляем пределы при : ,Следовательно , т.е.- наклонная (горизонтальная) асимптота графика функции при.

а6) Определяем интервалы возрастания, убывания, экстремумы функции. Для этого находим первую производную функции:

и определяем критические точки функции , т.е. точкив которыхилине существует:

;

не существует при и.

Таким образом, единственной критической (стационарной) точкой функции является точка.

Исследуем знак производной в интервалах, на которые критические точки функцииразбивают её область определения, и найдём интервалы возрастания, убывания, экстремумы функции. Результаты исследования представим следующей таблицей:

	+	+
	возрастает	возрастает		убывает	убывает

Так как при переходе слева направо через точкупроизводнаяменяет знак с «+» на «», то точкаявляется точкой локального максимума и.

а7) Определяем интервалы выпуклости, вогнутости, точки перегиба графика функции. Для этого находим вторую производную функции:

и определяем точки возможного перегиба , т.е. точкив которыхилине существует:, так как(квадратное уравнение не имеет действительных корней);не существует прии.

Таким образом, функция не имеет точек возможного перегиба.

Исследуем знак второй производной в интервалах, на которые точки возможного перегиба функцииразбивают её область определения, и найдём интервалы выпуклости, вогнутости, точки перегиба графика функции. Результаты исследования представим следующей таблицей:

	+		+
	график вогнутый	график выпуклый	график вогнутый

Точек перегиба нет.

а8)На основании полученных результатов строим график функции (рис.3)

Рис.3.

Наибольшее и наименьшее значения функции непрерывной и кусочно-дифференцируемой (дифференцируемой, за исключением, быть может, конечного числа точек) на отрезкедостигается или в точках, в которыхилине существует, или на концах отрезка.

б1) Находим первую производную функции:

и определяем внутренние критические точки функции , т.е. точкив которыхилине существует:

, точек в которыхне существует нет. Таким образом, единственной внутренней критической (стационарной) точкой функциина отрезкеявляется точка.

б2) Вычисляем значения функции во внутренних критических точках и на концах отрезка:,,.

б3) Сравниваем значения ,,и находим наименьшее и наибольшее значения функциина отрезке:

, .

Уравнение касательной к графику функции в точкеимеет вид:

в1) Вычисляем значение функции в точке:

.

в2) Находим первую производную функции:

и вычисляем её значение в точке :.

в3) Составляем уравнение касательной: и записываем его в виде :.

Ответ: а) Рис.3; б) ,;в) .

61 – 70. Для указанной функции требуется: а) найти дифференциал и вторую частную производную ;б) вычислить приближённо (с помощью первого дифференциала) значение функции в точке, если,,.

Первый дифференциал функции имеет вид.

Частные производные функции вычисляются по обычным правилам дифференцирования функции одной переменной, в предположении, что если производная берётся по аргументу(аргументу), то другой аргумент(аргумент) считается постоянным.

Решение.

а1) Находим частные производные первого порядка ифункции

:

;

.

Тогда первый дифференциал функции имеет вид:

.

а2) Вторую частную производную (или кратко) находим как первую частную производную по аргументуот функции :

.

Формула для приближённого вычисления значений функции в малой окрестности точки, в которой функция дифференцируема, имеет вид:, где,. Формула тем точнее, чем меньше значение.

б) Вычисляем значения частных производных ,и значение функциив точке, где,:

, ,.

Тогда, учитывая, что ,, получим:

.

Ответ: а),; б).

71 – 80. Найти локальные экстремумы функции .

Для нахождения локальных экстремумов дифференцируемой функции необходимо: 1) Найти область определения функции.2) Найти первые частные производные ифункции.3) Решить систему уравнений (необходимое условие экстремума) и найти точки(с учётом возможных дополнительных ограничений на значения аргументови) возможного локального экстремума функции.4) Найти вторые частные производные ,,; составить выражениеи вычислить значенияив каждой точкевозможного экстремума.5) Сделать вывод о наличии экстремумов функции , используя достаточное условие экстремума: если , то в точкеэкстремума нет; еслии, то в точке- локальный минимум; еслии, то в точке- локальный максимум; если, то требуется дополнительное исследование точки(например, по определению).6) Найти локальные экстремумы (экстремальные значения) функции.

Решение.

1) Находим область определения функции

2) Находим первые частные производные и:

;

.

3) Составим систему уравнений и решим её. Получим четыре решения:,,,. Из них точками возможного экстремума функции в области являются только две точки:и.

4) Находим вторые частные производные:

;

;

,

составляем выражение и вычисляем:

; ,.

5) Делаем вывод о наличии экстремумов. Так как:

, то в точке экстремума нет;

,, то в точке- локальный минимум.

6) Находим локальный минимум

.

Ответ: .

81–90. а) Найти условные экстремумы функции при условии .

Для нахождения методом Лагранжа локальных экстремумов дифференцируемой функции при условиинеобходимо:1) Найти область определения функции.2) Составить функцию Лагранжа , где- неопределённый постоянный множитель Лагранжа.3) Решить систему уравнений (необходимое условие условного экстремума) и найти точкивозможного условного локального экстремума и соответствующие им значениямножителя Лагранжа.4) Найти выражение второго дифференциала функции Лагранжа в точкахпри условии, чтоисвязаны уравнением.5) Сделать вывод о наличии экстремумов функции при условии , используя достаточное условие условного экстремума. Если для всех,(одновременно), связанных уравнением,, то в точке- локальный максимум; если, то в точке- локальный минимум. Еслипринимает как положительные, так и отрицательные значения, то в точкеэкстремума нет.6) Найти локальные условные экстремумы функции .

Решение.

1) Находим область определения функции .

2) Составляем функцию Лагранжа: .

3) Записываем необходимое условие условного экстремума ,

где: ,

. Получим . Решая систему, находим две точки возможного условного экстремума функции в области и соответствующие им значения множителя Лагранжа:приипри.

4) Находим выражение второго дифференциала функции Лагранжа

.

Вычисляем при условии, учитывая, что:

;

.

Получим:

;

.

5) Делаем вывод о наличии экстремумов. Так как для всех :, то в точке- условный локальный минимум;

, то в точке - условный локальный максимум.

6) Находим условные минимум и максимум функции при условии:

,

Ответ: , при условии.

81–90. б) Найти наибольшее и наименьшее значения функции:

в области: ,,.

Функция , дифференцируемая в ограниченной замкнутой области, достигает своего наибольшего и наименьшего значений или в стационарных точках, или в точках границыобласти. Для их нахождения необходимо:1) Найти все стационарные точки функции и вычислить в них значения функции.2) Найти наибольшее и наименьшеезначения функции на границе, задаваемой одним аналитическим выражением в явном видеили. Если, гдезадаются одним аналитическим выражением в явном виде, то находят наибольшие и наименьшие значенияифункции на каждом из участковграницы.3) Сравнить значения функции ,,и выбрать из них наибольшееи наименьшеезначения функции в области.

Решение. Изображаем область (она представляет собой треугольник, ограниченный прямыми,,), находим стационарные точкифункции, решая систему уравнений

, и вычисляем в них значения функции .

Учитывая, что: ,, получим. Отсюда,и, следовательно, единственной стационарной точкой функции в областиявляется точка.

Вычислив значение функции в этой точке, получим .

2) Границу областипредставляем в виде, где:,;:,;:,и находим наибольшие и наименьшие значения функции на каждом из участков границы:,,,,,.

На участке :,:. Таким образом, пришли к задаче нахождения наибольшего и наименьшего значений функции одной переменнойна отрезке. Эти значения функция принимает или в критических точках, принадлежащих интервалуили на концах отрезка. Для их отыскания находим первую производную функции: и определяем её внутренние критические точки, т.е. точкив которыхилине существует:, точекв которыхне существует нет. Вычисляем значения функцииво внутренних критических точках (таких точек нет) и на концах отрезка:,. Сравнивая значения,находим наименьшее и наибольшее значения функциина отрезке:,.

На участке:,:. Таким образом, пришли к задаче нахождения наибольшего и наименьшего значений функции одной переменнойна отрезке. Эти значения функция принимает или в критических точках, принадлежащих интервалуили на концах отрезка. Для их отыскания находим первую производную функции: и определяем её внутренние критические точки, т.е. точкив которыхилине существует:, точекв которыхне существует нет. Вычисляем значения функцииво внутренних критических точках и на концах отрезка:,,. Сравнивая значения,,находим наименьшее и наибольшее значения функциина отрезке:,.

На участке :,:. Таким образом, пришли к задаче нахождения наибольшего и наименьшего значений функции одной переменнойна отрезке. Эти значения функция принимает или в критических точках, принадлежащих интервалуили на концах отрезка. Для их отыскания находим первую производную функции: и определяем её внутренние критические точки, т.е. точкив которыхилине существует:, точекв которыхне существует нет. Вычисляем значения функцииво внутренних критических точках и на концах отрезка:,,. Сравнивая значения,,находим наименьшее и наибольшее значения функциина отрезке:,

3) Сравнивая значения функции ,,,,,, , делаем вывод, что,.

Ответ: ,.

91-100. Даны комплексные числа , и алгебраическое уравнение . Требуется: а) вычислить, ,,; б)найти все корни алгебраического уравнения на множестве комплексных чисел.

Решение.

1а) Вычисляем : .

2а) Вычисляем .

Сначала находим . Тогда

.

3а) Вычисляем .

Сначала находим (учитываем, что). Тогда

4а) Вычисляем :

(учитываем, что ).

1б) Для нахождения корней алгебраического уравнения , раскладываем его левую часть на множители:

.

2б) Находим корни уравнения на множестве комплексных чисел, приравнивая каждый из множителей нулю (число корней, с учётом кратности, должно равняться порядку уравнения):

1) .

2) .

3) . Так как дискриминант квадратного уравнения, то уравнение имеет два комплексно-сопряжённых корня:.

Корни ,можно найти и как корни уравнения, по формуле. Для нахождения комплексных значений корня, числоследует представить в виде комплексного числа в тригонометрической форме:, после чего значения корня найти по формуле:,где

Ответ:

a) , , , ;

б) ,,.

101 – 110. Найти: а) производнуюфункциив точкепо направлению вектора;б) градиент функции и его величину || в точке, если:

, , .

Производная функциипо направлению векторанаходится по формуле, где,,,.

Градиент функциинаходится по формуле.

Решение.

а1) Находим первые частные производные функции :

;

;

.

а2) Вычисляем значения частных производных в точке :

,,

а3) Вычисляем направляющие косинусы вектора :

, ,,.

а4) Вычисляем значение в точке:

.

б1) Находим значение градиента функции в точке:

.

б2) Вычисляем в точке:

.

Ответ: а) ;б) ,.

111–120. Затраты, необходимые для производства единиц данной продукции задаётся функцией издержек . Продукция реализуется по фиксированной цене (ден.ед.) за единицу продукции. Требуется найти:а) оптимальное значение выпуска продукции, при котором производитель получит максимальную прибыль;б) средние значения издержек производства и прибыли при ;в) эластичность издержек производства и прибыли при . Сделать выводы.

Прибыль, получаемая производителем при выпуске единиц данной продукции, задаётся функцией, где- выручка от реализацииединиц данной продукции по фиксированной цене(ден.ед.) за единицу продукции, -функция издержек.

Средними издержками называют величину (издержки в расчёте на 1 ед. выпускаемой продукции), а средней прибылью – величину(прибыль в расчёте на 1 ед. выпускаемой продукции).

Эластичностью издержек называют величину (показывает приближённый процентный прирост издержекпри изменениина 1%), а эластичностью прибыли –(показывает приближённый процентный прирост прибылипри изменениина 1%).

Решение.

а1) Находим функцию прибыли

.

а2) Находим оптимальное значение выпуска продукции, при котором производитель получит максимальную прибыль, т.е. находим при каком значениивыпуска продукции функция прибылипримет наибольшее значение на промежутке.

Если функция одной переменной на промежуткеимеет единственную точку локального экстремума, являющуюся точкой локального максимума, то в точкефункция принимает своё наибольшее значение на промежутке.

Для решения данной задачи находим производную функции :

и определяем её критические точки (точки возможного локального экстремума), принадлежащие промежутку , т.е. точки в которыхилине существует:, точекв которыхне существует нет. Таким образом, единственной критической точкой функциина промежуткеявляется точка.

Так как приипри, то точка- является точкой локального максимума и, следовательно, точкой в которой функцияна промежуткепринимает наибольшее значение.

Итак, оптимальное значение объёма выпускаемой продукции составляет 5 единиц, при этом максимальная прибыль составляет 50 ден.ед.

б) Находим средние издержки производства и прибыль при :

;

.

Итак, в расчёте на единицу выпускаемой продукции издержки производства составляют 90 ден.ед., а прибыль – 10 ден.ед.

в) Находим эластичность издержек производства и прибыли при :

.

.

Итак, при увеличении объёма выпуска продукции на 1%, издержки производства увеличатся на 1.11%, а прибыль не изменится.

Ответ: а),;б),;

в),.