
- •Федеральное агентство по образованию
- •2. Содержание и структура дисциплины (часть 1).
- •Тема 7. Основные теоремы о дифференцируемых функциях и их приложения.
- •Тема 8. Исследование функций с помощью производных, построение их графиков.
- •Раздел III. Функции нескольких переменных.
- •Тема 9. Основные понятия о функции нескольких переменных.
- •Тема 10. Производные и дифференциалы функции нескольких переменных, их приложения.
- •Тема 11. Векторный анализ и элементы теории поля.
- •Дополнительная литература:
- •4. Методические указания по изучению дисциплины.
- •5. Материалы для контроля знаний студентов.
- •91. ,,.
- •Раздел II.Дифференциальное исчисление функции одной переменной.
- •Раздел III. Функции нескольких переменных.
- •6. Приложения.
- •6.1. Образец решения контрольных задач типового варианта.
- •Часть 1.
- •А); б) ; в) .
- •6.2. Краткие теоретические сведения.
- •Тема 1. Множества. Числовые множества. Функция.
- •Тема 2. Комплексные числа и многочлены.
- •Тема 3. Предел функции. Эквивалентные функции.
- •Тема 4. Числовые последовательности. Предел последовательности.
- •Тема 5. Непрерывность функции.
- •Тема 6. Производные и дифференциалы функции одной переменной.
- •Тема 7. Основные теоремы о дифференцируемых функциях и их приложения.
- •Тема 8. Исследование функций с помощью производных, построение их графиков.
- •7.1 Возрастание, убывание функций. Экстремум.
- •7.2 Наибольшее и наименьшее значения функции.
- •7. 3 Выпуклость, вогнутость, точки перегиба. Асимптоты.
- •7.4 Построение графиков функций.
- •Тема 9. Основные понятия о функции нескольких переменных.
- •Тема 10. Производные и дифференциалы функции нескольких переменных, их приложения.
- •Тема 11. Векторный анализ и элементы теории поля.
- •Тема 12. Неявные и выпуклые функции.
- •Тема 13. Экстремумы функций нескольких переменных.
- •Тема 14. Приложения к общей экономической теории.
- •6.3 Основные математические формулы.
- •С о д е р ж а н и е
6. Приложения.
6.1. Образец решения контрольных задач типового варианта.
Часть 1.
1-10. Требуется:
а)
найти
естественную
область определения функции
![]() ;
;
б)
установить
чётность (нечётность) функции
![]() .
.
Решение.
а) Естественную
область определения находим как множество
![]() всех значений аргумента
всех значений аргумента![]() функции, для которых формула
функции, для которых формула![]() имеет смысл:
имеет смысл:![]() .
Решив (на числовой прямой) систему
неравенств
.
Решив (на числовой прямой) систему
неравенств![]() ,
устанавливаем, что геометрическим
образом множества
,
устанавливаем, что геометрическим
образом множества![]() является промежуток
является промежуток![]() .
.
б)
Находим
сначала
естественную
область
определения функции
![]() :
:![]() .
Решив (на числовой прямой) неравенство
.
Решив (на числовой прямой) неравенство
![]() ,
устанавливаем, что геометрическим
образом множества
,
устанавливаем, что геометрическим
образом множества![]() является объединение промежутков
является объединение промежутков![]() .
.
Так
как область
![]() является симметричной относительно
точки
является симметричной относительно
точки![]() ,
то проверяем выполнение для всех
,
то проверяем выполнение для всех![]() условий:
условий:![]() или
или![]() ,
учитывая чётность и нечётность основных
элементарных функций, входящих в
аналитическое выражение
,
учитывая чётность и нечётность основных
элементарных функций, входящих в
аналитическое выражение![]() .
.
Если
область
![]() не симметрична относительно точки
не симметрична относительно точки![]() ,
то
,
то![]() на этом множестве является функцией
общего вида.
на этом множестве является функцией
общего вида.
Для
этого находим
![]() .
Поскольку
.
Поскольку![]() для всех
для всех![]()
![]()
![]() ,
то функция
,
то функция
![]() является
чётной.
является
чётной.
Ответ:
а)
![]()
![]() ,
,![]() ;
;
б)
функция
![]() - чётная.
- чётная.
11-21. Вычислить пределы (не пользуясь правилом Лопиталя):
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)![]() д)
д)![]()
Вычисление
предела
![]() ,
где
,
где![]() ,
начинают всегда с подстановки в
,
начинают всегда с подстановки в![]() предельного значения её аргумента
предельного значения её аргумента![]() .
В результате могут получиться
неопределённости
.
В результате могут получиться
неопределённости![]() ,
,![]() ,
,![]() ,
которые раскрывают тождественными
преобразованиями
,
которые раскрывают тождественными
преобразованиями![]() такими, чтобы преобразованное выражение
получилось определённым. При вычислении
пределов используют свойства конечных
пределов и бесконечно больших функций,
а также следующие известные пределы:
такими, чтобы преобразованное выражение
получилось определённым. При вычислении
пределов используют свойства конечных
пределов и бесконечно больших функций,
а также следующие известные пределы:![]()
![]() ,
,![]() ,
,
![]() (
(![]() ),
),![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Решение.
а)
![]() При подстановке
вместо переменной
При подстановке
вместо переменной
![]() её предельного значения
её предельного значения![]() получим неопределённость
получим неопределённость![]() .
Для её раскрытия сначала разделим
числитель и знаменатель дроби на
.
Для её раскрытия сначала разделим
числитель и знаменатель дроби на![]() (старшую степень переменной
(старшую степень переменной![]() в числителе и знаменателе), после чего
используем свойства конечных пределов
и бесконечно больших функций. Получим
в числителе и знаменателе), после чего
используем свойства конечных пределов
и бесконечно больших функций. Получим
![]()
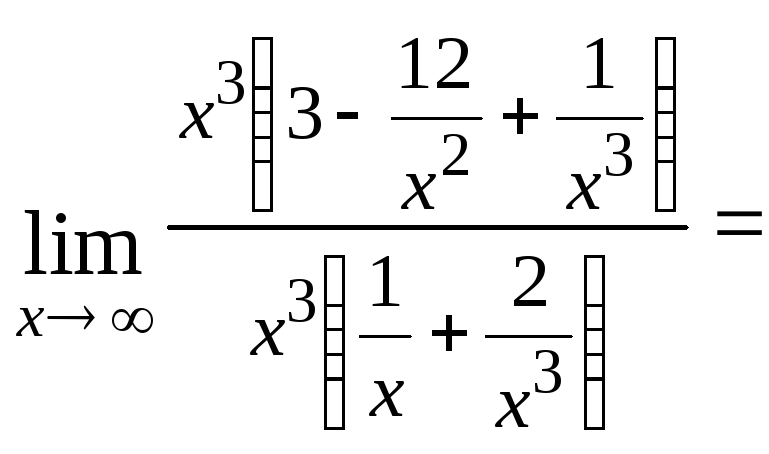

![]() .
.
б)
![]() При подстановке вместо переменной
При подстановке вместо переменной
![]() её предельного значения
её предельного значения![]() получим неопределённость
получим неопределённость![]() .
Для её раскрытия выделим в числителе и
знаменателе дроби общий множитель вида
.
Для её раскрытия выделим в числителе и
знаменателе дроби общий множитель вида![]() ,
где
,
где![]() - некоторое число, т.е. множитель
- некоторое число, т.е. множитель![]() .
Затем сократим на него числитель и
знаменатель дроби, после чего используем
свойства пределов.
.
Затем сократим на него числитель и
знаменатель дроби, после чего используем
свойства пределов.
1)
В
квадратном трёхчлене
![]() множитель выделяют разложением
квадратного трёхчлена по формуле
множитель выделяют разложением
квадратного трёхчлена по формуле![]() ,
где
,
где![]() .2)
В выражении
.2)
В выражении
![]() множитель выделяют следующим способом:
множитель выделяют следующим способом:![]()
![]()
![]() .
.
В
результате получим
![]()

![]()
![]()
![]() .
.
в)
![]() При подстановке вместо переменной
При подстановке вместо переменной
![]() её предельного значения
её предельного значения![]() получим неопределённость
получим неопределённость![]() .
Выделим в числителе множители вида
.
Выделим в числителе множители вида![]() ,
где
,
где![]() при
при![]() и используем свойства пределов. Получим
и используем свойства пределов. Получим
![]()

![]()
Для
раскрытия неопределённостей
![]() ,
содержащих тригонометрические и обратные
тригонометрические функции, в числителе
и знаменателе дроби выделяют сначала
множители вида:
,
содержащих тригонометрические и обратные
тригонометрические функции, в числителе
и знаменателе дроби выделяют сначала
множители вида:![]() ,
,![]() ,
,![]() ,
,![]() ,
где
,
где![]() при
при![]() ,
используя формулы тригонометрии:
,
используя формулы тригонометрии:
![]() ,
,
![]() ,
,
![]() .
После чего
применяют свойства пределов, учитывая,
что:
.
После чего
применяют свойства пределов, учитывая,
что:
![]() ,
,![]() ,
,![]() ,
,![]() .
.


 .
.
г)
![]() При подстановке вместо переменной
При подстановке вместо переменной
![]() её предельного значения
её предельного значения![]() получим неопределённость
получим неопределённость![]() .
.
Для
раскрытия неопределённости
![]() ,
возникающей при вычислении предела
,
возникающей при вычислении предела![]() ,
где
,
где![]() ,
,![]() ,
сначала выражение
,
сначала выражение
![]() представляют в виде
представляют в виде![]() ,
где
,
где![]() при
при![]() .
После чего используют свойства пределов,
заменяя выражение
.
После чего используют свойства пределов,
заменяя выражение![]() его предельным значением
его предельным значением![]() и учитывая, что
и учитывая, что![]() =
= .
.
Представим
![]() в виде
в виде![]() ,
где
,
где![]() при
при
![]() ,следующим
способом:
,следующим
способом:
![]()
![]() =
= .
Тогда учитывая, что
.
Тогда учитывая, что ,
,![]()
 ,
получим
,
получим
![]() =
=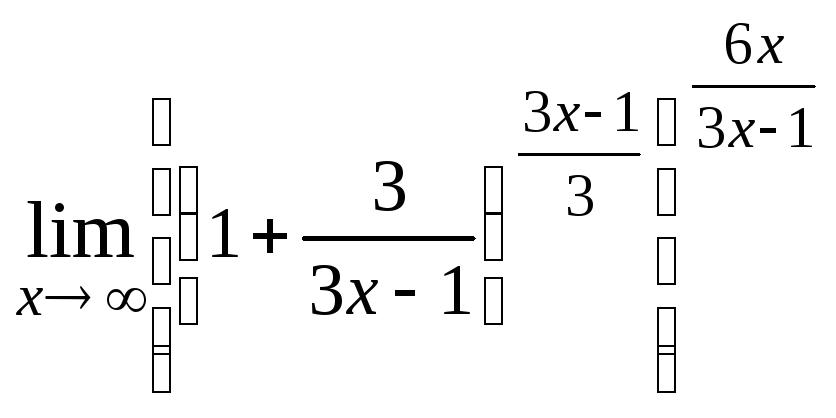
![]() =
=![]() .
.
д)
![]()
Для
вычисления предела
![]() ,
где
,
где![]() представляет собой дробь, числитель и
знаменатель которой содержат факториалы
натурального числа
представляет собой дробь, числитель и
знаменатель которой содержат факториалы
натурального числа![]() ,
поступают следующим образом. Выделяют
в числителе и знаменателе в качестве
общего множителя факториал меньшего
натурального числа и сокращают на него.
В результате получают выражение, предел
которого находят рассмотренными выше
способами.
,
поступают следующим образом. Выделяют
в числителе и знаменателе в качестве
общего множителя факториал меньшего
натурального числа и сокращают на него.
В результате получают выражение, предел
которого находят рассмотренными выше
способами.
Для
вычисления данного предела сначала
выразим
![]() ,
,![]() ,
,![]() через
через![]() :
:![]() ,
,![]() ,
,![]() ,
после чего сократим числитель и
знаменатель на
,
после чего сократим числитель и
знаменатель на![]() :
:
![]()
![]()
![]()
![]() .
.
В
результате получили неопределённость
![]() .
Для её раскрытия разделим числитель и
знаменатель дроби
.
Для её раскрытия разделим числитель и
знаменатель дроби![]() на
на
![]() (старшую степень переменной
(старшую степень переменной![]() числителя и знаменателя), после чего
используем свойства пределов. Получим
числителя и знаменателя), после чего
используем свойства пределов. Получим
![]()


![]() .
.
Ответ:
а)![]() ;
б)
;
б)![]() ;в)
;в)![]() ;
г)
;
г)![]() ;
д)
;
д)![]() .
.
21-30.
Для
указанной функции
![]() требуется:
а) выяснить
при каких значениях параметра
требуется:
а) выяснить
при каких значениях параметра
![]() функция
будет
непрерывной;
б) найти
точки разрыва
функции и исследовать их характер.
Построить
график функции.
функция
будет
непрерывной;
б) найти
точки разрыва
функции и исследовать их характер.
Построить
график функции.
а)
![]() ;
б)
;
б) .
.
Решение.
Точками
разрыва функции
 являются точки разрыва функций
являются точки разрыва функций![]() в промежутках
в промежутках![]() ,
,![]() ,…,
,…,![]() ,
кроме того, точками возможного разрыва
функции
,
кроме того, точками возможного разрыва
функции![]() являются точки
являются точки![]() в окрестности которых и в самих точках
функция задаётся разными аналитическими
выражениями.
в окрестности которых и в самих точках
функция задаётся разными аналитическими
выражениями.
Точка
![]() является точкой непрерывности функции
является точкой непрерывности функции![]() тогда и только тогда, когда:
тогда и только тогда, когда:![]() .
.
а)
Поскольку
функции
![]() и
и![]() непрерывны в промежутках
непрерывны в промежутках![]() и
и![]() как элементарные функции, определённые
в каждой точке данных промежутков, то
непрерывность
функции
как элементарные функции, определённые
в каждой точке данных промежутков, то
непрерывность
функции
![]() может
нарушиться только в точке её возможного
разрыва
может
нарушиться только в точке её возможного
разрыва
![]() .
.
Определяем
значение параметра
![]() из условия непрерывности функции
из условия непрерывности функции![]() в точке
в точке![]() :
:
![]() .Вычисляя
.Вычисляя
![]() ,
,![]() ,
,![]() :
:![]() ,
,![]() ,
,![]() ,
из условия непрерывности
,
из условия непрерывности![]() ,
находим
,
находим![]() .
.
График
непрерывной функции
![]() имеет вид изображённый на рис. 1.
имеет вид изображённый на рис. 1.
б)
Функции
![]() и
и![]() непрерывны в промежутках
непрерывны в промежутках![]() и
и![]() как элементарные функции, определённые
в каждой точке данных промежутков, а
функция
как элементарные функции, определённые
в каждой точке данных промежутков, а
функция![]() в промежутке
в промежутке![]() имеет точкой разрыва точку
имеет точкой разрыва точку![]() ,
в которой она не определена. Тогда для
функции
,
в которой она не определена. Тогда для
функции
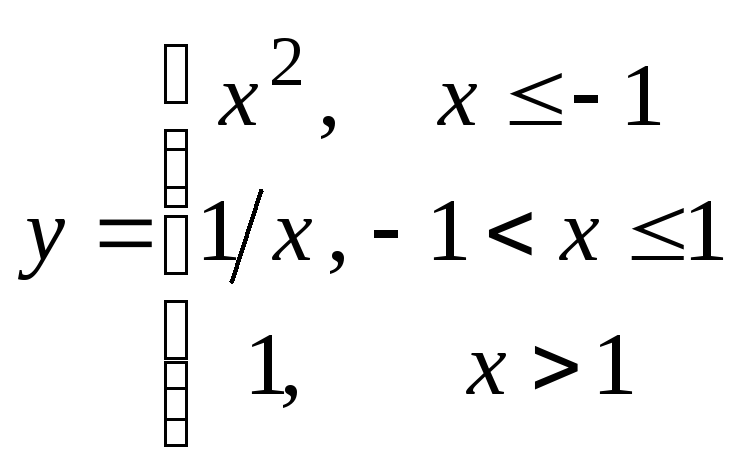 точка
точка
![]() является точкой разрыва, а точки
является точкой разрыва, а точки![]() и
и![]() ,
в окрестности которых и в самих точках
функция задаётся разными аналитическими
выражениями, являются точками возможного
разрыва.
,
в окрестности которых и в самих точках
функция задаётся разными аналитическими
выражениями, являются точками возможного
разрыва.
Исследуем
на непрерывность точки
![]() :
:
1)
![]()
![]()
![]()
![]()
![]() .
.
Следовательно,
точка
![]() - точка разрыва 1-го рода функции
- точка разрыва 1-го рода функции![]() .
.
2)
![]()
![]() Следовательно,
точка
Следовательно,
точка
![]() - точка бесконечного разрыва (2-го рода)
функции
- точка бесконечного разрыва (2-го рода)
функции![]() .
.
3)
![]()
![]()
![]()
![]()
![]() .
.
Следовательно,
точка
![]() - точка непрерывности функции
- точка непрерывности функции![]() .
.
График
функции
 имеет вид, изображённый на рис.2.
имеет вид, изображённый на рис.2.
Ответ:
а) Функция
![]() непрерывна при
непрерывна при![]() (рис.1);б)
(рис.1);б)
![]() - точка разрыва 1-го рода,
- точка разрыва 1-го рода,
![]() -точка
бесконечного разрыва функции
-точка
бесконечного разрыва функции
![]() (рис.2).
(рис.2).![]()


Рис.1 Рис.2
31-40.
Найти
производную
![]() :
:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Нахождение
производной
![]() функции
функции![]() заданной явно, с помощью правил
дифференцирования:
заданной явно, с помощью правил
дифференцирования:
![]() (
(![]() ),
),![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() сводят к нахождению табличных производных.
сводят к нахождению табличных производных.
Производную
![]() функции
функции![]() заданной параметрическими уравнениями
заданной параметрическими уравнениями![]() находят в параметрическом виде по
формуле
находят в параметрическом виде по
формуле![]() .
.
Решение.
а)
![]() ,
где
,
где
![]()
![]() =
=![]() ;
;
![]()
![]()
![]()
![]()
Тогда
 .
.
б)
 ,где
,где
![]()
![]()

![]()
![]() .
.
![]()
![]()
![]()
![]() .
.
Тогда
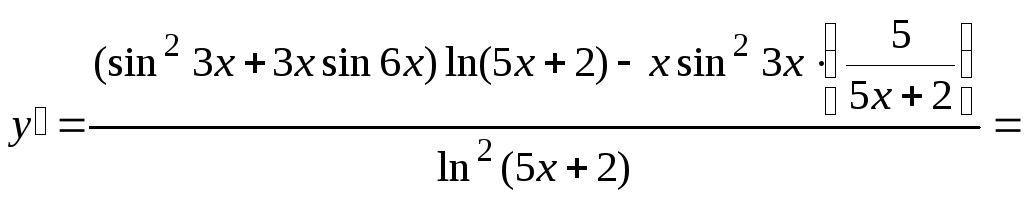
![]() .
.
в)
Производную
функции
![]() ,
заданной параметрическими уравнениями
,
заданной параметрическими уравнениями
![]() находим по
формуле
находим по
формуле
![]() ,где
,где
![]()
![]()
![]()
![]() ;
;
![]()
![]()
![]() .
.
Тогда
 .
.
41-50. Вычислить пределы, используя правило Лопиталя.
