3. Примеры линейных многошаговых схем

Для случая K=2 с учетом (48), (50) имеем

vⁿ⁺²=₁vⁿ⁺¹+₀vⁿ, q²–₁q–₀=0.

Отсюда

, ,

где

, .

Рис. 1.13. Линейные многошаговые схемы в плоскости неопределённых коэффициентов ( K = 2 )

Условия |q₁(, a₀,b₀)|≤1, |q₂(,a₀,b₀)|≤1 ограничивают областьA-устойчивых схем. На рис. 1.13 эта область в плоскости свободных коэффициентов {a₀,b₀} заштрихована (четырехугольникA₁,A₂,A₃,A₄). Сплошная прямаяB₁B₂— множество схем третьего порядка аппроксимации — не пересекается с множествомA-устойчивых схем. ТочкаB₂на этой прямой — единственная в этом случае схема четвертого порядка аппроксимации (49). И в общем случае доказано (теорема Далквиста), чтолинейныхмногошаговыхA-устойчивыхсхемспорядкомаппроксимациивышевторогонесуществует.

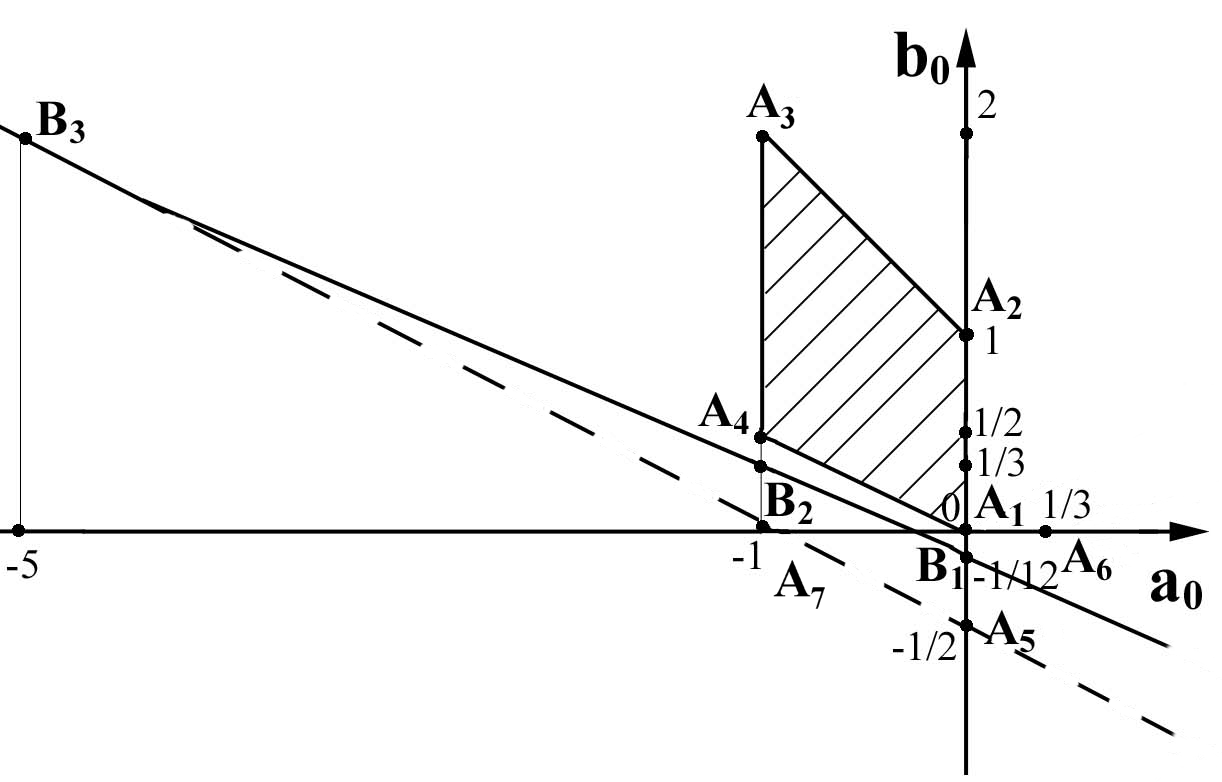
Точка A_с координатами

a₀=1/3, b₀=0 (53)

— единственная в этом случае L-устойчивая схема (схема Кёртисса–Хиршфельдера). Область жестко-устойчивых схем, очевидно, содержится внутри себя множествоA-устойчивых схем. В частности, схема, соответствующая точкеA₆, является жестко-устойчивой.

Точка A₁с коэффициентами

a₀=b₀=0, (54)

т. е. одношаговая линейная схема (метод трапеций), из числа A-устойчивых схем является оптимальной в том смысле, что она среди другихA-устойчивых схем приK=2 ближе всего расположена и кL-устойчивой схеме (точкеA₆), и к схемам 3–го порядка (наиболее точная изA-устойчивых схем).

Отметим еще схему 3-го порядка точности, соответствующую точке B₁. Она является жестко-устойчивой и наиболее близка к множествуA-устойчивых схем. Для этой схемы

a₀=0, b₀= –1/12. (55)

Явным схемам на рис. 1.13 соответствует штриховая прямая. В частности, точкаA₅с коэффициентами

a₀ = 0, b₀ = –1/2 (56)

— явная схема Адамса. Все явные схемы, как видно, не являются A-устойчивыми. А в целом, семейство линейных многошаговых схем существенно беднее схем типа Рунге–Кутты.

5. Схемы для продолженных систем (схемы Обрешкова)

   1. Алгоритм и аппроксимация

Лучшие черты методов Рунге–Кутты и линейных многошаговых методов сочетают схемы для продолженной системы (19) или линейные многошаговые схемы с использованием 2-й (схемы Обрешкова) и более высоких производных:

v_tt(t, v) = f_t = f/t + f_v f. (57)

Добавляя в (43) линейную комбинацию вторых производных v_tt с дополнительными неопределенными коэффициентамис_k, получим для этих схем (a_K= 1)

,

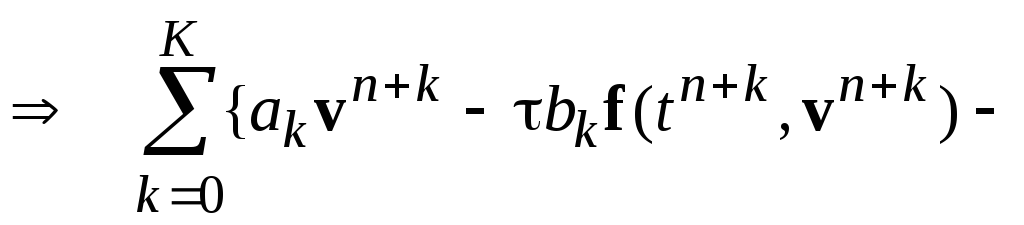(58)

.

Из начальных условий в (18) и из (57) видно, что v_tt(0, v⁰) фактически можно считать известным.

Условия аппроксимации, как и в случае линейных многошаговых методов, являются линейными (относительно неопределенных коэффициентов a_k, b_k, c_k) уравнениями:

, (59)

(обеспечивают 1-й порядок аппроксимации),

(60)

(обеспечивает 2-й порядок аппроксимации вместе с (59)),

…

(61)

(обеспечивает -й порядок аппроксимации на решениях (18) вместе с предшествующими условиями).

В случае неявных схем (b_K  0,c_K  0) нелинейная относительноv^n+kсистема (58) с ограничениями (59) – (61):

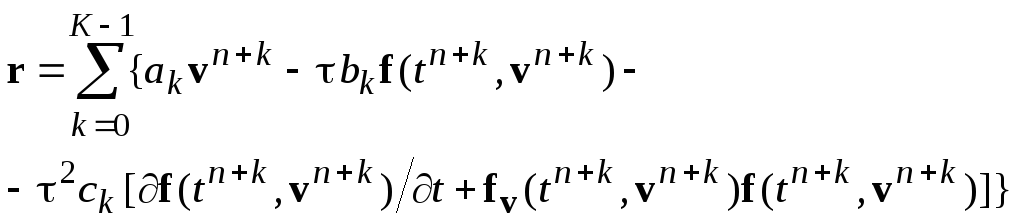
решается каким-либо итерационным методом, например,

s = 0,1, …, , (62)

B = R/v^n+k = E – b_kf_v – ²c_k[(f/t)/v + f_vf_v + C].

В (62) С— матрица, столбцами которой являются векторы

((f_v)/v₁)f, ((f_v)/v₂)f, …, ((f_v)/v_K)f. (63)