МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Московский физико-технический институт

(государственный университет)

А.С. Холодов, А.И. Лобанов, А.В. Евдокимов

РАЗНОСТНЫЕ СХЕМЫ ДЛЯ РЕШЕНИЯ ЖЕСТКИХ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ПРОСТРАНСТВЕ НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ

Методические указания к лабораторным работам

по курсу «Нелинейные вычислительные процессы»

Москва  2001

Содержание

1. Численное интегрирование жестких систем обыкновенных дифференциальных уравнений (ОДУ) 4

2. Примеры жёстких систем ОДУ 42

Список литературы 49

1. Численное интегрирование жестких системобыкновенных дифференциальных уравнений (оду)

   1. Жесткие оду

      1. Линейные однородные уравнения 1-го порядка

Рассмотрим вначале простейшее уравнение:

(1)

на отрезке

(2)

и задачу Коши для (1):

u(0)= u₀. (3)

Решение (1) – (3), очевидно,

. (4)

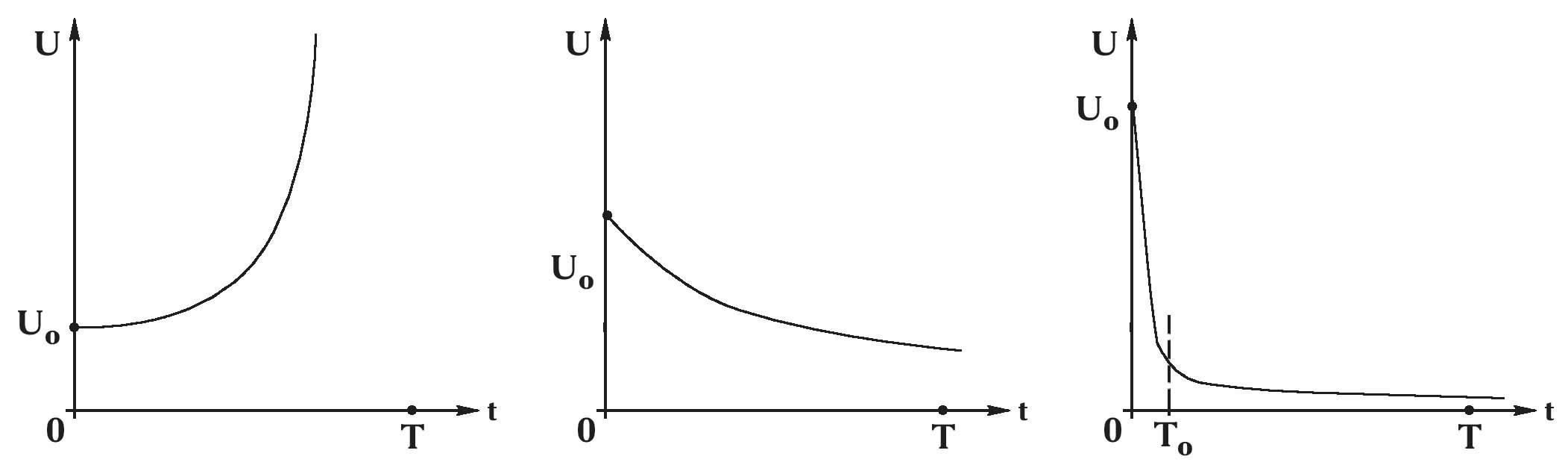
Если , имеем неограниченное (неустойчивое) решение (рис. 1.1). В этом случае надо просто интегрировать (1) с шагом по времени, обеспечивающим необходимую точность, до тех пор, пока это возможно.

Рис. 1.1.	Рис. 1.2.	Рис. 1.3.

Если , то решение задачи (1) – (3) ограниченное (). С точки зрения вычислителя здесь важна величина отрезка интегрированияT. Если, то имеем обычную ситуацию (рис. 1.2), можно пользоваться стандартными методами численного интегрирования (Эйлера, Эйлера–Коши, Рунге–Кутты, Адамса и т. д.). Если, то имеем решение типа «пограничного слоя» (рис. 1.3) с резким изменениемuна малом (в масштабеT) отрезке [0, T₀]. Если положение «пограничного слоя» заранее неизвестно, при численном интегрировании возникают осложнения, которые будут рассмотрены ниже. Основная идея заключается в том, чтобы численный метод обеспечивал качественно правильное поведение численного решения на участке «пограничного слоя» (при), т. е. быстрое затухание, и возможно точнее воспроизводил решение на основном участке интегрирования(вне «пограничного слоя»).

2. Системы линейных однородных уравнений

Пусть на отрезке (2) рассматривается Jуравнений (1):

j= 1, …,J(5)

с начальными условиями . Если обозначить

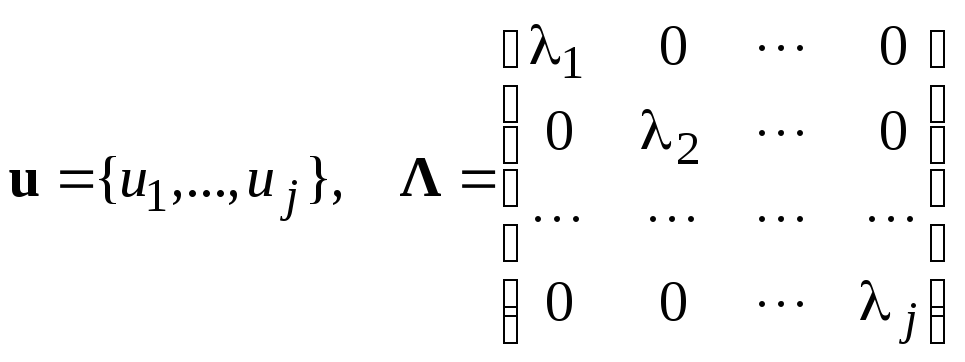
и перейти к векторной форме

, (6)

то, сделав замену , где

,

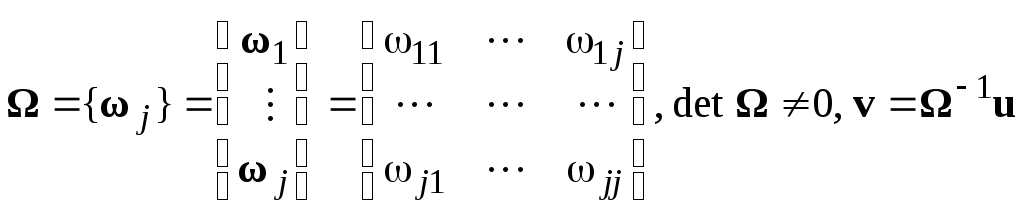получим вместо (6) однородную линейную систему ОДУ:

. (7)

Так как , то.

Наоборот, если задана система (7), то умножая ее скалярно Jраз на левые собственные векторыматрицыA, определяемые, как это следует из (7), с точностью до их длины, изJлинейных однородных систем

или (8)

приходим к эквивалентной (7) совокупности уравнений (5), связанных друг с другом только через начальные условия

v(0) =v₀или. (9)

Здесь — собственные значения матрицыA, т. е. корни характеристического уравнения

, (10)

где — многочлен степениJ.

Решение каждого из уравнений (5) имеет вид (4), т. е. , а значит, решение задачи Коши (7), (9) есть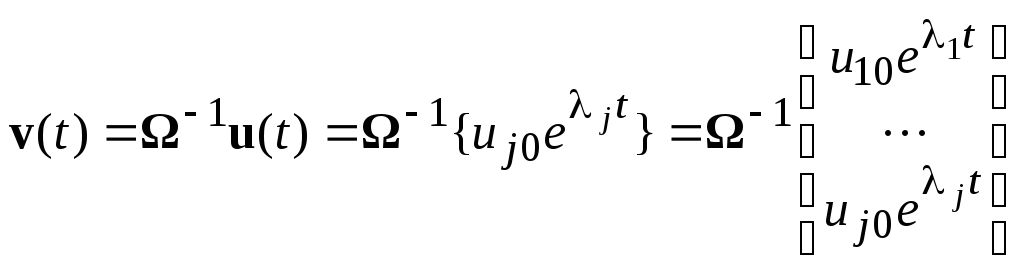, т. е. является линейной комбинацией экспонент (если вседействительны) или имеет более сложный характер с присутствием гармонических составляющих (если средибудут комплексно-сопряженные корни уравнения (10)).

3. Пример: задача Коши для линейного однородного уравнения второго порядка

, , 

(,a,b— константы).

Обозначим и введем вектор, тогда

,

или, в векторной форме,

, ,

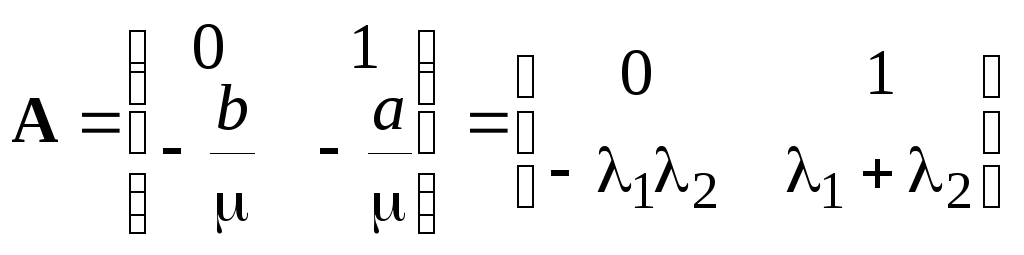где — собственные значения матрицыAиз (10):

,

.

При |a|~|b|~1,приближенно имеем,;,. Далее, из (8):

, ,

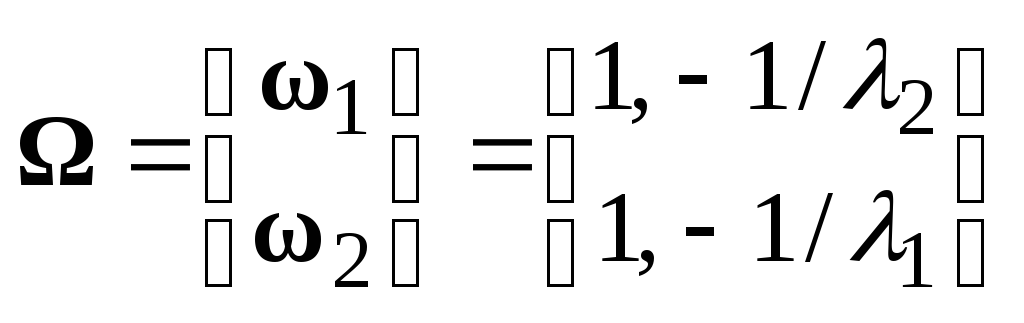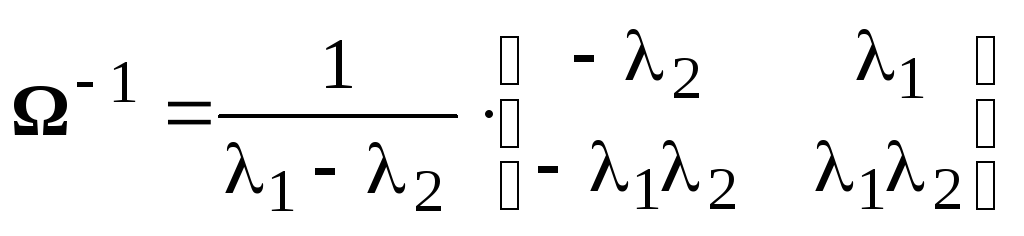при .

Тогда, учитывая , получаем

,

.

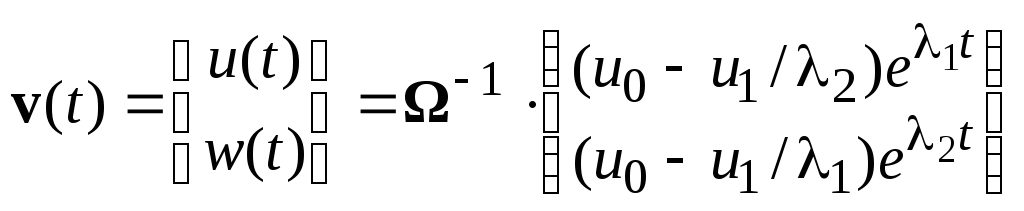Если оба действительны, то имеем комбинацию двух экспонент, затухающих при λ₁ < 0 и λ₂ < 0. Если λ₁ = α + iβ, λ₂ = α – iβ, тоu(t) = e^αt{[(u₁– αu₀) sin(βt)]/β ++ u₀ cos(βt)}, и на экспонентуe^αtнакладываются гармонические колебания с периодомT^*~1/β, т. е. характер поведения решения определяется собственными значениями матрицыA.

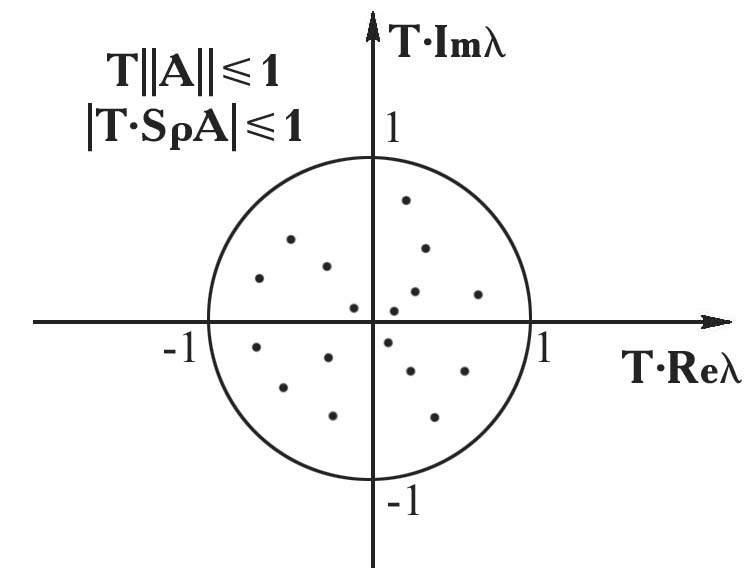
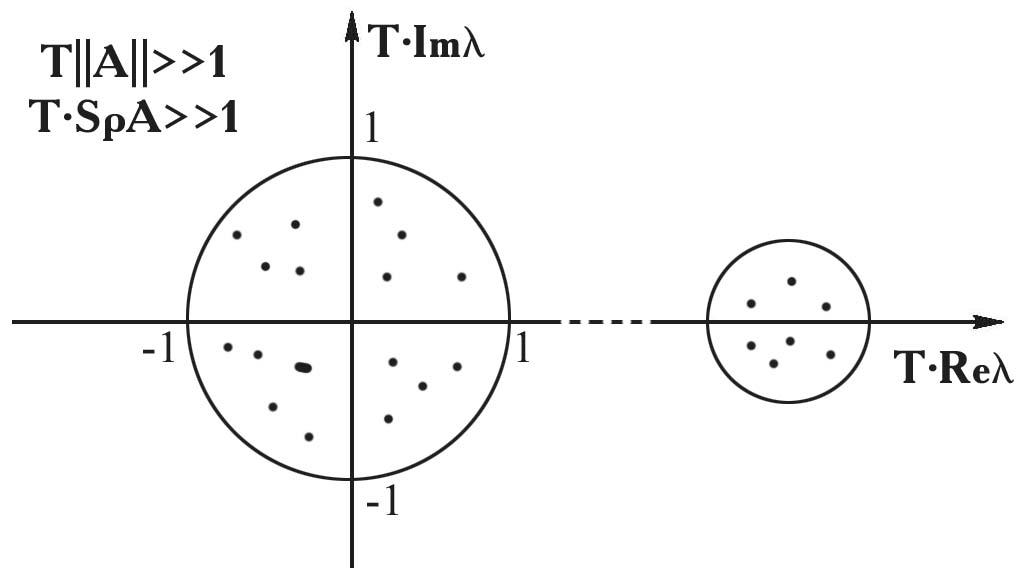
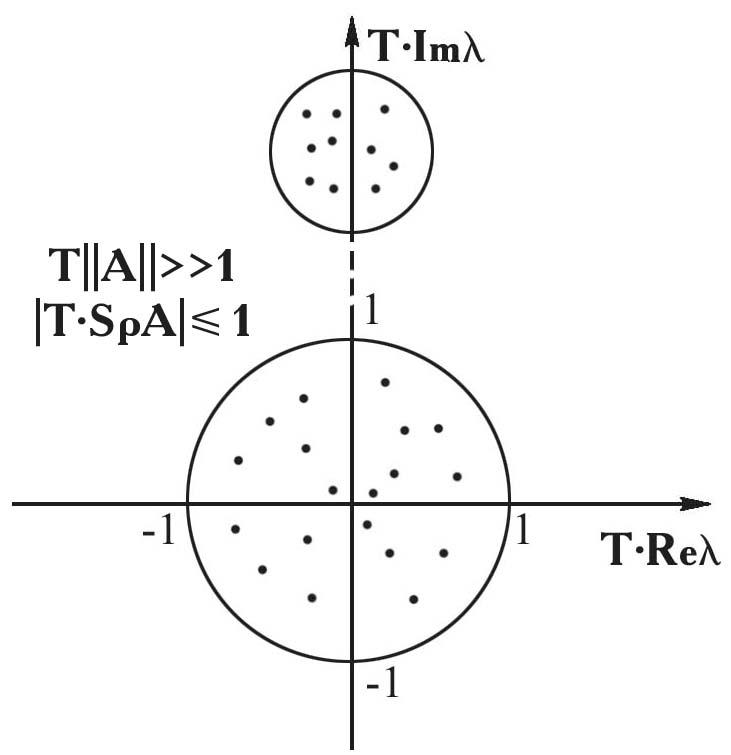
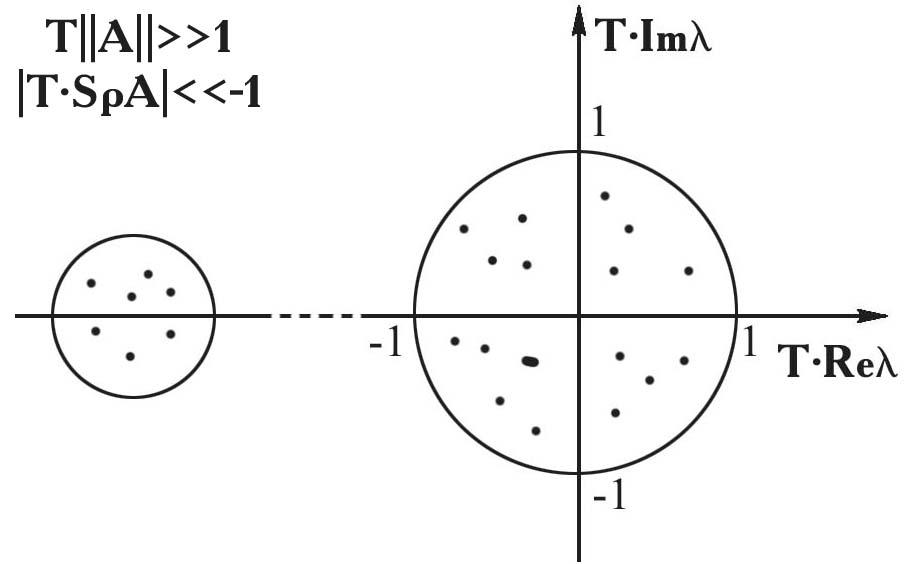
В общем случае можно выделить четыре ситуации:

а	б
в	г
Рис. 1.4. Виды спектров матриц систем ОДУ

Здесь —следА, ||A|| — её норма.

Случай ане сложен для расчётов; проходят стандартные схемы (явные схемы Рунге–Кутты, Адамса т. п.).

Случай бпрактически безнадежен (неустойчивые по Ляпунову системы ОДУ).

Случай вдовольно часто встречается на практике, и для него есть специальные методы, основанные на осреднении быстро осциллирующих гармоник.

Случай гмы и будем рассматривать (жесткие системы ОДУ). Для матрицыAбольшой размерности найти все собственные числа(полная спектральная задача) не очень просто из-за ее плохой обусловленности. Действительно, для жесткой системы число обусловленности матрицыA

(11)

или, приближенно, ||A||Т >> 1.