3. Одношаговые методы типа Рунге–Кутты

   1. Алгоритм

Перейдем к общему случаю системы (18). Одношаговые методы типа Рунге–Кутты имеют вид:

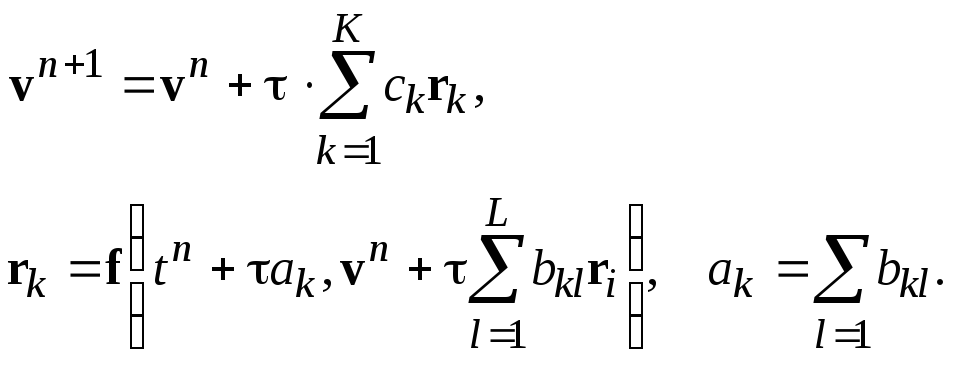(21)

В дальнейшем для описания конкретных вариантов метода будем пользоваться таблицей Бутчера:

a1	b11	b12	…	b1K
a2	b21	b22	…	b2K
…	…	…	…	…
ak	bK1	bK2	…	bKK
	c1	c2	…	cK

Для явных схемРунге–КуттыL < k, и таблица Бутчера выглядит следующим образом:

a1	0	0	…	0	0
a2	b21	0	…	0	0
a3	b31	b32	…	0	0
…	…	…	…	…	…
ak	bK1	bK2	…	bKK–1	0
	c1	c2	…	cK–1	cK

В этом случае для расчёта vⁿ⁺¹поvⁿв соответствии с (21) имеем простые рекуррентные соотношения:

— предиктор,

(22)

— первый корректор и т. д.

«Полуявные» или «диагонально неявные» схемыРунге–Кутты отличаются от явных наличием ненулевых элементов на главной диагонали таблицы Бутчера (L≤k):

a1	b11	0	…	0
a2	b21	b22	…	0
…	…	…	…	…
ak	bK1	bK2	…	bKK
	c1	c2	…	cK

В этом случае на каждом шаге по времени последовательно решаются нелинейные системы:

,

и т. д.; например, методом Ньютона:

с неким начальным значением , например,.

В общем случае(L=K ), обозначаяr = {r₁, …,r_k}, имеем еще более громоздкую нелинейную систему

R(r) = 0, гдеR = {R₁, R₂, …, R_K}

и итерационный процесс для ее решения

.

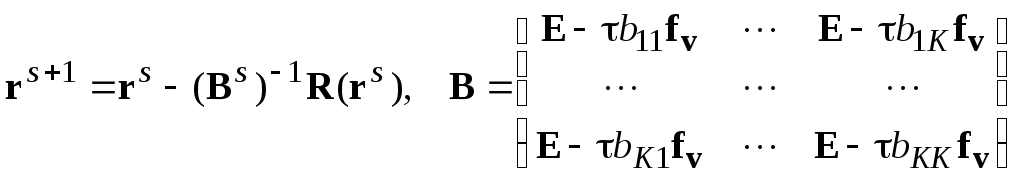2. Аппроксимация

Параметры схемы (неопределенные пока коэффициентыa₁, …,a_K;c₁, …,c_K; b₁₁, …,b_1K, …,b_K1, …,b_KK), конечно, не произвольны. Их (все или часть) находят, прежде всего, из условий аппроксимации, получаемых из разложения (21) в ряд в точкеt=tⁿ илиt =tⁿ⁺¹ с учетом (18) и его следствий

v_t = f(t, v),

(т. е. рассматривая аппроксимацию на решениях (18)).

Поскольку в (21) при r_kстоит множительτ, то в разложении правой части (21) нужно удерживать на один член ряда меньше, чем в левой. Индексnбудем опускать. Итак, левая часть (21):

Далее:

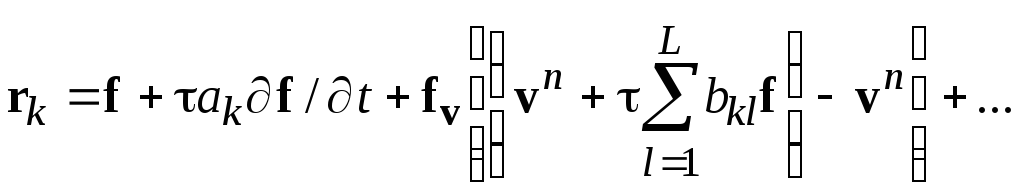
Если коэффициенты a_kвыбирать таким образом, чтобы

, (23)

то Подставляя эти разложения в (21) и группируя члены при одинаковых степеняхτ, получим (после деления на τ )

Очевидно, что при выполнении условия (вместе с (23))

(24)

обеспечивается 1-й порядок аппроксимации, при

(25)

(вместе с (23), (24)) — 2-й порядок аппроксимации. Условия 3-го порядка точности (вместе с (23) – (25)) есть

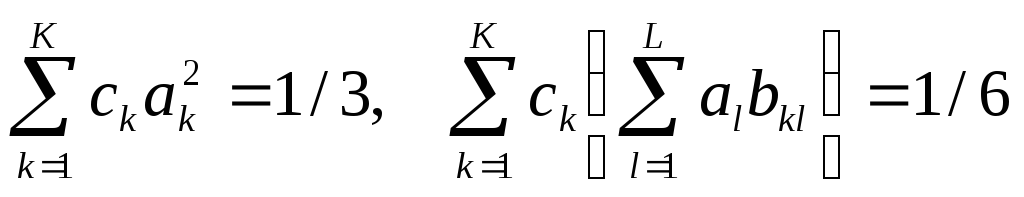, (26)

а условия 4-го порядка (вместе с (23) – (26)):

,

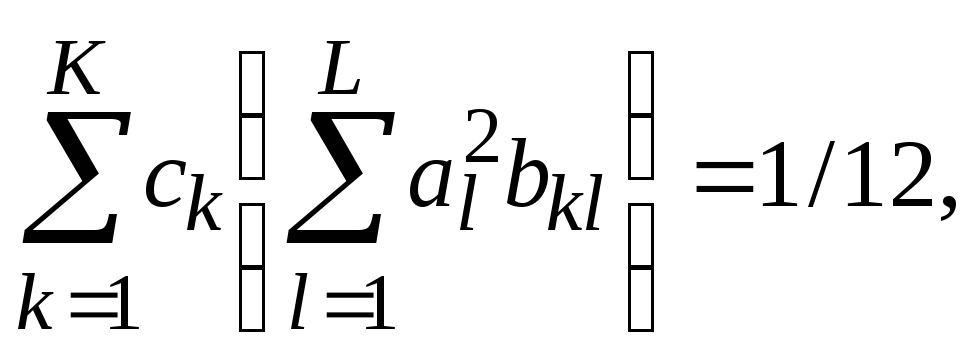(27)

.

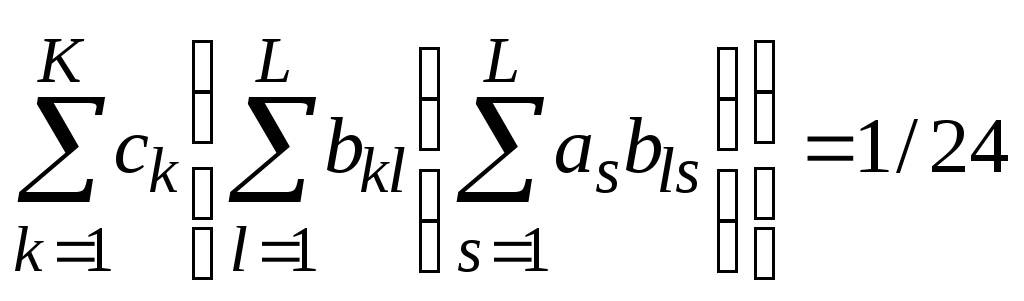Уравнения (23) – (27) составляют относительно неопределенных коэффициентов некоторую нелинейную систему. Очевидно, что привлекаемое число условий аппроксимации (т. е. порядок точности схемы рпри выполнении соответствующих условий гладкости) должно быть меньше числа отличных от нуля коэффициентов в (21), и соответствующая система должна быть разрешима. В частности, для явных схем, а для общих неявных схем.