4. Линейные многошаговые схемы (методы типа Адамса)

   1. Алгоритм и аппроксимация

Используя, как и в разделе 1.3, метод неопределенных коэффициентов и записывая линейную комбинацию вектор-функций vиfв некоторой последовательности равноотстоящих точекtⁿ,tⁿ⁺¹, …,t^n+k(=t^n+k–t^n+k=const), для линейных многошаговых методов получим следующее выражение:

. (43)

Из-за однородности (43), коэффициент при искомом значении v^n+kможно выбрать единичным:

а_K=1. (44)

Неопределенные коэффициенты a_k,b_k(k= 0, …,K ) из разложения (43) в ряд Тейлора в точкеt^n+K(илиtⁿ) связаны условиями аппроксимации (на решениях (18)):

, (45)

(обеспечивают 1-й порядок аппроксимации),

(46)

(обеспечивает 2-й порядок аппроксимации вместе с (45)),

…

(47)

(обеспечивает -й порядок аппроксимации на решениях (18) вместе с предшествующими условиями).

Схемы первого порядка аппроксимации малоинтересны, поэтому в дальнейшем будем рассматривать схемы второго или более высокого порядка точности. Если с учетом нормировки (44) и условий аппроксимации второго порядка точности (45), (46) исключить, например,

,

,

,

то оставшиеся свободными коэффициенты (если позволяет выбранное K > 2), можно принять за линейное пространство размерности 2(K–1), например, с евклидовой метрикой. Каждой точке в этом пространстве будет соответствовать некоторая разностная схема второго порядка точности, а условия более высокого порядка аппроксимации ((47) при= 3 и т. д.) после исключения в нихa_K,a_K–1,b_K,b_K–1, являясь относительно оставшихся свободными коэффициентовa_k,b_k(k=0 , …,K–2 ) линейными уравнениями

,

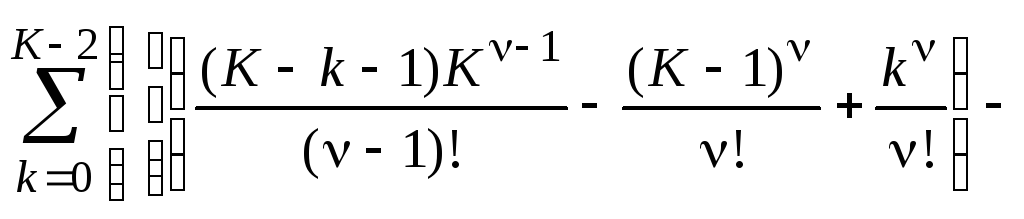
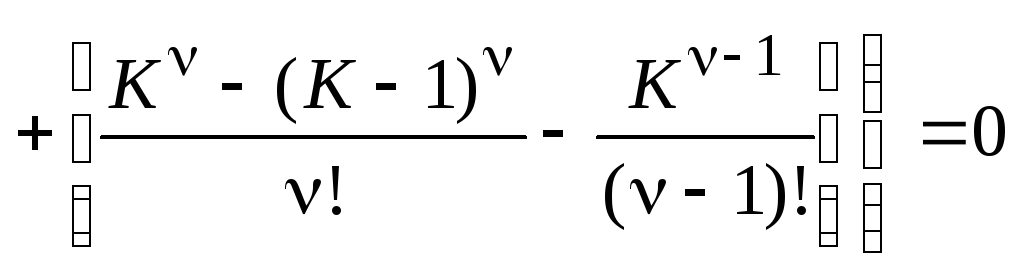образуют в этом пространстве соответствующую гиперплоскость схем третьего порядка аппроксимации. На пересечении двух таких гиперплоскостей ((47) при = 3 и= 4) будут расположены схемы с четвертым порядком аппроксимации и т. д., пока мы не исчерпаем все возможности для выбранногоK, т. е. пока не найдем единственную схему с наиболее высоким порядком аппроксимации (точку в этом пространстве).

В частности, при K=2 имеем:

a₂ = 1, a₁ = –1 – a₀,

b₂ = (1 + a₀ + 2b₀) /2, b₁ = (1 – 3a₀ – 4b₀) / 2, (48)

где a₀иb₀произвольны для схем 2-го порядка точности.

Условие 3-го порядка аппроксимации дает прямую в плоскости {a₀,b₀} с уравнением

5a₀ + 12b₀ + 1=0,

а единственной схемой 4-го порядка аппроксимации будет точка на этой прямой с координатами:

a₀=–1, b₀=1/3. (49)

2. Устойчивость

Как уже отмечалось, одной аппроксимации недостаточно для сходимости решений (43) к решениям исходной дифференциальной задачи даже в линейном случае (7). Нужно еще обеспечить устойчивость разностных схем (43). Для одного линейного уравнения, полагая f=v, из (43) получим

. (50)

Устойчивость разностных схем (50) будем исследовать на специальных решениях вида vⁿ=qⁿ. Тогда для определенияqимееммногочленустойчивостистепениKи уравнение

,

корни которого q_j,j= 1, 2,…,K(действительные или комплексные, в зависимости от,a_k,b_k) должны удовлетворять условиям устойчивости

|q()| ≤ 1, j= 1, …,K. (51)

Если в плоскости {Re , Im} область устойчивости, определяемая неравенствами (51), включает всю левую полуплоскость (т. е. (51) выполняется для всехс Re < 0), имеемA-устойчивую схему. Если эта область включает в себя заштрихованную на рис. 1.11а или 1.11б часть плоскости {Re, Im}, имеем жестко-устойчивую схему. Для действительныхиq_j() условия устойчивости схемы будут иметь вид –1 ≤ q_j() ≤ 1.Если это условие выполняется для всех:– <  ≤ 0, то схемаA-устойчива. Если

|q()|=0, j=1, 2, …,K, (52)

то схема будет L-устойчивой.