vysshaya_matematika_1001

В.И. Полтинников

ВЫСШАЯ МАТЕМАТИКА

Часть 1

Учебное пособие для бакалавров

Ростов-на-Дону 2012

1.ЛИНЕЙНАЯ АЛГЕБРА

1.1.Определители второго порядка

Определение. Определителем (детерминантом) второго по-

рядка называется выражение вида

где a11,a12,a21,a22 – элементы определителя. Элементы a11,a22 образуют главную диагональ определителя, а элементы a21,a12 – побочную диагональ.

Таким образом, определитель второго порядка равен разности между произведениями элементов, стоящих на главной и побочной диагоналях.

Определитель второго порядка содержит две строки и два столбца: элементы a11,a12 стоят в первой строке определителя, а

элементы a21,a22 – во второй строке; элементы a11,a21 стоят в пер-

вом столбце определителя, а элементы a12,a22 – во втором столбце.

Любой элемент определителя можно записать в виде aik , где индекс i указывет номер строки (i 1,2), а индекс k – номер столбца (k 1,2), на пересечении которых стоит рассматриваемый

элемент.

Обычно элементами определителя являются числа, тогда и сам определитель – это число.

ПРИМЕР.

2 3

2 7 5 ( 3) 14 15 29.

5 7

Но иногда элементами определителя могут быть и другие математические объекты, например функции.

ПРИМЕР.

1.2. Определители третьего порядка

Определение. Определителем (детерминантом) третьего порядка называется выражение вида

где a11,a12,a13,a21,a22,a23,a31,a32,a33 – элементы определителя. Элементы a11,a22,a33 образуют главную диагональ определи-

теля, а элементы a31,a22,a13 – побочную диагональ.

Определитель третьего порядка содержит три строки и три столбца: элементы a11,a12,a13 стоят в первой строке определителя,

элементы a21,a22,a23 стоят во второй строке определителя, а эле-

менты a31,a32,a33 – в третьей строке; элементы a11,a21,a31 стоят в первом столбце определителя, элементы a12,a22,a32 стоят во втором

столбце определителя, а элементы a13,a23,a33 – в третьем столбце.

Любой элемент определителя можно записать в виде aik , где индекс i указывет номер строки (i 1,2,3) , а индекс k – номер столбца (k 1,2,3), на пересечении которых стоит рассматриваемый

элемент.

Заметим, что определитель третьего порядка выражается в виде суммы, каждый член которой есть произведение трех элементов, взятых по одному и только по одному из каждой строки и каждого столбца.

Рассмотрим два правила составления указанной суммы (простое запоминание этого выражения затруднительно).

1. Правило треугольников.

Первые три слагаемых суммы (со знаком «+») представляют собой произведения элементов определителя, взятых по три так, как показано на нижеприведенной схеме слева (рис. 1.1). Для получения следующих трех слагаемых суммы (со знаком «–») нужно взять произведения элементов определителя, взятых по три так, как показано на нижеприведенной схеме справа (см. рис. 1.1).

4

Рис. 1.1. Правило треугольников вычисления определителя третьего порядка

ПРИМЕР.

5 1 2

3 2 4 5 2 ( 1) 1 4 6 3 ( 3) ( 2)

6 3 1

6 2 ( 2) 3 1 ( 1) ( 3) 4 5 119.

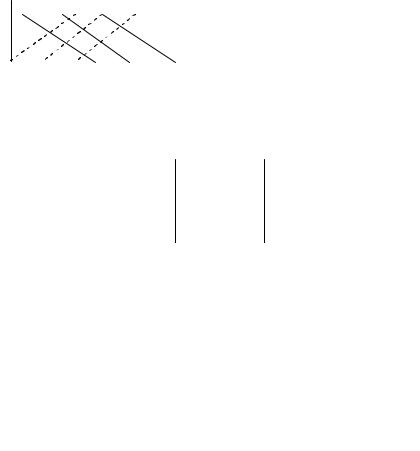
2.Правило Саррюса.

Напишем квадратную таблицу, соответствующую определителю третьего порядка, и припишем к ней справа еще раз первый и

5 2 ( 1) 1 4 6 ( 2) 3 ( 3) 6 2 ( 2) ( 3) 4 5 ( 1) 3 1 119.

1.3. Определители высшего порядка

Определение. Определителем (детерминантом) высшего

(n-го) порядка называется выражение вида

a11 a12 ... a1n

a21 a22 ... a2n ,

.....................

an1 an2 ... ann

где a11,a12,...,a1n;a21,a22,...,a2n;...;an1,an2,...,ann – элементы опре-

делителя. Элементы образуют главную диагональ определителя, а элементы an1,...,a1n – побочную диагональ.

Определитель n-го порядка содержит n строк и n столбцов. Обычно определитель считают определителем высшего порядка, если n 3.

Элементы a11,a12,...,a1n стоят в первой строке определителя,

элементы a21,a22,...,a2n стоят во второй строке определителя и т.д., а элементы an1,an2,...,ann – в последней, n-й, строке.

Элементы a11,a21,...,an1 стоят в первом столбце определите-

ля, элементы a12,a22,...,an2 стоят во втором столбце определителя и т.д., а элементы a1n,a2n,...,ann – в последнем, n-м, столбце.

Любой элемент определителя можно записать в виде aik , где индекс i указывет номер строки (i 1,2,...,n), а индекс k – номер столбца (k 1,2,...,n), на пересечении которых стоит рассматриваемый элемент.

6

Для записи правила вычисления определителя n-го порядка рассмотрим предварительно понятия минора и алгебраического дополнения.

Определение. Минором Mik элемента aik определителя

n-го порядка называется определитель (n-1)-го порядка, полученный из исходного определителя n-го порядка вычеркиванием i-й строки и k-го столбца.

ПРИМЕРЫ:

Определение. Алгебраическим дополнением Aik элемента aik определителя n-го порядка называется произведение знакового

Легко заметить, что знаковые множители соседних алгебраических дополнений чередуются (с плюса на минус или с минуса на плюс) при движении элемента по строке или при движении элемента по столбцу, а для элементов, стоящих на главной диагонали, знаковые множители алгебраических дополнений всегда положительны.

Например, знаковые множители для миноров элементов в определителе третьего порядка можно задать таблицей

.

Используя понятие алгебраического дополнения, сформули-

руем универсальное правило вычисления определителя n-го порядка (разложение по элементам строки или столбца), пригодное для вы-

числения определителя любого порядка:

Определитель n-го порядка равен сумме попарных произведений элементов какой-либо строки (столбца) на их алгебраические дополнения:

3( 1 6) 2( 5 12) 4( 15 6) 3 ( 7) 2 7 4 ( 21) 21 14 84 119.

2. Вычислить определитель

5 1 2

3 2 4

6 3 1

8

разложением по третьему столбцу.

Решение.

2( 9 12) 4( 15 6) 1(10 3) 2 ( 21) 4 ( 21) 1 7 42 84 7 119.

3.Вычислить верхний треугольный определитель четвертого

порядка

0 0 0 a44

т.е. определитель, все элементы которого, стоящие ниже главной диагонали, равны нулю.

Решение. Применяя последовательно универсальное правило вычисления определителя разложением по первому столбцу, получаем

Для вычисления нижнего треугольного определителя четвертого порядка, т.е. определителя, все элементы которого, стоящие выше главной диагонали, равны нулю, нужно применить последовательно универсальное правило вычисления определителя разложением по первой строке:

Очевидно, что для вычисления любого треугольного (как верхнего, так и нижнего) определителя n-го порядка справедлива формула:

9

т.е. треугольный определитель равен произведению его элементов, стоящих на главной диагонали.

Например,

1.4. Основные свойства определителей

Свойство 1. Определитель не меняет своего значения при транспонировании (замене всех его строк соответствующими столбцами).

ПРИМЕР.

Из данного свойства следует, что все свойства определителей, относящиеся к строкам определителя, справедливы для его столбцов, и наоборот.

Свойство 2. При перестановке местами каких-либо двух строк (столбцов) определитель меняет знак на противоположный.

ПРИМЕРЫ: