vysshaya_matematika_1001

нуля: a22 5 0. Переписываем разрешающую вторую строку без

изменения. Бывшей уже разрешающей первую строку также переписываем без изменения.

Однако в данном случае «обнулять» второй столбец не нуж-

но, так как в нем ниже разрешающего элемента a22 5 0 уже сто-

ят нули. Поэтому и остальные строки матрицы – третью и четвертую

– переписываем без изменения. Таким образом, матрица не изменилась.

На третьем шаге в качестве разрешающей (ведущей) строки выбираем третью строку, а в качестве разрешающего элемента выбираем диагональный элемент этой строки, так как он отличен от нуля: a33 2 0. Переписываем разрешающую третью строку без

изменения. Первая и вторая строки, которые уже были разрешающими, также переписываются без изменения.

«Обнуляем» третий столбец, для чего вместо четвертой строки записываем ее сумму с разрешающей третьей строкой:

Ñò ð.4 Ñò ð.4 Ñò ð.3.

Получаем эквивалентную матрицу

ранг которой равен четырем (количеству ненулевых строк). Тогда матрица, эквивалентная матрице системы, имеет вид

но ее ранг равен трем (количеству ненулевых строк).

Таким образом, на первом этапе метода Гаусса (прямой ход) установлено, что ранг матрицы системы не равен рангу расширенной матрицы системы

r(A) 3; r(AB ) 4; r(A) r(AB ).

Следовательно, система несовместна и не имеет решений.

41

Поднимаясь снизу вверх (обратный ход метода Гаусса), последовательно находим:

– из последнего r-го уравнения неизвестное xr r rr ;

–из (r 1)-го уравнения неизвестное xr 1 путем подстановки

вэто уравнение уже найденного неизвестного xr ;

–из i-го уравнения неизвестное xi при подстановке в него уже найденных величин xr ,xr 1,...,xi 1 ;

–и так далее до первого уравнения, из которого при подстановке в него уже найденных величин xr ,xr 1,...,x2 находим x1.

ПРИМЕР.

Найти методом Гаусса решение системы линейных уравнений

x1 2x2 3 x3 2,

3x1 4x2 3x3 0.

Решение.

1. Прямой ход метода Гаусса. Расширенная матрица системы имеет вид

Приведем ее с помощью элементарных преобразований к трапециевидной форме.

На первом шаге в качестве разрешающей (ведущей) строки выбираем первую строку, а в качестве разрешающего элемента выбираем диагональный элемент этой строки, так как он отличен от нуля: a11 1 0. Переписываем разрешающую первую строку без

изменения.

«Обнуляем» первый столбец, для чего:

– вместо второй строки записываем ее сумму с разрешающей первой строкой, умноженной на (-1): Ñò ð.2 Ñò ð.2 Ñò ð.1 ( 1) ;

43

–вместо третьей строки записываем ее сумму с разрешающей первой строкой, умноженной на (-1): Стр.3 Стр.3 Стр.1 ( 1);

–вместо четвертой строки записываем ее сумму с разрешающей первой строкой, умноженной на (-3): Стр.4 Стр.4 Стр.1 ( 3).

Получаем эквивалентную матрицу

Упростим ее с целью дальнейших преобразований, для чего:

– поменяем местами вторую и третью строки:

Стр.2 Стр.3;

– четвертую строку умножим на –(1/2): Стр.4 Стр.4 ( 12). Получаем эквивалентную матрицу

На втором шаге в качестве разрешающей (ведущей) строки выбираем вторую строку, а в качестве разрешающего элемента выбираем диагональный элемент этой строки, так как он отличен от нуля: a22 1 0 . Переписываем разрешающую вторую строку без

изменения. Бывшая уже разрешающей первая строка также переписывается без изменения.

«Обнуляем» второй столбец, для чего:

–вместо третьей строки записываем ее сумму с разрешающей второй строкой, умноженной на 3: Ñò ð.3 Ñò ð.3 Ñò ð.2 3;

–вместо четвертой строки записываем ее сумму с разрешающей второй строкой, умноженной на (-1): Ñòð.4 Ñòð.4 Ñòð.2 ( 1).

Получаем эквивалентную матрицу

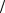
Упростим ее с целью дальнейших преобразований, для чего:

–третью строку умножим на –(1/14): Стр.3 Стр.3 ( 114);

–четвертую строку умножим на (1/7): Стр.4 Стр.4 (17). Получаем эквивалентную матрицу

На третьем шаге в качестве разрешающей (ведущей) строки выбираем третью строку, а в качестве разрешающего элемента выбираем диагональный элемент этой строки, так как он отличен от нуля: a33 1 0. Переписываем разрешающую третью строку без

изменения. Бывшие уже разрешающие первую и вторую строки также переписываем без изменения.

«Обнуляем» третий столбец, для чего:

– вместо четвертой строки записываем ее сумму с разрешающей третьей строкой, умноженной на (-1): Стр.4 Стр.4 Стр.3 ( 1).

Получаем эквивалентную матрицу

ранг которой равен трем (количеству ненулевых строк).

Тогда матрица, эквивалентная матрице системы, имеет вид

и ее ранг также равен трем (количеству ненулевых строк).

Таким образом, на первом этапе метода Гаусса (прямой ход) установлено, что ранг матрицы системы равен рангу расширенной матрицы системы

r(A) r(AB ) 3

45

и равен числу неизвестных. Следовательно, система совместна и имеет единственное решение.

Найдем далее это решение.

2. Обратный ход метода Гаусса. Полученная расширенная матрица системы

соответствует системе уравнений (нулевая строка может быть отброшена)

x1 2x2 3x3 2,

Заметим, что определитель системы

1 2 3

0 0 1

есть базисный минор третьего порядка расширенной матрицы AB , в который в качестве базисных столбцов входят столбцы, составленные из коэффициентов при неизвестных x1,x2,x3 .

Поднимаясь снизу вверх (обратный ход метода Гаусса), последовательно находим:

–из последнего 3-го уравнения неизвестное x3 1;

–из 2-го уравнения неизвестное x2 путем подстановки в это уравнение уже найденного неизвестного x3 1:

x2 4x3 4 4 1 4 0; x2 0.

– из 1-го уравнения неизвестное x1 при подстановке в него уже найденных неизвестных x3 1, x2 0 :

x1 2x2 3x3 2 2 0 3 1 2 1.

Таким образом, единственное решение системы: x1 1; x2 0; x3 1.

46

2. Ранг расширенной матрицы меньше числа неизвестных (r<n).

перенося в правые части уравнений все слагаемые, содержащие неизвестные xr 1,xr 2,...,xn . Тогда система принимает вид

зисными. Из данной системы легко найти выражения базисных неизвестных через свободные. Поскольку свободные неизвестные могут принимать любые значения, то в рассматриваемом случае r<n система является совместной и неопределенной: она имеет бесчисленное множество решений.

–из (r 1)-го уравнения неизвестное xr 1 путем подстановки

вэто уравнение уже найденного неизвестного xr ;

–из i-го уравнения неизвестное xi при подстановке в него уже найденных величин xr ,xr 1,...,xi 1 ;

47

– и так далее до первого уравнения, из которого при подстановке в него уже найденных величин xr ,xr 1,...,x2 находим x1.

ПРИМЕР.

Решить методом Гаусса систему линейных уравнений

2x1 x2 3 x3 2x4 4x5 1,

Решение.

1. Прямой ход метода Гаусса. Составим расширенную матрицу системы:

Приведем ее с помощью элементарных преобразований к трапециевидной форме.

На первом шаге в качестве разрешающей (ведущей) строки выбираем первую строку, а в качестве разрешающего элемента выбираем диагональный элемент этой строки, так как он отличен от нуля: a11 2 0. Переписываем разрешающую первую строку без

изменения.

«Обнуляем» первый столбец, для чего:

–вместо второй строки записываем ее сумму с разрешающей первой строкой, умноженной на (-2): Ñò ð.2 Ñò ð.2 Ñò ð.1 ( 2);

–вместо третьей строки записываем ее сумму с разрешающей первой строкой, умноженной на (-1): Ñò ð.3 Ñò ð.3 Ñò ð.1 ( 1) .

Получаем эквивалентную матрицу

На втором шаге в качестве разрешающей (ведущей) строки выбираем вторую строку, а в качестве разрешающего элемента вы-

бираем a23 1 0 , так как диагональный элемент этой строки ра-

вен нулю: a22 0. Переписываем разрешающую вторую строку без

48

изменения. Бывшей уже разрешающей первую строку также переписываем без изменения.

«Обнуляем» третий столбец (второй столбец уже «обнулен» в результате предыдущей операции), для чего вместо третьей строки записываем ее сумму с разрешающей второй строкой, умноженной на

ранг которой равен двум (количеству ненулевых строк).

Тогда матрица, эквивалентная матрице системы, имеет вид

и ее ранг также равен двум (количеству ненулевых строк).

Таким образом, на первом этапе метода Гаусса (прямой ход) установлено, что ранг матрицы системы равен рангу расширенной матрицы системы

rr(A) r(AB ) 2

именьше числа неизвестных n=5. Следовательно, система является совместной и неопределенной: она имеет бесчисленное множество решений.

Найдем далее эти решения.

2.Обратный ход метода Гаусса.

Полученная расширенная матрица системы

соответствует системе уравнений (нулевая строка может быть отброшена)

которая эквивалентна исходной системе уравнений.

49

В данном случае число неизвестных в системе n=5, а ранг r=2. Поэтому в качестве базисных неизвестных могут быть выбраны r=2 любых неизвестных, минор второго порядка для которых является базисным, т.е. отличен от нуля. Остальные n-r=3 неизвестных будут свободными.

Всего для матрицы системы можно составить (в этом легко убедиться хотя бы простым перебором) 10 миноров второго порядка, каждый из которых содержит два столбца при соответствующих неизвестных:

Видно, что все миноры, кроме первого, отличны от нуля, т.е. являются базисными. Значит, в качестве базисных неизвестных мож-

но взять любую пару, кроме неизвестных x1,x2 .

Выберем в качестве базисных неизвестных, например, x2,x3 .

Тогда x1,x4,x5 будут свободными неизвестными. Преобразуем систему уравнений

оставляя в левой части все слагаемые, содержащие базисные неизвестные x2,x3 и перенося в правые части уравнений все слагаемые,

содержащие свободные неизвестные x1,x4,x5 . Тогда система принимает вид

x2 3x3 1 2x1 2x4 4x5,