
vysshaya_matematika_1001
.pdf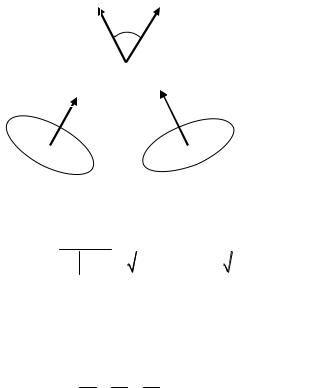
N2 |
|
N1 |
|
|
|
N1 |
|
|
|
|
|
N2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пл1 |
|
|
|
|
|
|
|
Пл2 |
|
|
|
|
|
|
||||
|
Рис. 3.10. Угол между плоскостями |
|
|
|
|
|
|
|
|
|||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(N ,N ) |
|
|
|
A A B B C C |
|
|
|
|||||||||
cos cos(N , N |
|
) |
1 |
2 |
|
|
|
1 |
2 |
1 |
2 |
|
1 2 |
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
2 |
|
N |
N |
2 |
|
|
A2 |
B2 |
C2 |
|
|
|
A2 |
B |
2 |
C2 |
|
|
|
|
1 |
|
|
|
1 |
1 |
1 |
|
|
2 |
2 |
2 |
|
|||
Условие перпендикулярности плоскостей совпадает с услови-
ем перпедикулярности нормальных векторов этих плоскостей:
A1A2 B1B2 C1C2 0,
а условием параллельности плоскостей является условие параллель-
ности их нормальных векторов, что выражаетcя пропорциональностью их соответствующих координат:
A1 B1 C1 .
A2 B2 C2
3.5. Прямая в пространстве
Параметрические уравнения прямой
Положение прямой в пространстве можно определить следующими данными:
1)точкой M0(x0,y0,z0), через которую проходит прямая,
называемой начальной точкой;
2)вектором s m,n, p , параллельным прямой, называе-
мым направляющим вектором прямой.
91
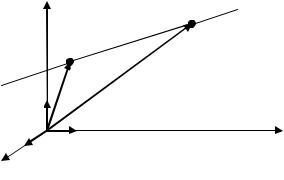
Составим сначала уравнение прямой в векторной форме.
Пусть даны начальный вектор r0 OM0 и направляющий вектор прямой s (рис. 3.11).
z
|
|
|
M0(x0 ,y0,z0) |
|
M(x, y,z) |
|
|
||||||||||
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rro |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
r |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
k |
rj |
|
|
|
|
|
|
|
|
|
|
y |
|||
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
O |
|
|
|
|
|
|
|
|
|
|
|||||
x |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.11. Уравнение прямой в пространстве в векторной форме |
|||||||||||||||||
Пусть |
|
OM r |
|
– |
радиус-вектор |
|
произвольной точки |
||||||||||
M(x,y,z) прямой. Тогда |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
OM OM0 M0M . |
|
|
|
|
|
|||||||
Так как M0M |
|
s , то существует такое число t, что M0M ts . |
|||||||||||||||
|
|||||||||||||||||
Полагая |
|
OM r, OM0 |
r0, M0M ts , |
получаем уравнение |
|||||||||||||
прямой в параметрической векторной форме: |
|
|
|
|
|||||||||||||
|
|
|
r r0 |
ts |
|
|
|
|
|
|
(3.5.1) |
||||||
Когда параметр t пробегает все вещественные значения |
|||||||||||||||||
t , конец вектора r |
пробегает все точки прямой. |
||||||||||||||||
Выразим векторы r, r0, |
s |
в координатной форме: |
|||||||||||||||
|
|
|
|
|
|
r |
|
|
|
|
|
|
k, |
||||
r OM xi yj zk, |
OM x i y j z |
||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
0 |
0 |
|
0 |
0 |
|
|
s m,n, p mi nj pk
и подставим в уравнение (3.5.1):
xi yj zk x0i y0 j z0k t(mi nj pk),
или
92

xi yj zk (x0 mt)i (y0 nt)j (z0 pt)k .
Приравнивая координаты при ортах i, j,k , получим пара-
метрические уравнения прямой в пространстве
x x0 mt, |
|
|
||
|
|
nt, |
где t . |
(3.5.2) |
y y0 |
||||
z z |
pt, |
|
|
|
|
0 |
|
|
|
Определение. Координаты m,n, p направляющего вектора |
||||
прямой s m,n, p |
называются направляющими коэффициентами |
|||
прямой.
ПРИМЕР.
Составить параметрические уравнения прямой, проходящей через точку M0(2;3; 1) параллельно вектору s 5;4;7 .
Решение.
Координаты начальной точки x0 2, y0 3, z0 1, направляющие коэффициенты искомой прямой m 5, n 4, p 7 . Параметрические уравнения прямой имеют вид:
x 2 5t,
y 3 4t,z 1 7t.
Канонические уравнения прямой
Преобразуем параметрические уравнения прямой (3.5.2) к
виду
x x0 t,m
y y0 t,
n
z z0 t,
p
откуда следуют канонические уравнения прямой
x x0 |
|
y y0 |
|
z z0 |
, |
(3.5.3) |
m |
n |
|
||||
|
|
p |
|
|||
93
проходящей через точку M0(x0,y0,z0) и имеющей направляющий вектор s m,n, p .
Заметим, что уравнение (3.5.3) может быть получено и из условия коллинеарности векторов M0M x x0,y y0,z z0 и s m,n, p , согласно которому соответствующие координаты коллинеарных векторов пропорциональны.
Уравнение прямой, проходящей через две данные точки
Пусть |
через |
две |
данные |
точки M1(x1,y1,z1) и |
||
M2(x2,y2,z2) |
требуется провести прямую. Возьмем на этой прямой |
|||||
произвольную |
точку |
M(x,y,z) |
и |
рассмотрим |
векторы |
|
M1M x x1,y y1,z z1 |
и M1M2 x2 |
x1,y2 y1,z2 |
z1 (рис. |
|||
3.12). Эти векторы коллинеарны (лежат на одной прямой), поэтому их соответствующие координаты пропорциональны:
x x1 |
|
y y1 |
|
z z1 |
. |
(3.5.4) |
x2 x1 |
y2 y1 |
|
||||
|
|
z2 z1 |
|
|||
Полученное уравнение называется уравнением прямой в про-
странстве, проходящей через две данные точки.
94
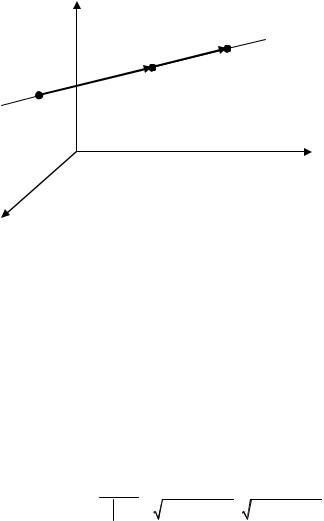
z
M2(x2, y2,z2)
M(x,y,z)
M1(x1,y1,z1)
O |
y |
x
Рис. 3.12. Уравнение прямой в пространстве, проходящей через две данные точки
Заметим, что данные уравнения можно рассматривать также и как канонические уравнения прямой с начальной точкой
M1(x1,y1,z1) |
и |
направляющим |
вектором |
прямой |
s M1M2 x2 x1,y2 y1,z2 z1 .
3.6. Угол между двумя прямыми в пространстве
Пусть две прямые заданы в пространстве параметрическими или каноническими уравнениями с направляющими векторами
s1 m1,n1, p1 и s2 m2,n2, p2 .
Очевидно, угол между прямыми будет равен углу между
их направляющими векторами, поэтому |
|
|
|
|
|
|
|
||||||||||
|
|
(s ,s ) |
|
|
|
m m n n |
p p |
2 |
|
. |
|||||||
cos cos(s |
,s |
|
) |
1 |
2 |
|
|
|
1 |
2 |
1 2 |
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
|
2 |
|
s |
s |
2 |
|
|
m2 |
n2 |
p2 |
|
m2 |
n2 |
p2 |
||
|
|
|
|
1 |
|
|
|
1 |
1 |
1 |
|
2 |
|
2 |
2 |
|
|
Условие перпендикулярности прямых совпадает с условием перпедикулярности направляющих векторов этих прямых
m1m2 n1n2 p1 p2 0,
95

а условием параллельности прямых является условие параллельно-
сти их направляющих векторов, что выражаетcя пропорциональностью их соответствующих координат:
m1 n1 p1 . m2 n2 p2
3.7. Угол между прямой в пространстве и плоскостью
Если через данную прямую провести плоскость, перпендикулярную к данной плоскости, то пересечение плоскостей даст прямую, которая называется проекцией данной прямой на данную плоскость (рис. 3.13). Угол между прямой и ее проекцией на данную плос-
кость называется углом между прямой и плоскостью. Всегда можно считать 0 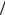 2.
2.
Если N – нормальный вектор плоскости, а s – направляющий вектор прямой (см. рис. 3.13), то
|
|
|
|
|
|
||
|
|
||||||
sin cos |
|
|
|
cos(s, N) |
|
0. |
|
2 |
|||||||
|
|
|
|
|
|
||
Модуль взят потому, что угол между векторами N и s может оказаться тупым.
ur
N
s
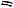

Рис. 3.13. Угол между прямой и плоскостью
Пусть заданы общее уравнение плоскости
Ax By Cz D 0, |
N A,B,C |
и канонические уравнения прямой
96
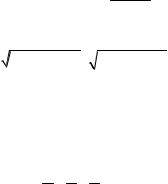
|
x x0 |
|
|
y y0 |
|
z z0 |
, |
s m,n, p . |
||||||||||||||||
|
|
|
n |
|
|
|
|
|||||||||||||||||
|
m |
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(N,s) |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
sin |
cos(s, N) |
|
|
|
|
|
|
|
|
|
, |
|
|
|||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
s |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
или |
sin |
|
|
|
|
Am Bn Cp |
|
|
|
|
|
|
|
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
 A2 B2 C2 m2 n2 p2
A2 B2 C2 m2 n2 p2
Если плоскость и прямая параллельны, то sin 0, и усло-
вие параллельности прямой и плоскости выражается равенством
Am Bn Cp 0.
Если N
 s, то прямая перпендикулярна к плоскости, и условия
s, то прямая перпендикулярна к плоскости, и условия
перпендикулярности прямой и плоскости выражаются равенствами
A B C . m n p
ПРАКТИЧЕСКИЕ ЗАДАНИЯ
Задание 1. Решение систем линейных уравнений (m=n)
Решить систему трех линейных уравнений с тремя неизвестными: 1) по формулам Крамера; 2) методом обратной матрицы; 3) методом Гаусса.
|
x1 2x2 x3 5, |
|
|
|
2x2 |
5x3 12, |
|||||||
1. |
|
|
3x2 3x3 1, |
2. |
|
|
|
|
|
|
|||
2x1 |
2x1 x2 3x3 7, |
||||||||||||
|
|
|
x 5x 9. |
|
x x x 4. |
||||||||
|
|
|
|
2 |
3 |
|
|
|
|
1 |
|
2 |
3 |
|
|
3x1 x2 3x3 10, |
|
x1 |
|
2x3 5, |
|||||||
3. |
|
|
2x2 |
x3 4, |
4. |
|
|
2x2 5x3 10, |
|||||
|
|
2x1 |
|||||||||||
|
|
2x |
x 3x 3. |
|
3x |
2x 2x 1. |
|||||||
|
|
|
1 |
|
2 |
3 |
|
|
1 |
|
|
2 |
3 |
|
2x1 |
x2 |
6x3 |
15, |
|
x1 x2 x3 0, |
|||||||
5. |
3x x |
2 |
x 2, |
6. |
3x 4x |
2 |
3x 1, |
||||||
|
|
1 |
|
|
3 |
|
|
1 |
|
|
3 |
||
|
x |
|
|
3x 7. |
|
|
|
2x 3x 8. |
|||||
|
|
1 |
|
|
|
3 |
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
97 |
|
|
|
|
|
|
|
2x1 x2 x3 1, |
|
3x1 2x2 |
5, |
||||||
7. |
|
|
3x3 7, |
8. |
|
|
2x2 x3 1, |
|||
x1 |
x1 |
|||||||||
|
|
x |
x 3x 6. |
|
x |
|
3x x 0. |
|||
|
|
1 |
2 |
3 |
|
1 |
|
2 |
3 |
|
|
|
x1 3x2 x3 2, |
|
x1 3x2 |
4, |
|||||
9. |
|
x1 |
2x2 x3 |
11, |
|
|
3x1 |
2x2 |
x3 3, |
|
|
10. |
|||||||||
|
2x x |
1. |
|
|
2x |
x x 3. |
||||
|
|
|
1 2 |
|
|
|
|
1 |
2 |
3 |
Задание 2. Решение систем линейных уравнений (m<n)
Применяя метод Гаусса, решить систему линейных уравне-
ний.
|
4x1 |
17x2 6x3 |
5x4 |
3x5 26, |
|||||||
|
|
|
x2 2x3 x4 2x5 2, |
||||||||
1. |
|
|
|||||||||
|
|
15x2 9x3 4x4 x5 9, |
|||||||||
|
3x1 |
||||||||||
|
4x |
15x 2x |
3x |
x |
|
30. |
|||||
|
|
1 |
|
2 |
|
3 |
|
4 |
5 |
|
|
|
2x1 |
9x2 |
4x3 |
3x4 |
3x5 |
83, |
|||||
|
|
|
7x2 |
2x3 |
x4 |
4x5 |
57, |
||||
3. |
2x1 |
||||||||||
|
|
6x2 |
2x3 |
2x4 |
|
|
|
35, |
|||
|
7x1 |
|
|
|
|||||||
|
x 19x |
12x |
|
5x |
2x |
|
188. |
||||
|
|
1 |
2 |
3 |
|
4 |
5 |
|
|||
|
2x1 10x2 |
|
|
4x4 2x5 6, |
|||||||
5. |
4x 9x |
10x |
|
3x |
x |
21, |
|||||
|
1 |
2 |
|
3 |
|
4 |
|
5 |
|
||
|
2x1 7x2 |
|
|
|
x4 3x5 3, |
||||||
|
|
|
4x 5x 4x 3x 6. |
||||||||
|
|
|
2 |
|
3 |
|
|
4 |
5 |
||
|
3x1 |
8x2 |
5x3 |
|
x4 |
8x5 14, |
|||||
7. |
4x |
7x |
14x |
|
5x |
3x |
15, |
||||
|
1 |
2 |
|
3 |
|
4 |
|
5 |
14, |
||
|
|
x 2x |
3x |
|
x |
2x |
|||||
|
1 |
2 |
|
3 |
|
4 |
|
5 |
|
||
|
|
|
x2 12x3 5x4 9x5 |
15. |
|||||||
|
|
|
|||||||||
|
8x1 |
5x2 |
10x3 |
3x4 |
5x5 |
14, |
||
|
|
x1 |
5x2 |
3x3 |
|
2x4 7x5 |
15, |
|
2. |
|
|||||||
|
|
2x2 |
2x3 |
x4 |
6x5 |
12, |
||
|
3x1 |
|||||||
|
4x |
2x |
11x |
6x |
6x |
11. |
||
|
|
1 |
2 |
3 |
|
4 |
5 |
|
|
5x1 |
5x2 |
2x3 |
x4 3x5 |
21, |
||
|
5x |
6x |
4x |
x |
4x |
20, |
|
4. |
1 |
2 |
3 |
4 |
5 |
|
|
|
7x1 14x2 25x3 2x4 7x5 6, |
||||||
|
2x 10x 25x |
x |
3x |
16. |
|||
|
|
1 |
2 |
3 |
4 |
5 |
|
|
x1 2x2 x3 |
x4 3x5 5, |
|||||
|
|
|
18x2 |
5x3 3x4 2x5 59, |
|||
6. |
x1 |
||||||
|
|
2x |
x |
x |
17, |
||
|
3x |
||||||
|
|
1 |
|
3 |
4 |
5 |
|
|
4x 22x 5x |
5x 52. |
|||||
|
|
1 |
2 |
3 |
|
5 |
|
|
8x1 26x2 |
4x3 |
2x4 x5 |
52, |
|||
8. |
3x |
x 2x |
x 3x 1, |
||||
|
1 |
2 |
3 |
|
4 |
5 |
|
|
2x1 |
2x2 x3 2x4 2x5 4, |
|||||
|
|
|
|
x3 |
x4 2x5 57. |
||
|
3x1 29x2 |
||||||
98
|
|
|
5x2 9x3 3x4 |
x5 33, |
3x1 |
7x2 |
7x3 |
2x4 3x5 |
40, |
|||||||||||
|
|
|
5x2 |
|
4x3 |
x4 |
2x5 |
33, |
|
|
8x2 10x3 |
3x4 |
x5 |
38, |
||||||
9. |
2x1 |
x1 |
||||||||||||||||||
|
2x |
x |
5x 2x |
3x |
|
10. |
|
4x 2x |
3x |
x 2x |
25, |
|||||||||
|
|
3, |
|
|||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
|
|
|
1 |
2 |
3 |
|
4 |
|
5 |
|
|
|||
|
|
|
x |
|
|
|
4x |
|
3. |
2x |
3x |
6x |
|
2x |
|
4x 23. |
||||
|
|
|
2 |
|
|
5 |
|
|
|
1 |
2 |
3 |
|
4 |
|
5 |
|
|||
|
|
|
Задание 3. Разложение вектора по базису |
|
|
|
|
|||||||||||||
|
|
|
Даны |
векторы |
|
a(a1;a2;a3), |
b(b1;b2;b3), |
c(c1;c2;c3) |
и |
|||||||||||
d(d1;d2;d3) |
в некотором базисе. Показать, что векторы a,b,c |
обра- |
||||||||||||||||||
зуют базис, и найти координаты вектора d |
в этом базисе. |
|
|
|
||||||||||||||||
1.a(1;2;3), b( 1;3;2), c(7; 3;5), d(6;10;17).
2.a(4;7;8), b(9;1;3), c(2; 4;1), d(1; 13; 13).
3.a(8;2;3), b(4;6;10), c(3; 2;1), d(7;4;11).
4.a(10;3;1), b(1;4;2), c(3;9;2), d(19;30;7).
5.a(2;4;1), b(1;3;6), c(5;3;1), d(24;20;6).
6.a(1;7;3), b(3;4;2), c(4;8;5), d(7;32;14).
7.a(1; 2;3), b(4;7;2), c(6;4;2), d(14;18;6) .
8.a(1;4;3), b(6;8;5), c(3;1;4), d(21;18;33).
9.a(2;7;3), b(3;1;8), c(2; 7;4), d(16;14;27).
10.a(7;2;1), b(4;3;5), c(3;4; 2), d(2; 5; 13) .
Задание 4. Аналитическая геометрия и векторная алгебра на плоскости
Даны вершины A(x1,y1), B(x2,y2), C(x3,y3) треугольника.
Найти: 1) длину стороны BC; 2) площадь треугольника; 3) уравнение стороны BC; 4) уравнение высоты, проведенной из вершины A; 5) длину высоты, проведенной из вершины A; 6) уравнение биссектрисы внутреннего угла B; 7) угол B. Сделать чертеж.
1. |
A(4;1), B(0; 2), C( 5;10). |
2. |
A( 7;3), B(5; 2), C(8;2). |
3. |
A(5; 1), B(1; 4), C( 4;8). |
4. |
A( 14;6), B( 2;1), C(1;5). |
5. |
A(6;0), B(2; 3), C( 3;9). |
6. |
A( 9;2), B(3; 3), C(6;1). |
|
|
99 |
|
7. |
A(7; 4), |
B(3; 7), C( 2;5). |
8. A( 8;4), B(4; 1), C(7;3). |
||
9. |
A(3; 3), |
B( 1; 6), C( 6;6). |
10. A( 6;5), B(6;0), C(9;4). |
||
|
|
|
Задание 5. Аналитическая геометрия |
|
|
|
|
|
и векторная алгебра в пространстве |
|
|
|
Даны |
вершины A1(x1,y1,z1), A2(x2,y2,z2), |
A3(x3,y3,z3), |
||
A4(x4,y4,z4) |
пирамиды. |
|
|
||
|
Найти: 1) длину ребра A1A2 ; 2) угол между ребрами A1A2 и |
||||
A1A4 ; 3) угол между ребром A1A4 |
и гранью A1A2A3 ; 4) площадь гра- |
||||
ни |
A1A2A3 ; 5) объем пирамиды; 6) уравнения прямых |
A1A2 и A1A4 ; |
|||
7) |
уравнения плоскостей A1A2A3 |
и A1A2A4 ; 8) угол между плоско- |
|||
стями A1A2A3 |
и A1A2A4 . |
|
|
||
1.A1(3;1;4), A2( 1;6;1), A3( 1;1;6), A4 (0;4; 1).
2.A1(3;3;9), A2(6;9;1), A3(1;7;3), A4(8;5;8).
3.A1(3;5;4), A2(5;8;3), A3(1;9;9), A4(6;4;8).
4.A1(2;4;3), A27;6;3), A3(4;9;3), A4(3;6;7) .
5.A1(9;5;5), A2( 3;7;1), A3(5;7;8), A4 (6;9;2).
6.A1(0;7;1), A2(4;1;5), A3(4;6;3), A4(3;9;8).
7.A1(5;5;4), A2(3;8;4), A3(3;5;10), A4 (5;8;2).
8.A1(6;1;1), A2(4;6;6), A3(4;2;0), A4 (1;2;6).
9.A1(7;5;3), A2(9;4;4), A3(4;5;7), A4(7;9;6).
10.A1(6;6;2), A2(5;4;7), A3(2;4;7), A4(7;3;0).
Рекомендуемая литература
1. Бугров Я.С. Высшая математика. В 3 т.: учеб. для вузов. Т.1: Элементы линейной алгебры и аналитической геометрии / Я.С. Бугров, С. М. Никольский; под. ред. В.А. Садовничего. 5-е изд.,
стер. – М.: Дрофа, 2003. – 284 с.
2. Привалов И.И. Аналитическая геометрия: учебник / И.И. Привалов. 35-е изд., стер. – СПб.: Лань, 2005. – 299 с.
100
