vysshaya_matematika_1001

а на плоскости –

x1x2 y1y2 0.

ПРИМЕР. Найти скалярное произведение векторов a 2; 3; 1 , b 1; 2;8 .

Решение. (a,b) 2 1 ( 3) ( 2) ( 1) 8 2 6 8 0.

В данном примере скалярное произведение векторов a и b равно нулю, следовательно, эти векторы ортогональны (перпендикулярны).

Рассмотрим некоторые задачи, решаемые скалярным произведением.

1. Нахождение угла между векторами. Так как ска-

2. Направляющие косинусы.

Определение. Направляющими косинусами вектора a на-

зываются косинусы углов, образованных этим вектором с осями прямоугольной декартовой системы координат (рис. 2.11).

71

z

Из полученных формул после возведения обеих частей каждого равенства в квадрат и почленного сложения получаем соотношение между направляющими косинусами:

cos2 cos2 cos2 1.

cos2 cos2 1.

2.11.Векторное произведение векторов

вкоординатной форме

Пусть разложения векторов a и b по ортонормированному

Из определения векторного произведения векторов для ортонормированного базиса имеем (см. рис. 2.11):

3) i, j,k образуют правую тройку.

Аналогично вычисляются и другие векторные произведения базисных ортов:

Тогда на основании свойств векторного произведения векторов, а также правил сложения векторов и умножения вектора на число получаем

ров в координатной форме можно записать в виде определителя

который нужно вычислять разложением по первой строке. ПРИМЕР.

Решение.

2.12.Смешанное произведение векторов

вкоординатной форме

Пусть разложения векторов a,b,c по ортонормированному

Из определения смешанного произведения векторов, выражения для векторного произведения векторов в координатной форме и соотношений между базисными ортами для ортонормированного базиса имеем:

(a,b,c) (a b) c

((y1z2 z1y2)i (x1z2 z1x2)j (x1y2 y1x2)k) (x3i y3 j z3k)

(y1z2 z1y2)x3 (x1z2 z1x2)y3 (x1y2 y1x2)z3.

Последнюю сумму можно рассматривать как разложение по третьей строке определителя:

x3 y3 z3

Условие компланарности трех векторов a,b,c в координат-

ной форме выразится равенством

x1 y1 z1

x2 y2 z2 0.

x3 y3 z3

ПРИМЕР.

Определить, являются ли компланарными векторы a 2;0; 1 , b 3; 2;6 , c 4; 3;5 .

Решение. Для ответа на поставленный вопрос нужно вычислить смешанное произведение данных векторов:

Следовательно, данные векторы некомпланарны.

75

Вычтем из уравнения (3.1.1) почленно полученное равенство:

M(x,y) удовлетворяют уравнению (3.1.1). Тогда уравнение (3.1.2) можно представить в форме

(N,M0M) 0.

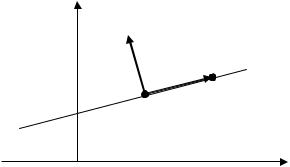
Вектор M0M перпендикулярен вектору N и, значит, все точки M(x,y) лежат на прямой, проходящей через точку M0 (рис.

3.1) перпендикулярно к вектору N .

Обратно, для любой точки M(x,y), лежащей на указанной

прямой, вектор M0M перпендикулярен вектору N .

Следовательно, уравнение (3.1.1) есть уравнение прямой. Определение. Уравнение вида

Ax By C 0

называется общим уравнением прямой.

Вектор N A,B , перпендикулярный к прямой (3.1.1), называется нормальным вектором этой прямой.

y

ur

N

M

M0

Рис. 3.1. Общее уравнение прямой

77

Отметим частные случаи положения прямой относительно системы координат.

1. Если в уравнении (3.1.1) свободный член C 0, т.е.

Ax By 0,

то прямая проходит через начало координат, так как координаты точки O(0;0) удовлетворяют уравнению.

2. Если A 0, то нормальный вектор N 0,B , B 0, параллелен оси ординат, значит, сама прямая параллельна оси абсцисс

3. Если B 0, то нормальный вектор N A,0 , A 0, параллелен оси абсцисс, значит, сама прямая параллельна оси ординат

Заметим, что уравнение (3.1.1) можно умножить на любое число, не равное нулю, и полученное уравнение будет уравнением той же самой прямой.

Параметрические уравнения прямой

Положение прямой на плоскости можно определить следующими данными:

1)точкой M0(x0,y0), через которую проходит прямая, назы-

ваемой начальной точкой;

2)вектором s m,n , параллельным прямой, называемым

направляющим вектором прямой.

Составим сначала уравнение прямой в векторной форме.

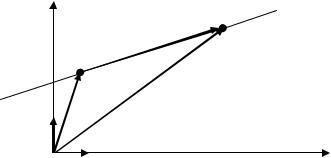
Пусть даны начальный вектор r0 OM0 и направляющий вектор прямой s (рис. 3.2).

78

прямой. Тогда

OM OM0 M0M .

Так как M0M s , то существует такое число t, что M0M ts .

Когда параметр t пробегает все вещественные значенияt , конец вектора r пробегает все точки прямой.

Выразим векторы r, r0, s в координатной форме:

r OM xi yj, r0 OM0 x0i y0 j, s m,n mi nj

иподставим в уравнение (3.1.3):

xiyj x0i y0 j t(mi nj), или xi yj (x0 mt)i (y0 nt)j .

Приравнивая координаты при ортах i и j , получим пара-

метрические уравнения прямой на плоскости:

Определение. Координаты m и n направляющего вектора прямой s m,n называются направляющими коэффициентами

прямой.

ПРИМЕР.

Составить параметрические уравнения прямой, проходящей

уравнения прямой имеют вид:

x 2 5t,

y 3 4t.

Каноническое уравнение прямой

Преобразуем параметрические уравнения прямой (3.1.4) к виду

тор s m,n .

Заметим, что уравнение (3.1.5) может быть получено и из ус-

ловия коллинеарности векторов M0M x x0,y y0 и s m,n ,

согласно которому соответствующие координаты коллинеарных векторов пропорциональны.

Уравнение прямой, проходящей через две данные точки

Пусть через две данные точки M1(x1,y1) и M2(x2,y2) требуется провести прямую. Возьмем на этой прямой любую (текущую)

точку M(x,y) и рассмотрим векторы M1M x x1,y y1 и

80