2.3 Застосування теореми Гаусса Приклад 2.5

Електростатичне поле ізольованої зарядженої провідної кулі

Нехай куля радіуса має заряд(рис.2.5). Всередині провідного тіла електростатичне поле відсутнє. Оскільки поле зовні кулі має сферичну симетрію, то можна застосувати інтегральну форму теореми Гаусса (1.16).

Обведемо заряджену кулю сферичною поверхнею радіусомі запишемо теорему Гаусса

.

В зв’язку з симетрією напруженість поля для усіх точок сфери має одне і те ж саме значення і направлена нормально до поверхні сфери, тому векториізбігаються за напрямком і можна записати

.

Рисунок 2.5 Оскількився поверхня сфери радіуса, дорівнює, то

і

.

Даний вираз збігається з виразом напруженості точкового заряду, якщо вважати його розташованим в центрі провідної кулі.

Потенціал поля в будь-якій точці зовні кулі визначається

.

Якщо шлях інтегрування вибрати по радіусу , то в зв’язку з тим що векториізбігаються за напрямком

,

де – постійна інтегрування.

Прийнявши потенціал точки, яка віддалена в нескінченність , рівним нулю, отримаємоі тоді

. (2.4)

Потенціал самої кулі визначається

.

Ємність відокремленої зарядженої кулі становить

.

Ємність земної кулі при

.

Приклад 2.6

Мильна кулька, радіусом з товщиною стінкизаряджена до потенціалулопнула і перетворилась в краплю, яка має об’єм, що дорівнює об’єму стінки кульки. Визначити потенціал краплі, якщо на ній зберігся той самий заряд.

Розв’язування. Позначимо заряд мильної кульки через і використаємо (2.4) для його визначення

.

Знайдемо об’єм стінок мильної кульки

.

Вважаючи, що крапля має сферичну форму, знайдемо її радіус

,

звідки

.

Потенціал краплі

.

Приклад 2.7

Поле діелектричної зарядженої кулі

Нехай в пустоті розміщено кулю радіусом з діелектричною проникністю, зарядякої рівномірно розподілений по об’єму (рис.2.6).

Взв’язку з тим, що куля і середовище, в якому вона знаходиться, різні, застосуємо теорему Гаусса два рази – всередині і зовні кулі.

Проведемо сферичну поверхню радіусом і запишемо теорему Гаусса

.

Рисунок 2.6 Всередині цієї поверхні знаходиться частина заряду рівна заряду, який знайдемо через об’ємну густину заряду

,

.

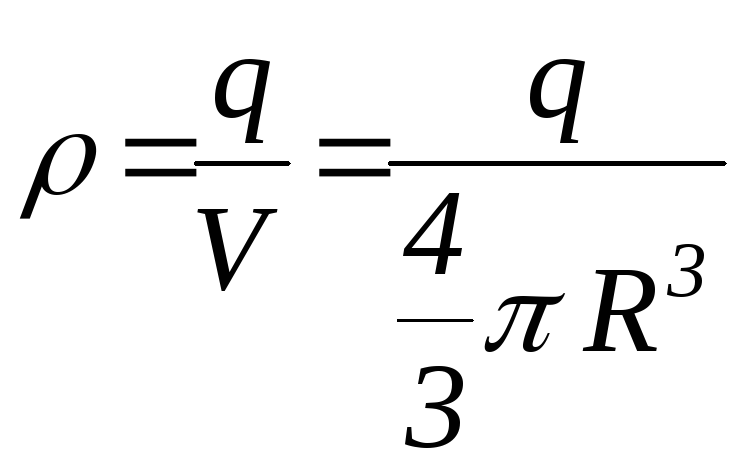Як і в попередньому прикладі

,

тому

і

. (2.6)

Всередині кулі напруженість лінійно зростає від центра кулі до її поверхні.

Для визначення напруженості зовні кулі опишемо заряд сферичною поверхнею радіусом . Застосувавши ті ж самі міркування, що і раніше, отримаємо

, ,,.

Поле зовні кулі таке ж саме, як і поле точкового заряду , зосередженого в центрі кулі.

Знайдемо закон зміни потенціалу в полі зовні кулі

,

для чого проінтегруємо за радіусом

,

де – постійна інтегрування.

Прийнявши потенціал нескінченно віддаленої точки рівним нулю, отримаємо

і (2.7)

Потенціал поля всередині кулі визначається

.

Постійну інтегрування знаходимо із граничних умов. На межі розділу середовищ потенціальна функція неперервна, тому

,

тобто

.

Звідки

і

.

На рис.2.7 наведені графіки зміни потенціалу і напруженості в залежності від відстані .

Рисунок 2.7

На межі розділу середовищ напруженість поля має розрив, в зв’язку з тим, що виконується гранична умова

.

Знайдемо енергію електростатичного поля, використавши для цього (1.68). Енергія поля всередині кулі визначається

.

Елемент об’єму представимо як добуток сферичної поверхні на елемент радіуса

.

Отже

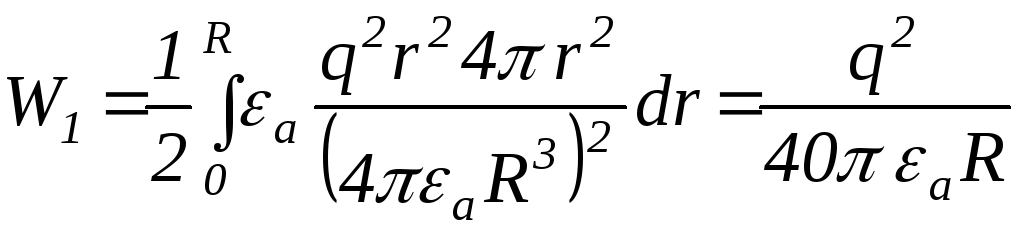. (2.8)

Енергія поля зовні кулі

або

. (2,9)

Загальна енергія всього поля визначається

. (2.10)

Якщо мати на увазі, що , то (2.10) показує, що більша частина енергії припадає на поле в охоплюючому кулю просторі.