
Расчетно-проектировочные работы и примеры их выполнения. Методическое пособие для студентов дневных / Основныезадачи 1-го семестра
.pdf
– участок BC:
BC |
M BC a |
|
|
|
|
1,724 103 0,3 |
|
|
|
5,21 10 3 |
(рад.); |
|||
GI (pBC) |
7,8 1010 127,2 10 8 |
|||||||||||||
|
|
|
|
|
|
|
||||||||
– участок CD: |
|
|
|
|
|
|
|
|
|
|
||||
CD |
MCDb |
|
|
|
|
0,276 103 0,3 |
|
1,73 10 3 |
(рад.); |
|||||
GI (pCD) |
|
|
7,8 1010 61,4 10 |
8 |
||||||||||
|
|
|
|
|
|
|
|
|
||||||
– участок DE: |
|
|
|
|
|
|
|
|
|
|
||||
DE |
M |
DE |
b |
|
|
|
|
3,873 103 0,2 |
|
|
|
4,61 103 (рад.). |
||
GI (pDE) |
|
|
|
7,8 1010 209,9 10 8 |
|
|||||||||
|
|
|
|
|
|
|
|
|||||||
Определяем углы закручивания характерных сечений вала относительно левой заделки.
AC AB BC 1,13 10 3 5,21 10 3 6,34 10 3 (рад.).AD AC CD 6,34 10 3 1,73 10 3 4,61 10 3 (рад.).
AE AD DE 4,61 10 3 4,61 10 3 0.
Угол поворота сечения E относительно сечения A равен нулю, то есть условие совместности деформаций выполняется и момент MA найден верно.
8. Проверим вал по условиям прочности и жесткости. Условие прочности при кручении: max [ ].
max 61,2(МПа) [ ] 90 (МПа). |
|
|
Условие прочности выполняется. |
|
|
Условие жесткости имеет вид |
[ ]. |
|
|
l |
|
Максимальный относительный угол закручивания будет на участке стержня, на котором действует максимальное касательное напряжение.
max |
|
DE |
|
DE |
|
4,61 |
10 3 |
0,023(рад./м) [ ] 0,025 . |
|
||||||||
|
|
|
|
|||||
|
|
|
b |
|
0.2 |
|
||
Условие жесткости выполняется. Вал удовлетворяет эксплуатационным требованиям.
101
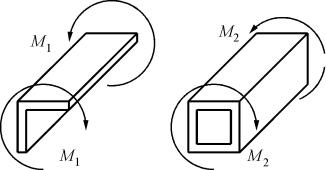
ЗАДАЧА № 3
Два тонкостенных стержня нагружены постоянными по длине крутящими моментами. Выполнить проверку по условию прочности, для стержня замкнутого профиля построить эпюру касательных напряжений в поперечном сечении. Расчетные схемы изображены на рис. 3.34, формы поперечных сечений – на рис. 3.35 – 3.37, исходные данные для расчета – в табл. 3.4.
Рис. 3.34. Расчетные схемы к задаче 3.
|
|
|
|
|
|
|
|
|
|
|
|
Табл. 3.6. |
|
|
|
|
Исходные данные к задаче 3 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
№ |
Крутящие |
|
Размеры стержня, |
Толщина элементов |
[ ], |
|
|||||||
моменты, Н м |
|
|
см |
|
стержня, мм |
|
|
||||||
вар. |
|
|
|
|
МПа |
|
|||||||
M1 |
M2 |
|
a |
|
b |
1 |
|
2 |
|
3 |
|
||
|
|
|
|
|
|
|
|||||||
1 |
10 |
500 |
|
4 |
|
5 |
1 |
|
1,2 |
|
1,5 |
80 |
|
2 |
15 |
800 |
|
5 |
|
6 |
1 |
|
1,5 |
|
1,8 |
70 |
|
3 |
20 |
1000 |
|
5 |
|
7 |
1,2 |
|
1,5 |
|
1,8 |
60 |
|
4 |
30 |
1200 |
|
6 |
|
8 |
1,2 |
|
1,5 |
|
2,0 |
90 |
|
5 |
40 |
1800 |
|
7 |
|
10 |
1,3 |
|
1,5 |
|
1,8 |
100 |
|
6 |
50 |
2500 |
|
8 |
|
10 |
1,5 |
|
1,8 |
|
2,0 |
120 |
|
7 |
60 |
3000 |
|
8 |
|
12 |
1,5 |
|
2,0 |
|
2,5 |
80 |
|
8 |
70 |
3200 |
|
10 |
|
12 |
1,8 |
|
2,0 |
|
2,5 |
70 |
|
9 |
80 |
4000 |
|
10 |
|
15 |
2,0 |
|
2,5 |
|
3,0 |
60 |
|
10 |
90 |
4200 |
|
10 |
|
20 |
2,0 |
|
3,0 |
|
3,5 |
90 |
|
11 |
100 |
4500 |
|
12 |
|
15 |
2,4 |
|
2,6 |
|
2,8 |
100 |
|
12 |
120 |
5000 |
|
12 |
|
18 |
2,4 |
|
2,8 |
|
3,0 |
120 |
|
13 |
150 |
5500 |
|
15 |
|
15 |
2,5 |
|
3,0 |
|
3,5 |
80 |
|
14 |
175 |
6000 |
|
15 |
|
18 |
2,5 |
|
3,5 |
|
4,0 |
70 |
|
15 |
180 |
6500 |
|
15 |
|
20 |
3,0 |
|
3,5 |
|
4,0 |
60 |
|
16 |
200 |
7000 |
|
16 |
|
20 |
3,0 |
|
4,0 |
|
5,0 |
90 |
|
17 |
220 |
7500 |
|
16 |
|
24 |
3,0 |
|
4,0 |
|
6,0 |
100 |
|
18 |
250 |
8000 |
|
16 |
|
25 |
3,5 |
|
4,0 |
|
4,5 |
120 |
|
19 |
275 |
8500 |
|
18 |
|
20 |
3,5 |
|
4,5 |
|
5,0 |
80 |
|
20 |
300 |
9000 |
|
18 |
|
25 |
4,0 |
|
5,0 |
|
6,0 |
70 |
|
21 |
320 |
10000 |
|
18 |
|
30 |
4,0 |
|
4,5 |
|
5,0 |
60 |
|
22 |
340 |
12000 |
|
20 |
|
25 |
4,5 |
|
5,0 |
|
6,0 |
90 |
|
23 |
350 |
15000 |
|
20 |
|
28 |
4,5 |
|
6,0 |
|
6,5 |
100 |
|
24 |
375 |
16000 |
|
20 |
|
30 |
4,5 |
|
6,0 |
|
7,0 |
120 |
|
25 |
400 |
17000 |
|
25 |
|
25 |
5,0 |
|
6,0 |
|
7,0 |
80 |
|
102
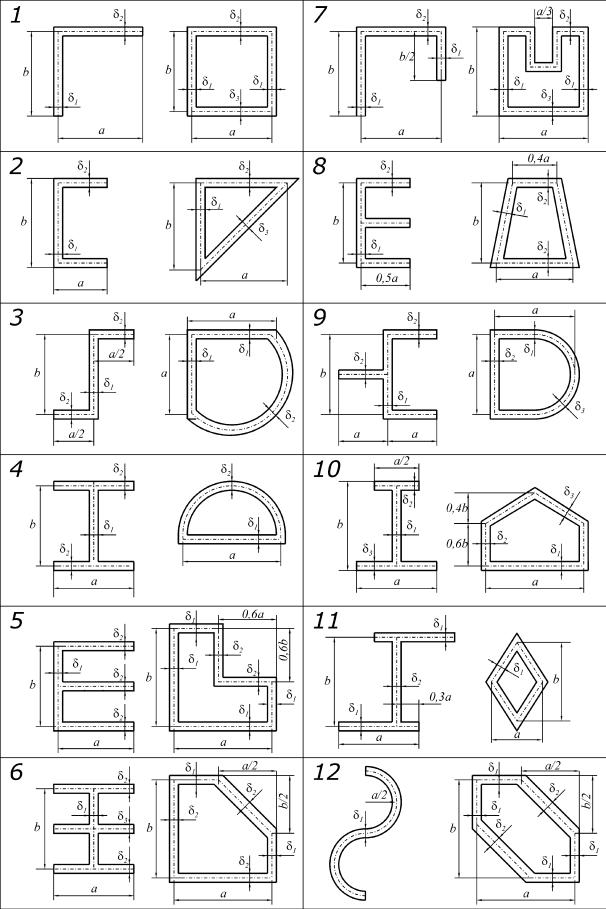
Рис. 3.35. Поперечные сечения тонкостенных стержней к задаче № 3 (сечения 1-12)
103
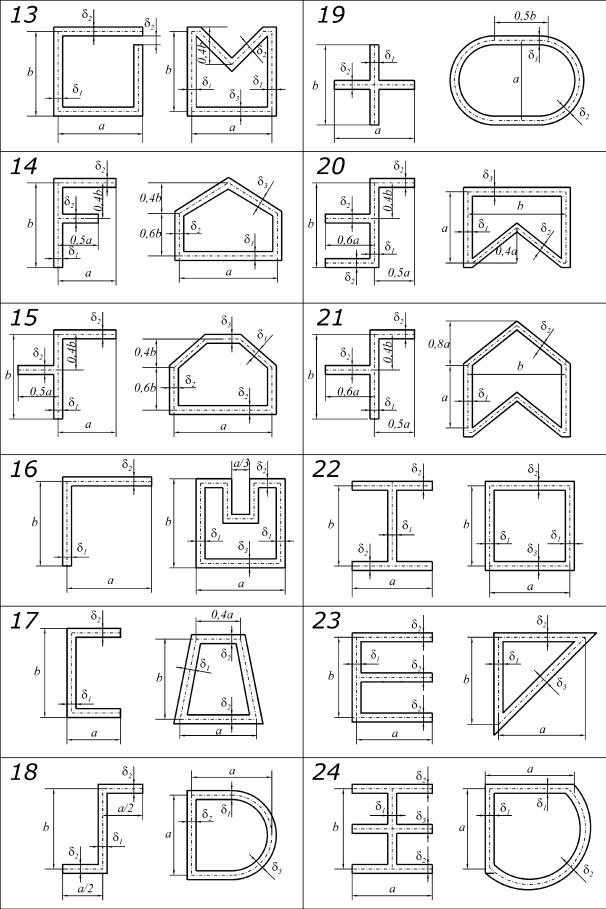
Рис. 3.36. Поперечные сечения тонкостенных стержней к задаче № 3 (сечения 13-24)
104
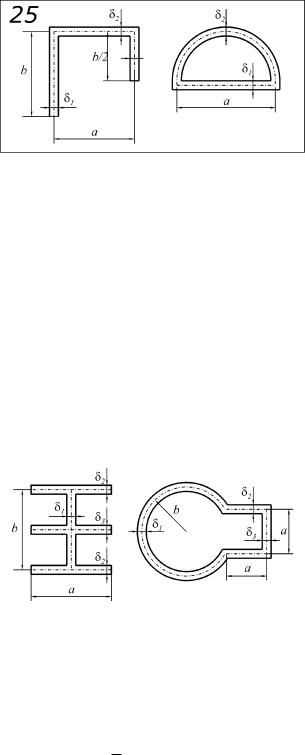
Рис. 3.37. Поперечные сечения тонкостенных стержней к задаче № 3 (сечение 25)
Пример решения задачи 3.
Рассмотрим следующий пример (рис. 3.38).
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3.7 |
|
|
|
Исходные данные к примеру решения задачи 3 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||
№ |
Крутящие |
Размеры стержня, |
Толщина элементов |
|
[ ], |
||||||||
моменты, кН м |
|
см |
|
стержня, мм |
|
|
|||||||
вар. |
|
|
|
|
МПа |
||||||||
M1 |
|
M2 |
a |
|
b |
1 |
|
2 |
|
3 |
|
||
|
|
|
|
|
|
|
|||||||
ХХХ |
0,2 |
|
4,0 |
10 |
|
20 |
5 |
|
6 |
|
7 |
|
80 |
а б
Рис. 3.38. Поперечные сечения тонкостенных стержней к примеру расчета
а– незамкнутого, б – замкнутого профиля
1.Определим момент инерции сечения тонкостенного стержня незамкнутого профиля по формуле Id 13 Li 3i . Заданное сечение состоит из семи
прямоугольников (рис. 3.43):
–прямоугольник 1 размерами 20 х 0,5 см,
–прямоугольники 2, 3 размерами 4,75 х 0,7 см,
–прямоугольники 4, 5, 6, 7 размерами 4,75 х 0,6 см.
105
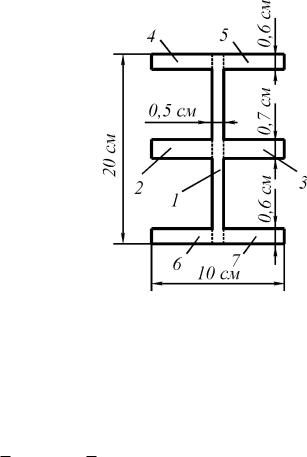
Рис. 3.39. Сечение тонкостенного стержня открытого профиля, представленное в виде прямоугольников
Данное сечение относится к типу «двутавр», поэтому = 1,2. Итак,
Id 13 Li 3i 1,2 13 20 0,53 2 4,75 0.73 4 4,75 0,63 3,95(см4).
2. Определяем крутящие моменты, действующие на каждый элемент стержня
- для прямоугольника 1
|
1 |
|
L |
|
|
|
|
1 |
20 0,53 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
M1 M кр |
3 1 1 |
|
400 |
3 |
|
|
84,4 |
(Н м); |
|||||||||
|
|
Id |
|
|
|
3,95 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
- для прямоугольников 2, 3 |
|
|
|
|
|||||||||||||
|
|
1 |
L |
|
|
1 |
4,75 0,73 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
M 2 M кр |
|
3 2 |
2 |
400 |
3 |
|
|
|
55,0 |
(Н м); |
|||||||
|
|
|
|
3,95 |
|
|
|||||||||||
|
|
|
|
Id |
|
|
|
|
|
|
|
|
|
|
|
|
|
- для прямоугольников 4, 5, 6, 7 |
|
|
|
|
|||||||||||||
|
|
1 |
L |
|
|
1 |
4,75 0,63 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
M 4 M кр |
|
3 4 |
4 |
400 |
3 |
|
|
|
34,6 |
(Н м). |
|||||||
|
|
|
|
3,95 |
|
|
|||||||||||
|
|
|
|
Id |
|
|
|
|
|
|
|
|
|
|
|
|
|
106
3. Определяем напряжения в стержне и выполняем проверку по условию прочности.
max |
|
M1 |
|
|
|
|
84,4 |
|
50,6 106 (Па) = 50,6 (МПа). |
|
|
|
|
|
|
|
|||
1 |
1 |
L 2 |
1 |
20 0,52 |
10 6 |
||||
|
|||||||||
|
|
3 |
|||||||
|
3 |
1 |
1 |
|
|
|
|
|
|
Условие прочности при кручении
max [ ].
50,6 80, т.е. условие прочности выполняется.
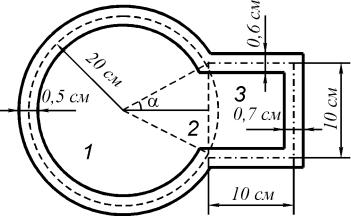
4. Для стержня замкнутого профиля определяем удвоенную площадь, охватываемую контуром сечения (рис. 3.44):
2(A1 A2 A3 ) .
Здесь
А1 = ( )R2 , |
A Rsin , |
A 10 10(см2). |
|
|||
|
|
|
2 |
3 |
|
|
sin |
10 |
/ 20 0,25 arcsin(0,25) 14,5 . |
|
|||
|
|
|||||
5 |
|
|
|
|
|
|
Имеем: |
|
|
|
|
|
|
|
|
|
|
2516 |
(см2). |
|
2 3,14 0,253 202 10sin14,5 100 |
||||||
|
|
|
|
|
|
|
Рис. 3.40. Определение величины
107
5. Определяем касательные напряжения в частях стержня и строим эпюру напряжений.
Напряжения в круговой части:
|
|
|
|
M |
z |
|
|
|
|
4 103 |
|
3,2 (МПа), |
||
|
1 |
2516 10 4 0,5 10 2 |
||||||||||||
1 |
|
|
|
|
||||||||||
напряжения в горизонтальных участках |
||||||||||||||
|
|
|
|
M |
z |
|
|
|
|
4 103 |
2,6 (МПа), |
|||
2 |
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
2516 10 4 0,6 10 2 |
|||||||||
|
|
|
|
|
|
|
|
|||||||
в вертикальной стенке |
|
|||||||||||||
|
|
|
|
M |
|
z |
|
|
|
|
4 103 |
2,3 (МПа). |
||
3 |
|
|
|
|
|
|
|
|
||||||
|
3 |
|
|
2516 10 4 0,7 10 2 |
||||||||||
|
|
|
|
|
|
|
||||||||
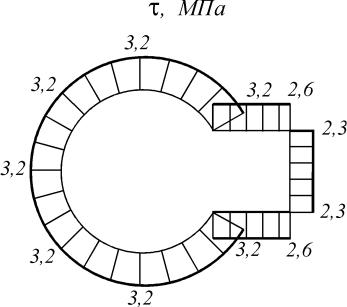
Эпюра напряжений представлена на рис. 3. 45.
Рис. 3.41. Эпюра касательных напряжений
6. Выполняем проверку условия прочности
max [ ];
3,2 80 .
Условие прочности выполняется.
108

РАЗДЕЛ 4
ИЗГИБ ПРЯМОГО БРУСА
1. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ И РАСЧЕТНЫЕ ФОРМУЛЫ
1. Основные понятия
Изгибом называется напряженно-деформированное состояние бруса, при котором в его поперечном сечении из шести внутренних силовых факторов два равны нулю - крутящий момент Мкр и продольная сила N.
Изгиб вызывается нагрузками, перпендикулярными к оси бруса, или сосредоточенными моментами, действующими в плоскости, в которой лежит его ось. Если все нагрузки, приложенные к брусу, лежат в одной плоскости, изгиб называется прямым.
Если в поперечном сечении действуют только изгибающий момент М, а поперечная сила Q равна нулю, изгиб называется чистым, если же в поперечном сечении Q ≠ 0, изгиб называется поперечным.
В данном разделе рассматривается нагружение бруса поперечными силами и парами сил, лежащими в одной, проходящей через ось бруса, плоскости, называемой силовой. Линия пересечения силовой плоскости с плоскостью поперечного сечения бруса называется силовой линией. Если силовая линия совпадает с главной центральной осью поперечного сечения, изогнутая ось бруса (его упругая линия) располагается в силовой плоскости. Такой вид изгиба назы-
вается плоским поперечным.
2. Балка. Опорные устройства (опоры) и опорные реак-
ции
Прямой брус, испытывающий изгиб, называется балкой. На расчетной схеме балку принято заменять ее осью (рис.4.1), при этом все нагрузки приводятся к этой оси. Часть балки (AB), расположенная между опорами, называется
еепролетом, а свешивающаяся ее часть (BC) - консолью.
Втеории изгиба употребляют
А |
В |
|
С |
термин волокно, уподобляя сплош- |
||
|
l |
|
lк |
|
|
ное вещество, из которого сделан |
|
|
|
|
брус, веществу волокнистой струк- |
||
|
|
|
|
|
|
туры, что, вообще говоря, непра- |
|
Рис.4.1. Расчетная схема балки |
вильно. Мы будем называть волок- |
||||
|
|
|
|
|
|
ном материальную линию, бывшую |
|
|
|
|
|
|
до деформации прямой, параллель- |
ной оси бруса. Координаты x и y |
точки пересечения волокна с плоскостью по- |
|||||
перечного сечения назовем координатами волокна. Еще раз подчеркнем, что понятие волокно для кристаллического материала условно.
109
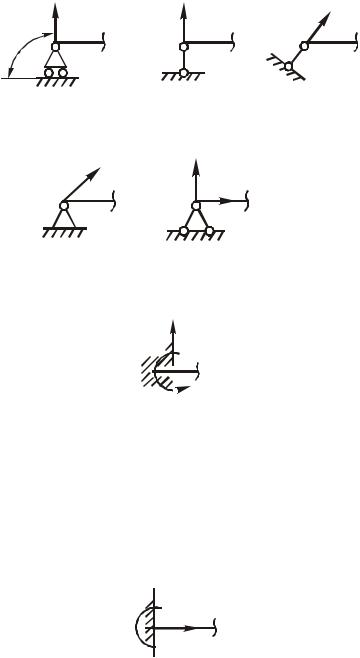
Для того чтобы балка могла воспринимать нагрузки и передавать их на основание или другие части конструкции, она должна иметь опорные устройства (опоры). Конструктивные формы опор весьма разнообразны. Чаще всего встречаются следующие основные типы опорных устройств:
|
|
|
|
|
|
а) шарнирно - подвижная |
90о |
V |
V |
R |
опора. Эта опора допускает по- |
||
|
ворот опорного сечения балки и |
|||||
|
|
|
|
|
|
его перемещение параллельно |
Рис.4.2. Схематическое изображение шар- |
|
опорной поверхности. Реакция |
||||
|
этой опоры проходит через шар- |
|||||
нирно – подвижных опор |
|
|||||
|
нир перпендикулярно опорной |
|||||
|
|
|
|
|
|
|
|
R |
|
V |
|
поверхности (рис.4.2); |
|
|
|
|
H |
|
б) шарнирно - неподвиж- |
|
|
|
|
|
|
|
ная опора допускает только по- |
|
|
|
|
|
|
ворот опорного сечения балки. |
|
|
|
|
|
|
Реакция R проходит через ось |
Рис.4.3. Схематическое изображение шарнир- |
шарнира, обычно ее представ- |
|||||
но – неподвижных опор |
|
|
|
|
ляют двумя составляющими - V |
|
|
V |
|
|
|
|
и H (рис.4.3); |
|
|
|
|
|
|
|
 M
M
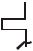
Рис.4.4. Схематическое изображение подвижной заделки
опорный момент M (рис.4.4);
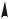 V
V
H
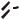
 M
M
Рис.4.5. Схематическое изображение неподвижной (жесткой) заделки
опорным моментом M (рис.4.5).
в) подвижная заделка
представляет собой паз, который допускает смещение опорного сечения параллельно опорным поверхностям. В опоре действуют два реактивных усилия: сила V, перпендикулярная опорной поверхности, и
г) заделка (жесткое за-
щемление) исключает угловое и линейные перемещения опорного сечения. Реакция заделки представляется ее тремя составляющими: силой V, перпендикулярной опорной поверхности, силой H, направленной вдоль оси балки, и
Опорные реакции определяются из уравнений равновесия балки (уравнений статики), число которых для плоской системы сил равно трем. Если их дос-
110
