
Расчетно-проектировочные работы и примеры их выполнения. Методическое пособие для студентов дневных / Основныезадачи 1-го семестра
.pdf
n
Sxi
yc i n1
Ai
i 1
y1A1 y2 A2 |
yn An , |
(2.17) |
|
A A |
A |
|
|
1 2 |
|
n |
|
где A1, A2 ,...An - площади составляющих фигур; x1, x2 , xn , y1, y2 ,... yn - ко-
ординаты их центров тяжести.
Примечание: При наличии двух осей прямой или косой симметрии центр тяжести сечения лежит на их пересечении.
Пример 2.5. Определить положение центра тяжести сечения, форма и размеры которого представлены на рис.2.9.
Разбиваем сечение на простые фигуры и YC 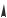 y0, y1 , y2 определяем их площади:
y0, y1 , y2 определяем их площади:
для прямоугольника:
|
a |
|
|
|
|
|
3a |
|
C2 |
x2 |
|
8a |
y=a |
|
|||
0 |
C1 |
x0 ,x1 |
|||
|
2 |
||||
|
C |
|
|
|
|
|
0,1a- |
2a |
C |
XC |
|
|
|
|
|||
|
|
|
|
||
|
y= |
|
|
|
|
|
C |
|
|
|
4a
Рис.2.9. К примеру 2.5.
A1 b1h1 4a 8a 32a2 ;
для равнобедренного треугольника:
A2 1 b2h2 2a 3a 3a2 . 2 2
Площадь сечения:
A A1 A2 32a2 3a2 29a2 .
Примечание: поскольку треугольник представляет собой отверстие, то перед значением его площади ставится знак «минус».
Вводим в сечении вспомогательную систему координат x0 , y0 , проводим центральные
оси фигур и определяем координаты их центров тяжести относительно осей x0 , y0 :
C1 |
x1 0, |
так как оси x0 , y0 совпадают с центральными осями |
|||||||
|
y |
|
0, |
||||||
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
прямоугольника; |
||
|
x2 |
0, |
|
|
|
||||
|
|
|
|
|
1 |
|
3a |
|
|
C2 |
y |
|
|
h |
a. |
||||
|
|
2 |
|
|
|||||
|
|
|
|
|
3 |
|
3 |
|
|
Координаты центра тяжести определяем по формулам (2.16 - 2.17). Заданное сечение симметрично относительно вертикальной оси, поэтому xC 0.
Ордината центра тяжести сечения равна:
51

yC y1 A1 Ay2 A2 0 32a2 2a 3a2 0,1a . 29a
Откладывая вниз по оси y0 отрезок 0,1a , обозначаем центр тяжести и проводим центральные оси сечения XC , YC . Эти оси являются также главными, поскольку ось YC совпадает с осью симметрии сечения.
При определении моментов инерции составной фигуры, включающей прокатные профили: равнобокие (рис. 2.10.а) и неравнобокие уголки (рис. 2.10.б), двутавры (рис. 2.10.в), швеллеры(рис. 2.10.г), геометрические характеристики приводятся в таблицах сортамента прокатной стали.
|
|
|
|
у |
|
у |
|
у |
у0 |
у |
х0 |
u |
|
х |
х |
х |
х |
|
|
х |
|
|||||
х |
|
х |
|
х |
|
|
|
|
|
|
|
|
|
|
|
||
х1 |
|
х1 |
х1 |
|
х1 |
у |
|
у |
х0 |
у |
у0 |
у |
|
u |
|
||
в) |
|
г) |
||||||
|
а) |
|
б) |
|
|
|||
Рис. 2.10. Стандартные прокатные профили
В таблицах сортамента имеются размеры профилей, координаты их центров тяжести и числовые значения моментов инерции относительно характерных координатных осей. Пользуясь сортаментом (см. приложение), следует обращать внимание на направление координатных осей, которые могут не совпадать для профиля в составе рассматриваемой фигуры и приведенного в сортаменте (в последнем случае данные берутся с учетом изменения направления осей).
Для уголкового профиля центральные оси, параллельные полкам, не являются главными центральными осями, и при вычислении главных центральных моментов инерции составной фигуры приходится вычислять центробежные моменты инерции относительно этих осей.
2.6.Изменение моментов инерции при повороте координатных осей. Главные оси и главные моменты инерции
Во всех случаях расчета брусьев на изгиб необходимо знать направление главных центральных осей инерции сечения и величину соответствующих (главных) моментов инерции. Поэтому в дополнение к изложенному необходимо ознакомиться с приемами отыскания главных осей несимметричного сечения.
52
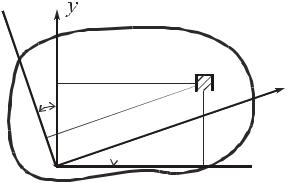
Возьмем сечение произвольной формы (рис. 2.11), отнесенное к произвольным осям х, у, и рассмотрим изменение моментов инерции при повороте осей.
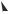
 1
1
O
x
x1
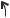
dA
 y1 x1
y1 x1
y
 x
x
Рис. 2.11. Соотношение между моментами инерции при повороте осей
Пусть нам известны осевые и центробежный моменты инерции сечения относительно выбранных осей х, у:
Ix y2dA; |
I y x2dA; |
Ixy xydA. |
(2.18) |
A |
A |
A |
|
Повернем обе оси на некоторый угол против часовой стрелки, условившись считать это направление поворота положительным, и определим мо-
менты инерции |
Ix |
, |
I y , |
Ix |
y , для новых осей x1 , y1 : |
|
||
|
1 |
1 |
1 |
1 |
|
|
|
|
|
|
Ix1 |
y12dA, |
I y1 x12dA, |
Ix1 y1 x1 y1dA . |
(2.19) |
||
|
|
|
A |
|
|
A |
A |
|
В повернутой системе осей координаты х1, у1 произвольной элементарной площадки сечения dA выразятся через прежние ее координаты следующим образом:
x1 |
x cos y sin , |
(2.20) |
|
|
|
y1 y cos x sin . |
|
|
Подставим эти значения координат в первое и последнее из равенств
(2.19):
Ix1 |
y12dA |
(ycos xsin )2 dA, |
|
|
|||||
|
|
A |
|
A |
|
|
|
|
(2.21) |
|
|
|
|
|
|
|
|||
1 |
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
||||
Ix |
y |
|
|
x1 y1dA |
|
|
(xcos ysin )(ycos xsin )dA. |
|
|
|
|
|
A |
|
|
A |
|
|
|
Раскрыв скобки под интегралами, получим после приведения:
53

Ix1 cos2 y2dA sin2 x2dA 2sin cos xydA, |
|
|
|||||
|
|
|
|
|
|
|
|
|
A |
|
A |
|
A |
|
(2.22) |
|
|
|
|
|
|
|
|
|
|
|
(cos2 sin2 ) xydA. |
|
|||
Ix1 y1 |
sin cos |
y2dA x2dA |
|
||||
|
|
|
A |
|
A |
|
|
|
A |
|
|
|
|||
Замечая, что интегралы правых частей равенств (2.19) являются моментами инерции относительно начальных осей х, у, перепишем эти равенства в следующем виде:
Ix |
|
Ix cos2 I y sin2 |
Ixy 2sin cos , |
|
(2.23) |
|||
1 |
|
|
Ix I y |
|
|
|
|
|
Ix |
y |
|
|
2sin cos Ixy (cos2 sin2 ). |
|
(2.24) |
||
1 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
Момент инерции I y |
найдем из (2.23), заменяя в нем на |
|
: |
|||||
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
||
I y |
|
Ix sin2 I y cos2 Ixy 2sin cos . |
|
(2.25) |
||||
1 |
|
|
|
|
|
|
|
|
Полученные формулы определяют все три момента инерции относи- |
||||||||
тельно повернутых осей. Складывая почленно (2.23) и (2.25), получим: |
|
|||||||
|
|
|
|
Ix I y Ix1 |
I y1 I p сonst, |
|
(2.26) |
|
т. е. сумма моментов инерции относительно любых взаимно перпендикулярных осей не изменяется при их повороте.
Далее удобно формулы (2.23)-(2.25) выразить через функции угла 2 , в результате чего будем иметь после приведения:
Ix |
|
I |
x |
I |
y |
I |
x |
I |
y |
|
|
|
|||
|
2 |
|
|
2 |
cos2 Ixy sin 2 , |
|
|||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Ix I y |
|
|
Ix I y |
|
|
||||||||
I y |
|
|
|
|
(2.27) |
||||||||||
|
|
2 |
|
|
|
|
2 |
|
cos2 Ixy sin 2 , |
||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ix |
y |
Ix |
I y |
sin 2 Ixy cos2 . |
|
|
|||||||||
|
|
2 |
|
|
|
|
|||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Примечание: Положительное направление отсчета угла - против хода часовой стрелки.
Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции принимают экстремальные значения, называются
главными.
54

Две взаимно перпендикулярные оси, из которых хотя бы одна совпадает с осью симметрии сечения, являются его главными осями. Главные оси, проходящие через центр тяжести сечения, называются главными центральными ося-
ми.
Поворачивая центральные оси, можно отыскать такое их положение, при котором центробежный момент инерции относительно этих осей будет равен нулю. Такие оси называются главными центральными. Угол 0 , на который
надо повернуть центральные оси xc , yc , чтобы они стали главными центральными, определяется по формуле
tg 2 0 |
|
2 |
|
Ix |
c |
y |
c . |
( 2.28) |
|
|
|
|
|||||
|
|
I y c |
Ix c |
|
||||
Осевые моменты инерции относительно этих осей называются главными центральными моментами инерции. Один из них имеет максимальную величину, другой - минимальную. Присвоим главным центральным осям индексы u , v , тогда главные центральные моменты инерции относительно осей u, v могут быть вычислены по формулам:
I |
u |
I |
xc |
cos2 |
0 |
I |
yc |
sin2 |
|
0 |
I |
xc yc |
sin 2 |
0 |
; |
||
|
|
|
|
|
|
|
|
|
|
(2.29) |
|||||||
|
|
I |
|
sin2 |
|
|
I |
|
|
cos2 |
|
|
I |
|
sin 2 |
|
|
I |
v |
xc |
0 |
y c |
0 |
x c yc |
0 |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
Эти же формулы могут быть записаны иначе, если использовать функции двойного угла:
Iu |
|
I x |
c |
I y |
c |
|
I x |
c |
I y |
c cos 2 0 |
I xc yc |
sin 2 0 ; |
|||
|
2 |
|
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.30) |
||
|
|
|
|
I y |
|
|
|
|
|
I y |
|
|
|||
Iv |
|
Ix |
c |
c |
|
Ix |
c |
c cos2 0 |
Ix c yc |
sin 2 0 . |
|||||
|
2 |
|
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для вычисления главных центральных моментов инерции, исключая тригонометрические функции угла 0 , можно получить следующую формулу:
I |
max |
|
Ixc I yc |
|
1 |
(I |
xc |
I |
yc |
)2 4I 2 |
. |
(2.31) |
|
|
2 |
|
2 |
|
|
xc yc |
|
|
|||
|
min |
|
|
|
|
|
|
|
|
|
Если главные центральные оси принять за исходные, то формулы перехода к произвольно выбранным центральным осям при повороте исходных осей принимают более простой вид
I x |
c |
Iu cos2 0 |
Iv sin2 0 |
|
Iu Iv |
Iu Iv cos2 0 ; |
|
|
|
|
|
2 |
2 |
|
|
I y |
Iu sin2 0 |
Iv cos2 0 |
Iu Iv Iu Iv cos 2 0 ; |
(2.32) |
|||
|
c |
|
|
|
2 |
2 |
|
|
|
|
|
|
|
||
55
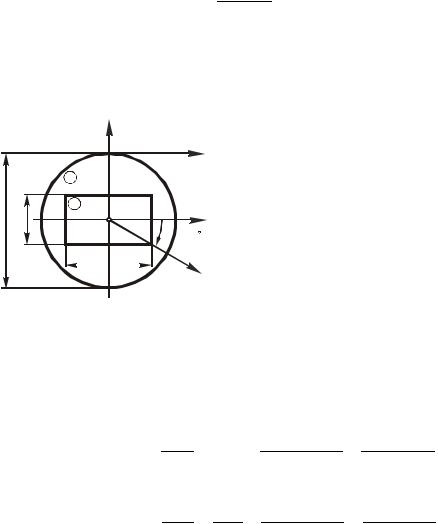
I |
x c yc |
Iu Iv sin2 |
0 |
. |
|
2 |
|
||
|
|
|
|
Пример 2.6. Определить моменты инерции сечения, представленного на рис. 2.12, относительно осей x , y и x1 , x2 .
|
|
|
y |
x1 |
|
|
|
|
|
|
|
1 |
|
|
6a |
2a |
2 |
x |
|
|
C |
30 x2 |
||
|
|
|
||
|
|
|
4 a |
|
|
|
|
|
|
Рис.2.12. К примеру 2.6
Разбиваем сечение на фигуры: 1- круг радиуса R 3a , 2- прямоугольник h 2a ,
b 4a . Вычисляем площадь сечения:
A A1 A2 R2 b h
3,14 (3a)2 4a 2a 20,26a2 .
Оси x , y являются главными централь-
ными, т. к. совпадают с осями симметрии сечения. Центробежный момент Ixy 0 .
Определяем моменты инерции относительно осей x , y
|
Ix |
Ix(1) |
Ix(2) |
|
R4 |
|
bh3 |
|
3,14 (3a)4 |
|
4a (2a)3 |
60,92a4 , |
|
|
4 |
12 |
4 |
12 |
|||||||||
|
|
|
|
|
|
|
|
|
|||||
|
I y |
I y(1) |
I y(2) |
|
R4 |
|
hb3 |
|
3,14 (3a)4 |
|
2a (4a)3 |
52,92a4 . |
|
|
4 |
12 |
4 |
12 |
|||||||||
|
|
|
|
|
|
|
|
|
|||||
|
Воспользовавшись формулами (2.10), вычисляем момент инерции |
||||||||||||
относительно оси x1 (расстояние между осями |
x и x1 определяем по чертежу |
||||||||||||
a 3a ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ix |
Ix |
a2 A 60,92a4 |
(3a)2 20,26a2 243,26a4 . |
|||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Момент инерции относительно оси x2 , |
повернутой на 30 отно- |
|||||||||||
сительно оси x , вычисляем по формуле (2.23), учитывая, что Ixy 0 |
|||||||||||||
Ix |
Ix cos2 I y sin2 |
60,92a4 cos2 ( 30) 52,92a4 sin2 ( 30) 58,92a4 . |
|||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2.7. Вычислить центробежный момент инерции неравнобокого уголка 100 63 8 мм относительно центральных осей x, y (рис. 2.13).
Для заданного уголка из таблицы сортамента выписываем его характеристики, необходимые для расчета:
Ix 127 см4 ; Iy 39,2 cм4 ; Iu = 23,4 cм4 ; tg = 0,391.
56

Центробежный момент инерции неравнобокого уголка 100 63 8 мм
u |
у |
|
относительно центральных осей x , y |
оп- |
||
|
|
|
ределяется по формуле |
|
tg |
|
|
|
v |
Ix,y (Ix I y |
2Iu ) |
|
|
|
|
tg 2 1 |
||||
|
|
|
|
|
|
|
х
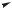
Рис.2.13.Неравнобокий уголок
100 63 8мм
= (127 39,2 2 23,4) |
0,3912 |
|
|
0,391 1 |
|
= 40,5 см4 .
Примечание: Поскольку большая часть площади уголка расположена во II и IV координатных четвертях, при подстановке значений в формулу ставится знак «-».
2.7. Радиусы инерции
Выражение момента инерции сечения относительно любой оси х на основании формулы среднего значения интеграла всегда можно представить в следующем виде:
Ix y2dA ix2 dA ix2 A, |
(2.33) |
|
A |
A |
|
где А – площадь сечения, а ix - ордината некоторой средней точки сечения.
Эта средняя ордината носит название радиуса инерции сечения относительно оси х и вычисляется по формуле
ix |
Ix . |
(2.34) |
|
A |
|
Аналогично радиус инерции относительно оси у
iy |
I y . |
(2.35) |
|
A |
|
Главным центральным осям XC и YC соответствуют главные центральные радиусы инерции
i |
|
|
|
I X |
C , |
i |
|
IY |
(2.36) |
X |
|
|
C |
||||||
|
|
|
A |
Y |
A |
|
|||
|
|
C |
|
|
C |
|
|||
|
|
|
|
|
|
|
|
||
Как следует из формул (2.34 – 2.36), размерность радиусов инерции
[м], [см].
57
РАЗДЕЛ 3
КРУЧЕНИЕ ПРЯМОГО БРУСА
3.1. Основные определения
Кручением называется такой вид деформации стержня, при котором в его поперечных сечениях из шести возможных силовых факторов действует только один – крутящий момент. Деформацию кручения испытывают валы двигателей и станков, оси локомотивов, элементы сложных пространственных конструкций.
Брус (стержень), работающий на кручение, называется валом. В технике чаще всего встречаются валы круглого поперечного сечения.
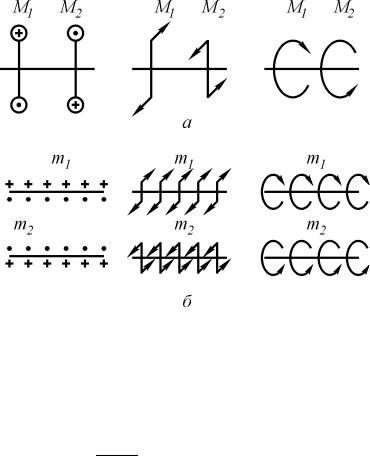
Крутящий момент, действующий в сечении вала, возникает из-за приложенных к валу сосредоточенных или распределенных крутящих моментов. Для изображения нагрузок, прикладываемых к валу, на расчетных схемах могут использоваться различные обозначения (рис. 3.1, а, б).
Рис. 3.1. Разные способы изображения сосредоточенных (а) и распределенных (б) крутящих моментов на расчетных схемах
В международной системе единиц измерения СИ крутящий момент измеряется в Н м (ньютон на метр), а интенсивность крутящего момента, распре-
деленного по длине вала – в Нмм (ньютон на метр на метр).
58
3.2. Определение крутящих моментов, действующих в поперечных сечениях вала. Построение эпюры крутящих моментов.
Крутящий момент, действующий в каком-либо сечении вала, можно определить с помощью метода сечений. Правило для определения крутящего момента можно сформулировать следующим образом: «Крутящий момент, действующий в сечении вала, равен алгебраической сумме крутящих моментов, действующих по одну сторону от сечения».
Знак крутящего момента определяется по его направлению относительно внешней нормали к рассматриваемому сечению. Общепринятого правила знаков для крутящих моментов нет.
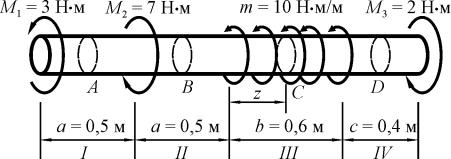
Пример 3.1. Построить эпюру крутящих моментов, действующих в поперечных сечениях вала, изображенного на рис. 3.2.
Рис. 3.2. Вал, нагруженный системой крутящих моментов
Рассмотрим вал, изображенный на рис. 3.3. Вал нагружен одним распределенным и тремя сосредоточенными моментами. Рассматриваемый вал находится в равновесии, в чем можно убедится, сложив приложенные к нему моменты.
M1 M 2 m c M 3 3 7 20 0,6 2 0
При расчете положительными считались моменты, закручивающие вал против часовой стрелки, момент, создаваемый распределенной нагрузкой определялся как произведение интенсивности m на длину участка c, на котором он действует.
Моменты, приложенные к валу, делят его на четыре участка. Определим, как меняются крутящие моменты по длине вала. Мысленно рассечем вал между точками приложения моментов M1 и M 2 . Части вала, расположенные слева и
справа от сечения находятся в равновесии. Рассмотрим часть вала, расположенную слева от сечения А (рис. 3.3.).
Крутящий момент M1, приложенный к отсеченной части слева от сечения, уравновешивается внутренним силовым фактором – крутящим моментом МА, действующем в сечении А. Другими словами, МА М1 3 (Н м). Крутящий
момент МА имеет знак «+», т.к. направлен против часовой стрелки при взгляде
59
на сечение А со стороны внешней нормали (то есть имеет положительное направление согласно принятому правилу знаков).
Рис. 3.3. Определение момента в сечении А
Крутящий момент МВ, действующий в сечении В (рис. 3.4.), уравновешивает крутящие моменты M1 и M 2 , направленные в противоположные стороны. Отсюда следует, что
M B M1 M 2 3 7 4 (Н м).
Рис. 3.4. Определение крутящего момента в сечении B
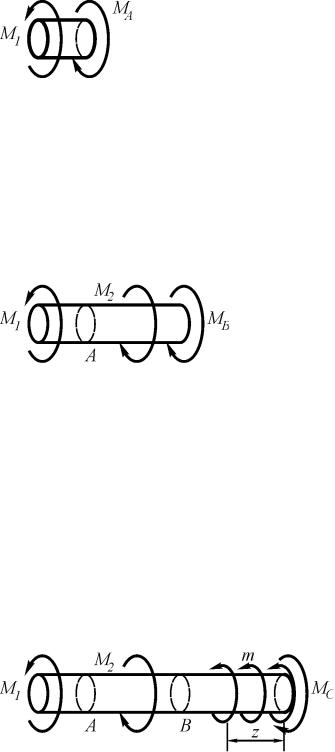
Крутящий момент в сечении С (рис. 3.5.) уравновешивает сосредоточенные моменты M1 , M 2 и момент интенсивностью m, распределенный по участ-
ку вала длиной z
M B M1 M 2 m z 4 10 z .
Таким образом, крутящий момент на третьем участке вала линейно зависит от координаты сечения z и изменяется от 4 Н м в начале участка (z 0 ) до 2 Н м в конце участка при z 0,6 м.
Рис. 3.5. Определение крутящего момента в сечении С
Крутящий момент M D в сечении D (рис. 3.6.) уравновешивает действие сосредоточенных моментов M1 , M 2 и момент интенсивностью m, распределенный по участку вала длиной 0,6 м, т.е.
60
