
Расчетно-проектировочные работы и примеры их выполнения. Методическое пособие для студентов дневных / Основныезадачи 1-го семестра
.pdf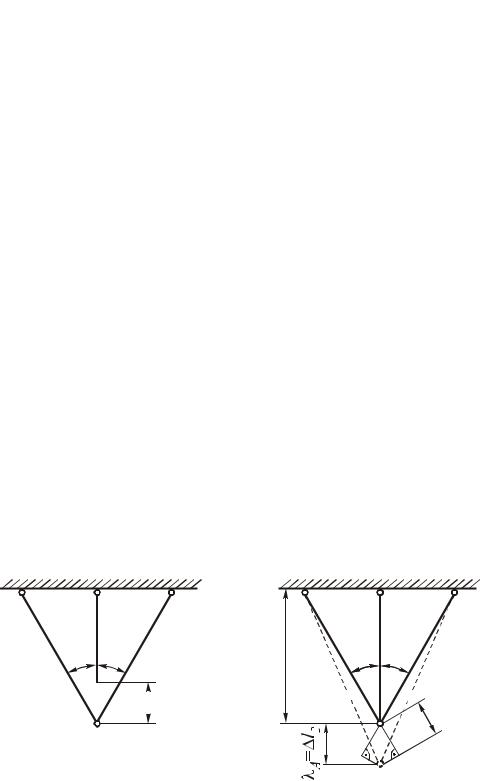
Отсюда и из уравнения статики
2 1 cos 2 |
0 . |
|
|
|
|
находим: |
|
|
|
|
|
1 |
cos2 |
E t t0 , |
2 2 cos3 |
E t t0 . |
|
|
1 2 cos3 |
|
1 2 cos3 |
|
|
При |
30 получим: |
|
|
|
|
1 39,2 МПа, 2 67,8 МПа. |
|
|
|||
При вычислениях принято |
1,2 10 5 C 1 , |
E 2 105 МПа. |
|||
Если бы нагревался один из боковых стержней, мы должны были бы рассмотреть более общий случай деформации, сопровождаемый горизонтальным смещением узла.
Как видно из решенного примера, температурные напряжения достигают довольно большой величины при сравнительно незначительных разностях температур. В стержневых системах температурные напряжения сами по себе не представляют опасности, так как наступающая пластичность ограничивает рост напряжений, а температурные деформации остаются во много раз меньше тех деформаций, при которых происходит разрушение (если речь не идет о весьма хрупких материалах). Однако наличие температурных напряжений может существенно повлиять на картину распределения усилий в системе.
Практическое осуществление статически неопределимых стержневых систем требует весьма точного изготовления стержней, чтобы при сборке концы их соединялись в узлах без применения усилия. В противном случае сборка становится возможной только за счет упругой деформации стержней и в системе возникают напряжения, называемые начальными или монтажными.
Предположим, например, что в предыдущем примере средний стержень сделан короче крайних на величину (рис. 1.29, 6). При решении вопроса о монтажных напряжениях будем предполагать, что усилия положительны и стержни удлиняются, хотя очевидно, что удлиняется только средний стержень, а крайние укорачиваются.
a) бa)
1 2 1

h
1 |
2 |
1 |
|
||
|
|
|
A |
|
|
|
l |
|
|
|
1 |
|
B |
|
|
|
|
|
||
|
|
|
|
||
|
|
|
A1 |
||
Рис. 1.29. Заданная система (а); диаграмма перемещений (б)
Уравнение совместности деформаций будет
41

l1 l2 cos .
Отсюда
l |
|
|
l |
2 |
|
1 1 |
|
2 |
|
cos . |
|
E |
|
E |
|
|
|
Уравнение равновесия:
2 1 cos 2 0 .
Полученная система уравнений весьма похожа на уравнения для температурных напряжений, только вместо l t t0 стоит . И
действительно, совершенно безразлично, сделать ли стержень короче или сделать его надлежащей длины, но потом укоротить путем охлаждения. Очевидный результат решения задачи следующий:
1 |
|
cos2 |
E |
, 2 |
|
2 cos3 |
E |
. |
|
2 cos3 |
l2 |
1 2 cos3 |
l2 |
||||||
|
1 |
|
|
|
1.8. Расчет бруса на жесткость при растяжении-сжатии
Элементы конструкций, испытывающие растяжение или сжатие должны удовлетворять не только условиям прочности, но и условию жесткости. Условие жесткости, которое можно записать в двух равноценных вариантах, имеет вид
max |
lmax |
[ ] |
или lmax [ l]. |
|
l |
|
|
В сопротивлении материалов условие жесткости применяется, как и рассмотренное выше условие прочности, при проведении трех видов расчетов: проектировочном расчете, при определении допускаемой условием жесткости нагрузки и при проверочном расчете. Чаще других проводится проверочный расчет.
Поверочный расчет на жесткость состоит в определении наибольших деформаций и сравнения их с допускаемыми величинами.
Пример 1.16. Стальной брус квадратного поперечного сечения, площадь которого равна 5 см2, растянут силой P = 40 кН. Проверить выполнение условия жесткости бруса.
Исходные данные для расчета: l= 1 м, Е = 2 1011 Па, [ l ] =1мм. Абсолютное удлинение бруса подсчитывается по формуле (1.9) и сравнивается с допускаемым
l |
N l |
|
40 103 1 |
0,4 10 3 м 0,4 мм 1мм; |
|
E A |
|
2 1011 5 10 4 |
|
l [l],
следовательно, условие жесткости выполняется.
42
РАЗДЕЛ 2
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ ФИГУР
1.Основные теоретические сведения и расчетные формулы
2.1.Основные определения.
Втеории растяжения-сжатия размеры и форма поперечного сечения бруса отражены в виде простейшей геометрической характеристики – площади сечения. В теорию изгиба и кручения, излагаемую в последующих разделах, входят более сложные геометрические характеристики сечения, называемые моментами инерции, к рассмотрению которых мы и переходим.
y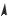
x dA
y
O |
x |
Рис. 2.1. Схема к определению моментов
Возьмем произвольную фигуру (сечение), отнесенную к координатным осям x и y (рис. 2.1).
Выражения
Sx ydA
A
(2.1)
Sy xdA
A
называются статическими моментами площади фигуры относительно осей x и y или моментами первой степени. Ин-
декс A внизу знака интеграла указывает, что интегрирование распространяется на всю площадь фигуры. На основании теоремы о моменте равнодействующей можно написать следующие равенства:
ydA Ayc , |
xdA Axc , |
(2.2) |
|||||
A |
|
|
|
A |
|
|
|
где A – площадь фигуры, xc , |
yc – координаты центров тяжести. |
|
|||||
Отсюда для определения координат центра тяжести получим такие |
|||||||
формулы: |
|
|
|
|
|
|
|
xc |
Sy |
, |
yc |
S |
x . |
(2.3) |
|
|
A |
|
|||||
|
|
|
|
A |
|
||
43
Если ось проходит через центр тяжести фигуры, то соответствующий статический момент, как легко видеть из формул (2.3), равен нулю.
Повышая под интегралом в выражениях (2.1) степень координат x , y
площадки dA, получим моменты площади второй, третьей и высших степеней относительно осей x , y .
Моменты площади второй степени
Ix y2dA, |
I y x2dA |
(2.4) |
A |
A |
|
называются осевыми (или экваториальными) моментами инерции относительно осей Ox , Oy .
Интеграл произведений элементарных площадок на обе координаты
Ixy xydA |
(2.5) |
A |
|
носит название центробежного момента инерции площади фигуры.
Если каждая элементарная площадка dA умножается на квадрат ее ра- диуса-вектора , проведенного из какой-либо определенной точки, например из начала координат, то интеграл называется полярным моментом инерции фигуры относительно выбранной точки (полюса)
|
|
I p 2dA . |
(2.6) |
|
|
|
A |
|
|
Полярный момент инерции всегда равен сумме осевых Ix и |
I y для лю- |
|||
бой пары взаимно |
перпендикулярных осей |
x и y , проходящих через полюс |
||
О (рис. 2.1). Для доказательства подставим значение 2 x2 y2 |
в формулу |
|||
(2.6): |
|
|
|
|
I p 2dA (x2 |
y2 )dA x2dA y2dA I y Ix . |
(2.7) |
||
A |
A |
A |
A |
|
Из выражений (2.4), (2.5) и (2.6) видно, что осевые и полярный моменты инерции – величины существенно положительные; центробежный момент инерции может быть и положительным и отрицательным и, в частности, равняться нулю, так как элементарные произведения xy для различных площадок
dA могут иметь разные знаки. Моменты инерции площадей – величины чисто геометрического характера, имеющие размерность (ед. длины)4; обычно их вы-
ражают в см4 . Оси x и y , проходящие через центр тяжести фигуры, называ-
ются центральными осями инерции фигуры.
44

2.2. Моменты инерции относительно параллельных осей
Пусть фигура произвольной формы отнесена к центральным осям x , y (рис. 2.2). Перейдем к параллельным осям x1 , y1 , проходящим на расстояниях a и b от предыдущих осей. Зависимость между координатами любой
y |
y |
элементарной площадки фигуры dA |
относительно новых и прежних осей |
||
1 |
a |
выразится так: |
|
x dA  y
y
O x b
x b
O1 |
x |
|
1 |
Рис.2.2. Схема к определению зависимости между моментами инерции для параллельных осей
x1 x a,
(2.8)
y1 y b .
Подставим эти значения x1 , y1
в общие выражения (2.4) и (2.5) моментов инерции относительно новых осей:
Ix1 |
y12dA (y b)2 dA y2dA 2b ydA b2 dA, |
|
||||||
|
A |
A |
|
|
A |
A |
A |
|
I y1 |
x12dA (x a)2 dA |
x2dA 2a xdA a2 dA, |
(2.9) |
|||||
|
A |
A |
|
|
A |
A |
A |
|
Ix1y1 x1 y1dA (x a)(y b)dA xydA a ydA b xdA ab dA. |
||||||||
A |
|
A |
|
|
A |
A |
A |
A |
Замечая, что |
xdA ydA 0 |
|
как статические моменты относительно |
|||||
|
|
A |
A |
|
|
|
|
|
центральных осей, |
dA A - площади всей фигуры, |
y2dA Ix , |
x2dA I y , |
|||||
|
|
A |
|
|
|
|
A |
A |
xydA Ixy , перепишем предыдущие равенства в следующем виде: |
|
|||||||
A |
|
|
|
|
|
|
|
|
|
|
Ix |
Ix b2 A, |
|
I y |
I y a2 A, |
(2.10) |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
Ix y |
Ixy abA. |
|
(2.11) |
||
|
|
|
1 |
1 |
|
|
|
|
Формулы (2.10) показывают, что при переходе от центральной оси к другой, ей параллельной, осевой момент инерции фигуры возрастает на величину, равную произведению площади фигуры на квадрат расстояния между
45
осями. Отсюда следует, что из всех параллельных между собой осей наименьшим моментом инерции обладает центральная ось, так как величины a2 A и
b2 A всегда положительны. Из формулы (2.11) видно, что при параллельном переносе обеих центральных осей центробежный момент инерции получает приращение (положительное или отрицательное), равное произведению площади сечения на координаты его центра тяжести в новой системе осей. Очевидно, что при переносе одной из центральных осей, т.е. когда a 0 или b 0 , центробежный момент инерции не изменится.
2.3. Понятие о главных осях инерции
Докажем, что для всякой плоской фигуры существует, по крайней мере, одна пара взаимно перпендикулярных осей с началом в данной точке, для которых центробежный момент инерции равен нулю. Такие оси называются глав-
ными осями инерции фигуры.
Выберем случайные взаимно перпендикулярные оси x и y , проходящие через произвольную точку О (рис. 2.1). Согласно определению центробежный момент инерции относительно этих осей Ixy xydA. Повернем те-
A
перь оси вокруг начала координат на 90 против часовой стрелки и обозначим их новые направления через x/ и y/ . При этом новые координаты любой эле-
ментарной площадки dA выражаем через прежние координаты следующим образом:
x/ y , |
y/ x , |
(2.12) |
а центробежный момент инерции относительно повернутых осей будет:
Ix/ y/ x/ y/ dA y( x)dA Ixy |
(2.13) |
|
A |
A |
|
Следовательно, при повороте осей на 90 центробежный момент инерции меняет знак на противоположный.
При постепенном повороте осей координаты элементарных площадок, а значит, и центробежный момент инерции изменяются непрерывно. Поэтому при некотором угле поворота, меньшем 90 , центробежный момент перейдет через нулевое значение, причем соответствующие по направлению оси и будут главными осями фигуры. В сопротивлении материалов почти всегда приходится иметь дело с центральными осями, почему главные центральные оси сечения обычно называют просто главными осями, подразумевая начало координат в центре тяжести сечения. Две плоскости, проходящие через продольную ось бруса и главные оси его поперечных сечений, называются главными плоско-
стями инерции бруса.
46

Любая ось симметрии фигуры является одной из главных центральных осей инерции. Пусть, например, сечение, показанное на рис. 2.3, симметрично относительно оси y . Тогда всякой элементарной площадке dA справа от оси y
соответствует такая же площадка слева с такими же по величине координатами, из которых одна x имеет противоположный знак.
|
y |
|
|
Все элементарные произведения |
|
|
|
|
|
xydA оказываются попарно равными и |
|
dA |
x<0 |
x>0 |
dA |
противоположными по знаку, отчего их |
|
интеграл, т.е. центробежный момент |
|||||
|
|
||||
y |
|
|
y |
инерции, обращается в нуль. Другая |
|
|
O |
|
x |
главная ось сечения будет, конечно, |
|
|
|
перпендикулярна к оси симметрии. Та- |
|||
|
|
|
|
ким образом, отыскание главных цен- |
|
|
|
|
|
тральных осей для фигур (сечений), |
|
|
|
|
|
имеющих хотя бы одну ось симметрии, |
|
|
|
|
|
не представляет никаких затруднений. |
Рис. 2.3. Схема к определению центробежного момента инерции симметричной фигуры
2.4. Моменты инерции простейших сечений
Пример 2.1. Вычислить моменты инерции прямоугольника относительно центральных осей, параллельных его сторонам (рис.2.4).
Выделим в сечении элементарную площадку dA в виде узкого прямоугольника, параллельного оси
x . Площадь элемента dA b dy .
Тогда момент инерции прямоуголь-
ника относительно оси x определя-
ем по формуле
h
Ix y2dA b 2 y2dy
A |
|
h |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
h |
|
|
|
h |
|
|
|
2 |
|
|
y3 |
2 |
|
h3b |
. |
2b y2dy 2b |
3 |
|
12 |
||||
0 |
|
|
0 |
|
|
||
Рис. 2.4. К примеру 2.1
Аналогично, если выделить элементарную вертикальную полоску шириной dx , получим: dA h dx и
47

|
b |
b |
|
b |
|
|
|
|
|
2 |
2 |
x3 |
2 |
|
b3h |
. |
|
I y x2dA h x2dx 2h x2dx 2h |
3 |
|
12 |
|||||
A |
|
b |
0 |
0 |
|
|
||
|
2 |
|
|
|
|
|
|
|
Пример 2.2. Определить момент инерции треугольника относительно оси x1 , проходящей через вершину параллельно основанию (рис.2.5).
Разобьем площадь треугольника на бесконечно тонкие полоски линиями, параллельными основанию. Площадь одной полоски вычислим как площадь прямоугольника с основанием a и высотой dy . Для полоски, находящей-
ся на расстоянии y от оси, a byh .
Площадь полоски
|
|
|
|
dA b ydy. |
|
|
|
|
h |
|
|
|
|
x1 |
|
y |
|
|
|
|
|
|
|
h |
h |
dy |
|
a |
2 3 |
|
|
|||
|
|
|
|
x |
|
|
|
|
h |
|
|
|
|
1 3 |
|
|
b |
|
x2 |
|
|
|
|
Рис.2.5. К примеру 2.2
Отсюда момент инерции
h |
3 |
Ix1 y2 |
bh ydy bh4 . |
o |
|
Для определения момента инерции относительно оси x2 , совпа-
дающей с основанием, мы должны сначала перейти к центральной оси x , а от нее – к оси x2 , применяя
дважды формулу (2.10):
I x |
I x |
2h 2 |
A |
bh3 |
2h |
|
2 bh |
|
bh3 |
, |
||||||
|
3 |
|
|
4 |
|
|
|
2 |
36 |
|||||||
|
1 |
|
|
|
|
3 |
|
|
|
|||||||
|
I x2 |
I x |
h |
2 |
|
bh3 |
|
h2 |
|
bh |
|
bh3 |
|
|
||
|
|
|
A |
36 |
|
9 |
|
2 |
|
12 |
. |
|
||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||
Пример 2.3. Вычислить |
|
полярный |
момент инерции круга относи- |
|||||||||||||
тельно его центра, а также момент |
|
инерции |
|
относительно центральной |
||||||||||||
оси. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
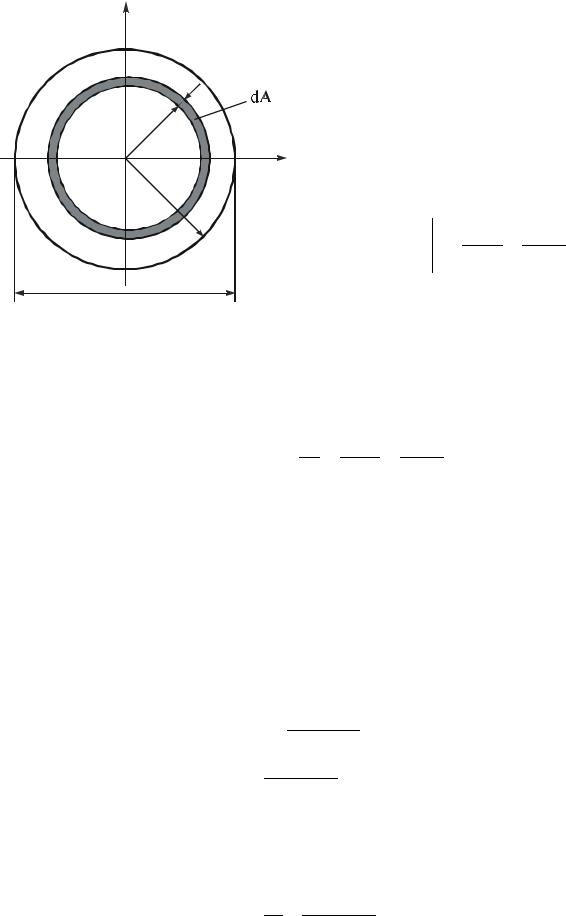
При вычислении полярного момента инерции выделим элементарную полоску в виде тонкого кольца толщиной d (рис. 2.6).
48
y |
Площадь такого элемента равна |
|
|
dA d 2 2 |
|
|
2 2 d d 2 2 2 d |
|
Ввиду малости слагаемым |
||
d |
||
|
d 2 пренебрегаем. |
|
Полярный момент инерции |
||
x |
||
|
r |
|
|
I p 2dA 2 3d |
r
d
|
A |
|
|
0 |
|
|
2 |
4 r |
|
r4 |
|
d |
4 |
4 0 |
2 |
32 |
. |
|||
|
|
|
|
Рис. 2.6. К примеру 2.3 |
|
|
|
|
|
|
|
|
В силу симметрии фигуры |
|
Ix I y . |
Используя свойство осевых и |
|||||
полярных моментов инерции I p Ix I y , |
получим: |
I p 2Ix . Отсюда |
||||||
Ix I y |
|
I p |
|
r4 |
|
d |
4 |
|
2 |
|
4 |
64 |
. |
||||
|
|
|
|
|
|
|||
Пример 2.4. Вычислить непосредственным интегрированием центробежный момент инерции треугольника (рис.2.7) относительно центральных осей, параллельных его сторонам.
Вычислим сначала центробежный момент инерции треугольника относительно осей x , y , совпадающих с его сторонами. Выделим элемент площади
dA by dy .
Из подобия соответствующих треугольников следует:
|
b |
y |
b (h y) |
, |
|
|
h |
|
|
|
|
|
|
|
следовательно, |
dA b (h y) dy . |
|||
|
|
|
h |
|
Абсцисса центра тяжести полоски
x by b (h y) . 2 2h
49
y |
y0 |
Тогда центробежный момент инерции треуголь- |
|
|
ника относительно осей x , y , равен |
h-y |
|
||
|
by |
dy |
|
h |
|||
|
|||
|
|
x0 |
|
y |
|
||
h 3 |
|
||
|
|
x |
|
b |
b |
3 |
Рис.2.7. К примеру 2.4
|
|
|
|
|
|
|
h b(h y) |
|
|
|
|
b(h y) |
|
|
|
|
|
|
|
||||||
Ixy |
xydA |
|
2h |
|
y |
|
|
|
h |
|
dy |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
A |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
2 |
h |
|
|
|
|
2 |
|
|
4 |
|
2h |
4 |
h |
4 |
b |
2 |
|
2 |
|||||
|
|
2 |
|
(h y)2 ydy |
b |
|
2 |
h |
|
|
|
|
|
|
h |
. |
|||||||||
2h |
|
|
|
2h |
|
|
2 |
|
3 |
|
4 |
|
|
24 |
|
||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Переходя к центральным осям x0 , |
y0 , получим: |
||||||||||||||||||||||||
Ix y Ixy a b A b2h2 |
|
bh |
b h b2h2 . |
|
|
||||||||||||||||||||
0 |
0 |
|
|
|
|
|
|
|
24 |
|
|
|
|
2 |
3 |
|
3 |
|
|
72 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2.5. Моменты инерции более сложных симметричных сечений
y
|
|
3 y |
y |
|
y |
4 |
||
|
|
|
|
|||||
|
|
|
|
|||||
|
|
3 |
|
4 |
|
|||
|
|
|
|
|||||
|
b4 |
2 |
|
|
|
С4 |
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
b3 |
2 |
|
|
|
|
С3 |
x3,4 |
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
1 |
b2 y |
|
|
С2 |
|
x2 |
a3,4 |
|
|
|
|
||||||
|
||||||||
|
||||||||
|
||||||||
|
|
|
|
|||||
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
a2 |
|
||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
b1 |
|
С1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
a1 |
|
|
|
x |
|||
|
|
|
|
|
|
|
|
|
O
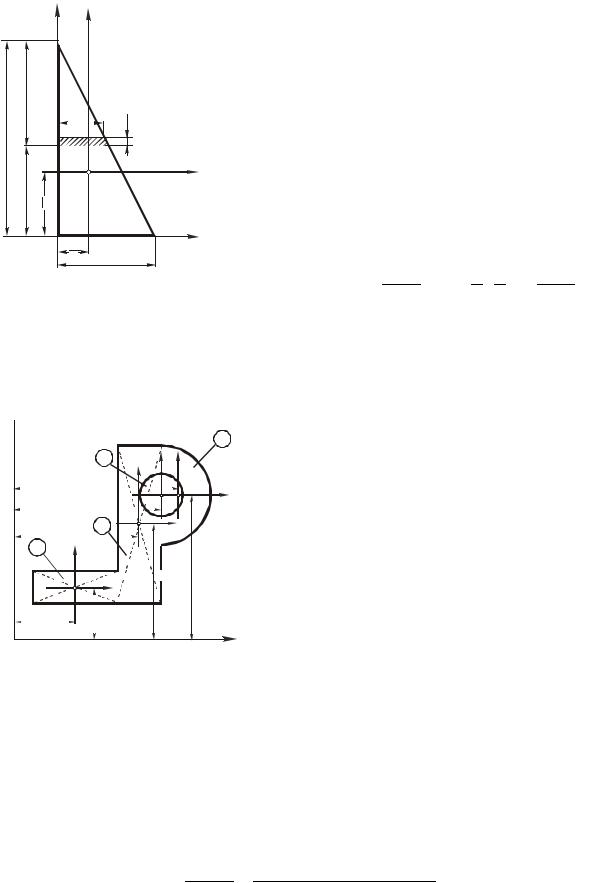
Рис. 2.8. Разбиение составных сечений на элементы
Если сложное сечение может быть разделено на отдельные части, имеющие форму прямоугольников, треугольников и т.п. (см. рис. 2.8), то момент инерции сечения можно найти как сумму моментов инерции отдельных его частей:
|
|
|
|
|
4 |
|
ai2 Ai ; |
|
Ix Ix(1) |
Ix(2) Ix(3) Ix(4) |
Ix |
||||||
|
|
|
|
|
i 1 |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.14) |
|
|
|
|
|
4 |
|
bi2 Ai ; |
|
I y I y(1) |
I y(2) |
I y(3) |
I y(4) |
|
I y |
|||
|
|
|
|
|
i 1 |
i |
|
|
|
|
|
|
|
Ixi yi |
aibi Ai |
||
|
|
|
|
|
4 |
|||
Ixy Ixy(1) |
Ixy(2) |
Ixy(3) |
Ixy(4) |
|
||||
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
(2.15) |
Предварительно определяется центр тяжести сложного сечения по следующим формулам:
n
Syi
xc i 1 n
Ai
i 1
x1A1 x2 A2 |
xn An ; |
(2.16) |
|
A A |
A |
|
|
1 2 |
|
n |
|
50
