
Расчетно-проектировочные работы и примеры их выполнения. Методическое пособие для студентов дневных / Основныезадачи 1-го семестра
.pdf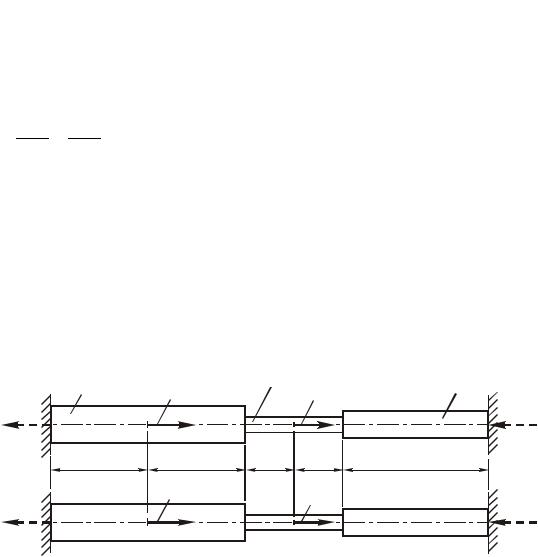
X XEA3a .
Сила Х должна быть такой, чтобы в результате действия сил Р и силы Х длина стержня не изменилась, поэтому
Р X 0 .
Отсюда
3EAPa 3EAXa 0 , X P .
Теперь легко подсчитать, что на первом участке усилие N1 P , на втором N2 0 и на третьем N3 P .
Пример 1.12. Для бруса, жестко заделанного обоими концами и нагруженного вдоль оси силами P1 и P2 , приложенными в его промежуточных сечениях (рис. 1.22, а), требуется построить эпюры продольных сил, нормальных напряжений и перемещений поперечных сечений. Проверить прочность бруса, если материал – сталь Ст 4 ( Т 260МПа); требуемый
коэффициент запаса [nт] = 1,6.
а) |
3A |
P1=2P |
A=3см2 |
2A |
|
RA |
|
P2=P=60кН |
|||
|
|
|
|
RB |
|
A |
|
|
|
|
B |
|
2а |
2а |
а |
а |
3а |
б) |
|
2P |
|
P |
RB=X |
A |
|
|
|
|
|
RA |
|
|
|
|
B |
Рис. 1.22. Расчетная схема бруса (а); статически определимый брус, нагруженный заданными силами и реакцией Х (б)
Решение. В заделках бруса возникают реакции, направленные вдоль его оси. Имеем систему сил, направленных по одной прямой, для которой статика
дает одно уравнение равновесия: |
|
Z 0 ; RA P1 P2 RB 0. |
(1.20) |
Неизвестных реактивных сил две, следовательно, система один раз статически неопределима.
Для составления уравнения перемещений отбросим одну из заделок, например правую, и заменим ее действие на брус соответствующей реактивной силой RB (рис. 1.22, б). Получим статически определимый брус, нагруженный кроме заданных сил P1 и P2 неизвестной реактивной силой RB X . Этот
статически определимый брус нагружен так же, как заданный статически неопределимый, т.е. эквивалентен ему. Эквивалентность этих двух брусьев позволяет утверждать, что второй брус деформируется так же, как первый, т.е. перемещение В сечения В равно нулю:
31
B 0 .
Применив принцип независимости действия сил, перепишем это уравнение в виде
B BР |
BР |
BX |
0 , |
(1.21) |
1 |
2 |
|
|
|
т.е. перемещение от совместного действия всех сил равно алгебраической сумме перемещений от действия каждой силы в отдельности.
В обозначениях перемещений первая буква индекса указывает о перемещении какого сечения идет речь; вторая – причину, вызывающую это перемещение (сила P1 и т.д.).
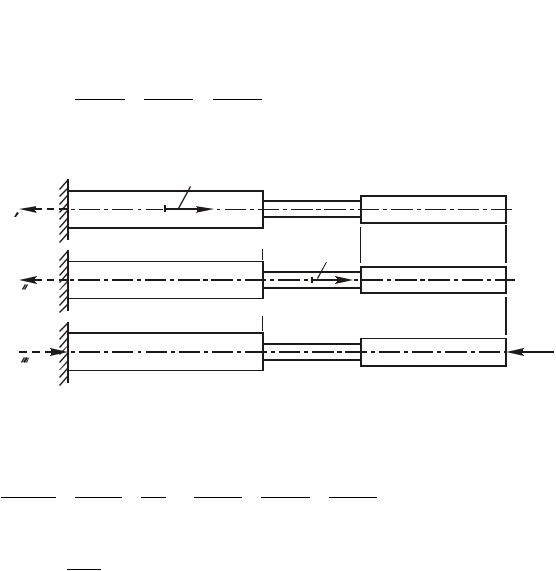
На рис. 1.23 показаны схемы нагружения бруса каждой из сил в отдельности, там же показаны соответствующие реакции левой заделки.
Пользуясь этими схемами, определим перемещения:
BР |
|
2P 2a |
равно удлинению участка АС; |
|
|||||||||||||
1 |
|
E 3A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BР |
P 4a Pa равно сумме удлинений участков AD и DE. |
||||||||||||||||
2 |
|
E 3A |
Ea |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
BX |
|
X 4a |
|
X |
2a |
|
X 3a |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
равно сумме укорочений участков AD, |
||||||||||
|
|
E 3A |
|
EA |
|
|
E 2A |
|
|
|
|
|
|||||
DK, KB. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2P |
|
|
|
|
|
|
|
|
|
RA =2P |
|
A |
|
С |
|
|
|
|
|
D |
|
|
|
|
B |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
RA =P |
|
A |
|
|
|
|
|
|
|
D |
|
Е |
|
B |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
RA =Х |
|
A |
|
|
|
|
|
|
|
D |
|
|
|
К |
B |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Рис. 1.23. Схемы нагружения бруса каждой из сил в отдельности |
|||||||||||||||||
Подставляя значения BР |
, BР |
и BX |
в уравнение (1.21), имеем |
||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
2P 2a |
|
P 4a |
|
Pa |
|
|
X |
4a |
|
X 2a |
|
X 3a |
0 , |
||||
E 3A |
E 3A |
EA |
|
|
3A |
|
EA |
|
|
||||||||
|
|
|
E |
|
|
|
|
E 2A |
|
||||||||
откуда X 2229P .
Статическая неопределимость раскрыта – имеем статически определимый брус, заделанный одним концом, нагруженный известными силами P1, P2 и
32
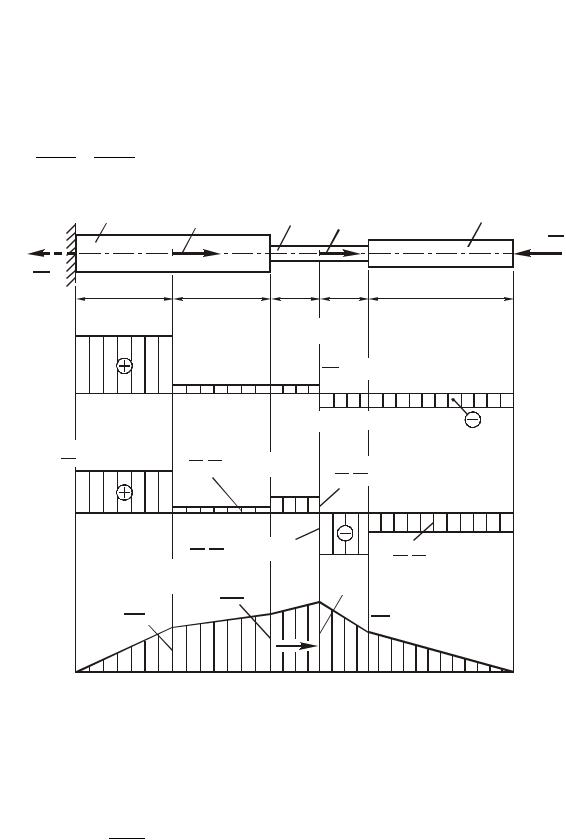
X 2229Р (рис. 1.24, а). Эпюры продольных сил и нормальных напряжений
строят обычным путем, как для любого статически определимого бруса. Эти эпюры даны на рис. 1.24, б, в.
Наибольшие по абсолютному значению напряжения возникают в поперечных сечениях участка EK – это опасные сечения.
Проверка прочности:
n |
Т |
|
260 1,72 n |
. |
|
|
|
|
|
||
Т |
max |
|
151,6 |
|
Т |
|
|
|
|
|
|
|
а) |
|
3A |
|
P1=2P |
A |
P2=P |
|
2A |
||
|
|
|
|
|
|
|
|
|
|
|
X= 22P |
|
|
|
|
|
|
|
|
|
|
|
29 |
RA = 2965P |
A 2а |
C 2а D |
а |
Е |
K |
3а |
B |
||||
|
|
а |
|
|
|||||||
|
|
|
|
65 |
|
Эпюра N |
|
|
|
||
|
|
|
|
29 P=134,5кН |
|
7 |
|
|
|
||
|
б) |
|
|
|
|
|
|
29 P=14,5кН |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эпюра |
22 |
|
|
|
|
|
|
|
|
|
|
29 P=45,5кН |
|
|
||||
|
65 P |
=149,4 МПа |
|
7 P |
=16,1 МПа |
7 P |
|
|
|
||
|
87 А |
|
87 А |
=48,2 МПа |
|
||||||
|
|
|
|
|
|
|
|
29 А |
|
||
|
в) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 P |
=151,6 МПа |
|
|
11 P =75,8 МПа |
||
|
|
|
|
|
29 А |
|
|
||||
|
|
|
Эпюра |
|
|
|
165 F |
|
29 А |
|
|
|
|
|
144 |
|
|
|
|
||||
|
|
|
|
|
|
87 |
|
|
|
||
|
|
|
130 P |
|
|
87 P |
|
|
99 |
P |
|
|
|
|
87 |
|
|
|
|
|
87 |
|
|
г)
Рис. 1.24. Статически определимый брус, нагруженный известными силами и реакцией (а); эпюра продольных сил (б); эпюра нормальных напряжений (в); эпюра перемещений (г)
Построение эпюры перемещений ничем не отличается от изложенного в примере 1.4. Эта эпюра дана на рис. 1.24, г; для сокращения записей введено
обозначение EAa . Построение эпюры начинаем от левого защемленного
конца бруса:
A 0 ;
33
|
|
65 |
|
|
|
|
|
|
|
|
|
|
|
29 |
P 2a |
130 |
|
|
|
|
|
||
С lAC |
|
|
|
|
P ; |
|
|
|
|||
|
E 3A |
87 |
|
|
|
||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
130 |
|
7 |
|
P 2a |
|
144 |
|
D C lCD |
P |
29 |
|
|
P . |
||||||
|
|
|
|
87 |
|
E 3A |
|
87 |
|
||
На правом конце бруса, в сечении В, ордината эпюры равна нулю, так как в заданном брусе это сечение жестко закреплено, именно из этого условия определено значение Х.
Кратко остановимся на решении одной из задач, аналогичных рассмотренной. Предположим, что до нагружения бруса между его правым торцом и заделкой имеется малый зазор (рис. 1.25, а). Масштаб, в котором на чертеже дана величина зазора, во много раз больше, чем масштаб отрезков a, 2a и т.д. Если при нагружении бруса зазор не закрывается, то система статически определима. Если удлинение бруса (в предположении, что он может деформироваться свободно, т.е. правая заделка вообще отсутствует) больше зазора, то между правым торцом бруса и заделкой возникает сила взаимодействия, определить которую с помощью одних лишь уравнений статики нельзя – задача будет статически неопределимой. Отличие ее от предыдущей состоит в том, что суммарное (от заданных сил и правой опорной реакции) перемещение правого торца бруса следует приравнять не нулю, а зазору: B .
Примем для определенности, что 2Pa 2 P Перемещение сечения |
В |
|||||
|
|
|
|
|
EA |
|
от действия сил P1 |
и P2 (в предположении, что правая заделка отсутствует), как |
|||||
было найдено выше, |
|
|
|
|
||
BР |
BР BР 11 Pa |
11 |
P , |
|
||
|
1 |
2 |
3 EA |
3 |
|
|
|
|
|
|
|
||
т.е. BF и, следовательно, система статически неопределима. Составим и |
||||||
решим |
уравнение |
перемещений, |
рассматривая брус, изображенный |
на |
||
рис. 1.25, б:
B BР1 BР2 BX
или
113 F 296 X 2 P
(определение ВХ см. выше), отсюда X 1029P .
Построение эпюр N, , выполняется так же, как и в случае отсутствия зазора; указанные эпюры даны на рис. 1.25, в, г, д.
Очевидно, на правом конце бруса ордината эпюры равна начальному зазору .
34
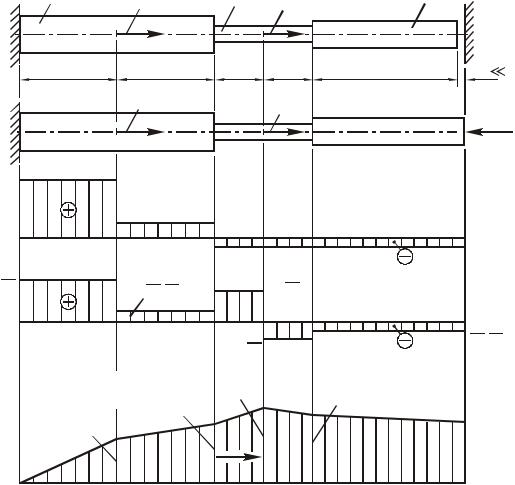
а) |
3A |
|
P1=2P |
A |
P2=P |
|
2A |
|
A |
|
|
|
|
|
|
|
B |
|
2а |
|
2а |
|
а |
а |
3а |
а |
б) |
|
|
P1 |
|
|
P2 |
|
X= 2910P |
|
|
|
|
|
|
|||
|
|
2977P |
|
2919P |
|
Эпюра N |
|
|
в) |
|
|
|
|
|
|
|
|
77 P |
|
|
|
|
|
19 P |
|
2910P |
|
|
19 P |
|
|
Эпюра |
|
||
87 А |
|
|
87 А |
|
|
29 А |
|
|
г) |
|
|
|
|
|
|||
|
|
|
|
|
|
|
5 P |
|
|
|
|
|
|
10 F |
|
|
|
|
|
|
|
|
|
|
29 А |
|
|
|
|
|
|
29 А |
|
|
|
|
|
|
|
|
|
|
|
|
|
Эпюра |
|
|
249 |
|
219 |
|
|
|
192 |
P |
87 P |
|
87 P |
|
||
|
154 |
P |
87 |
|
|
|
2 P |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||
|
87 |
|
|
|
|
|
|
|
д)
Рис. 1.25. Статически определимая система (а); статически неопределимая система (б); эпюра продольных сил (в); эпюра нормальных напряжений (г); эпюра перемещений (д)
Пример 1.13. Весьма жесткая балка подвешена на трех стальных стержнях одинакового сечения А = 4 см2 и нагружена силой P, как показано на схеме (рис. 1.26, а). Определить допускаемое значение силы P, если для материала стержней [ ] = 160 МПа.
Решение.
Определяем степень статической неопределимости.
Система один раз статически неопределима, так как неизвестных сил три, а статика дает два уравнения равновесия (плоская система параллельных сил).
Рассекаем стержни и составляем уравнения равновесия сил, действующих на балку (рис. 1.26, б):
Y 0 ; |
N1 N2 N3 P 0 ; |
|
M A 0; |
N2a P3a N3 4a 0 |
(1.22) |
или |
|
|
N2 4N3 |
3P . |
(1.23) |
35
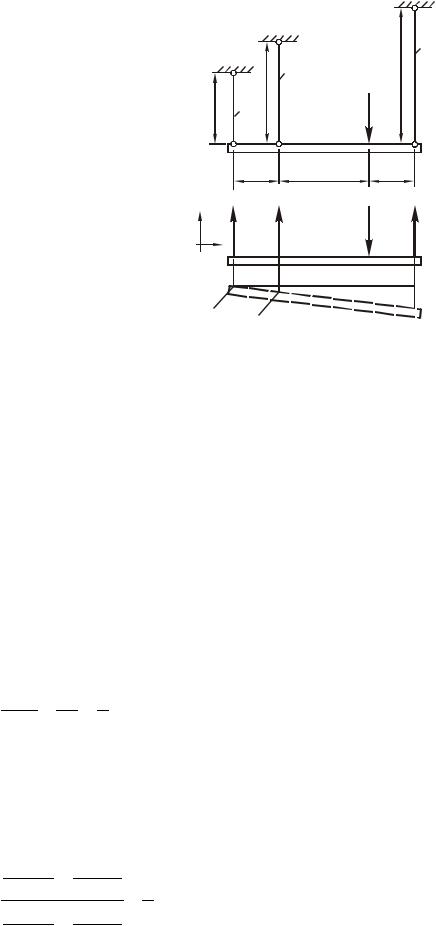
а)
|
|
|
|
3 |
|
3l |
2 |
|
4l |
2l |
|
|
P |
|
|
1 |
|
|
|
|
A |
B |
С |
D |
|
а |
|
2а |
а |
б) |
N1 |
N2 |
|
P N3 |
у |
|
|||
х |
A |
B |
С |
D |
ЕК
A1 |
D1 |
|
B1 |
||
|
Рис. 1.26. Расчетная схема балки (а); равновесие сил, действующих на балку (б)
Покажем деформации стержней. Мы предположили, что все стержни растянуты. Если в результате решения получим ответ для силы в каком-либо стержне со знаком минус, это укажет, что предположение было неверно и фактически этот стержень сжат.
В силу жесткости балки изгибом ее можно пренебречь. В результате деформации стержней балка несколько опустится и наклонится, оставаясь прямолинейной. Примерное положение балки после деформации стержней показано на рис. 1.26, б штриховыми линиями (конечно, удлинения стержней показаны сильно преувеличенными).
Очевидно, AA1 l1 ; BB1 l2 ; DD1 l3 .
Проведя вспомогательную прямую А1K, параллельную первоначальному
положению балки, из рассмотрения подобных треугольников A1EB1 и A1KD1 |
||||
получим |
|
|
|
|
B1E |
a |
|
|
1 |
D K |
4a |
|
4 |
|
1 |
|
|
|
|
или |
|
|
|
|
l2 l1 |
|
1 . |
||
l |
l |
|
|
4 |
3 |
1 |
|
|
|
Выражая удлинения стержней по формуле Гука, получаем уравнение перемещений в виде
N2 3l |
|
N1 2l |
|
1 |
|
||
|
EA |
|
EA |
|
, |
||
N |
3 |
4l |
|
N 2l |
|
4 |
|
|
|
1 |
|
|
|
||
|
EA |
|
EA |
|
|
|
|
откуда
36
6N2 3N1 2N3 . |
(1.24) |
Решая совместно уравнений (1.22), (1.23) и (1.24), выражаем силы в стержнях через искомую силу Р:
N1 |
2 |
Р; N2 |
9 |
Р; N3 |
|
24 |
Р. |
|
35 |
|
35 |
|
|
35 |
|
Наибольшая продольная сила, а, следовательно, и напряжение возникают в стержне 3. Составляя для него условие прочности, определяем допускаемое значение силы Р:
D |
N |
3 |
|
|
24 |
P |
, |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
A |
|
|
35 |
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
35 |
|
|
|
35 |
|
|
|
10 |
4 |
160 10 |
6 |
93,3 |
10 |
3 |
H 93,3 |
кН. |
|||||
|
|
|
A |
|
4 |
|
|
|
|||||||||||||||
|
24 |
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
При этом стержни 1 и 2 будут недогружены: |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N1 |
|
|
93,3 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
A |
|
|
35 |
|
|
|
|
13,3 10 |
6 |
Па = 13,3 МПа; |
|
||||||||||||
|
|
A |
|
4 10 4 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
9 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N2 |
|
|
93,3 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
B |
|
|
|
35 |
|
|
|
|
60 |
10 |
6 |
|
Па = 60 МПа. |
|
|
|
|||||||
|
|
A |
|
4 10 4 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 1.14. Система из трех шарнирно соединенных стальных стержней нагружена, как показано на схеме (рис. 1.27, а). Определить из расчета на
прочность требуемые площади стержней, если A1 A2 A ; |
A3 2A и |
140 МПа. |
|
a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
||
|
|
|||||
|
|
|
|
|
||
|
|
P=100 кН |
|
o |
||
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
l |
|
|
1 |
A1 |
B |
|
|
h |
|
|
3 |
б)
y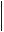
P
N1
 N2
N2
A |
x |
|
|
|
N3 |
Рис. 1.27. Расчетная схема системы (а); равновесие узла А (б)
37

Решение. Система один раз статически неопределима: статика дает для плоской системы сходящихся сил два уравнения равновесия, а неизвестных сил в стержнях три.
Вырезаем узел А (рис. 1.27, б) и составляем уравнения равновесия действующих на него сил. Предполагаем, что стержни 1 и 2 растянуты (силы N1 и N2 направлены от узла), а стержень 3 сжат (сила N3 направлена к узлу):
X 0; N1 sin N2 sin 0 |
(1.25) |
и |
|
Y 0 ; N1 cos P N2 cos N3 0 |
(1.26) |
или, учитывая (1.25), |
|
2N1 cos N3 P . |
(1.27) |
Зависимость между изменениями длин стержней получаем из диаграммы перемещений, показанной на рис. 1.27, а: на продолжении стержня 1 откладываем произвольный отрезок, соответствующий l1 и опускаем из его
конца перпендикуляр на направление стержня 3. Получаем точку А1 , дающую положение шарнира А после деформации. Очевидно, перемещение шарнира A A равно укорочению стержня 3 l3 . Из прямоугольного треугольника
ABA1 имеем
l3 l1 cos
и
N3l3 |
|
|
|
N1l1 |
|
|
|
||
|
|
|
EA |
|
|
|
|||
EA |
|
|
|
cos |
|
|
|
||
3 |
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N1h |
|
|
|
N3h |
|
|
|
cos |
|
, |
|
||
E 2A |
|
|
|
EAcos |
|
|
|||
откуда |
|
|
|
|
|
|
|
|
|
N3 |
|
2N1 . |
|
|
(1.28) |
||||
|
cos2 |
|
|
|
|||||
Решая совместно (1.27) и (1.28), получаем |
|||||||||
N1 N |
2 |
Pcos2 |
|
||||||
2 1 cos3 ; |
|
||||||||
N3 |
|
|
|
|
P |
|
|
|
|
1 cos3 . |
|
|
|||||||
Напряжения в стержнях: |
|
||||||||
|
|
|
|
N |
|
Pcos2 |
; |
||
2 |
1 |
2A1 cos3 |
|||||||
1 |
|
|
|
A |
|
||||
|
|
|
|
|
|
|
|||
38

3 |
N3 |
|
P |
|
. |
|
2A |
|
2A1 cos3 |
|
Очевидно, напряжения в стержне 3 больше, чем в стержнях 1 и 2, поэтому требуемую площадь сечения определяем из условия прочности стержня 3:
|
|
P |
|
, |
|
|
3 |
2A1 cos3 |
|
|
|
||
откуда |
|
|
|
|
|
|
|
|
P |
|
100 103 |
4 м2 = 216 мм2; |
|
A 2 1 cos3 |
|
2 140 106 1 cos3 30 2,16 10 |
||||
A A |
A 216 мм2; A 2A 432 мм2. |
|
|
|||
1 |
2 |
|
|
3 |
|
|
Стержни 1 и 2 недогружены: |
|
|
||||
|
|
Pcos2 |
100 103 cos2 30 |
|
106 Па = 105 МПа. |
|
1 |
2 |
2A1 cos3 2 216 10 6 1 cos3 30 105 |
||||
Однако, отсюда нельзя делать вывод о возможности уменьшения их сечений, так как силы в стержнях найдены при вполне определенном соотношении их жесткостей, указанном в условиях задачи. Если уменьшить сечения боковых стержней, то и силы в них уменьшатся, а в среднем стержне сила возрастет. В рассмотренном примере отражена существенная особенность проектного расчета статически неопределимых систем – необходимость соблюдения заранее заданного (или выбранного) соотношения жесткостей элементов. Как известно, в статически определимых системах можно выбирать сечение каждого стержня совершенно независимо от сечений остальных стержней системы.
1.7. Температурные и монтажные напряжения
Изменение температуры стержней статически неопределимых систем вызывает температурные деформации, которые, как правило, не удовлетворяют условиям совместности деформаций. Поэтому в стержнях возникают упругие напряжения и соответствующие им упругие деформации. Общие деформации, состоящие из температурных и упругих, должны удовлетворять уравнениям совместности деформации. Рассмотрим простейший пример, когда стержень помещен при температуре t0 между неподвижными стенками, после чего температура его повышается до t. Условие совместности деформации заключается в том, что l 0 .
Температурная часть удлинения:
tl t t0 l ,
здесь - коэффициент линейного температурного расширения материала. Упругая часть:
0l El .
Таким образом:
39
l t t0 l l 0.
E
Отсюда
E t t0 .
Схема решения более сложных статически неопределенных задач о температурных напряжениях ничем не отличается от общей схемы, данной в предыдущем параграфе, только в пункте 2 схемы вместо закона Гука следует пользоваться формулой
li ili ti |
Pili . |
|
Ei Ai |
Пример 1.15. В системе, изображенной на рис. 1.28 и собранной при температуре t0 20 , средний стержень нагрет до t 70 , температура
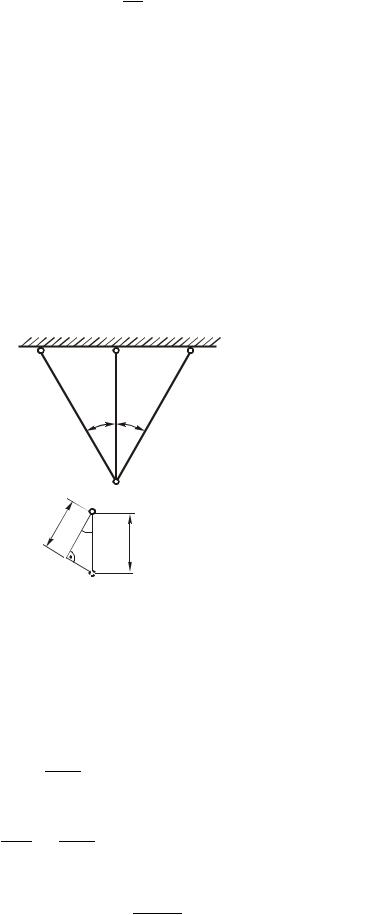
крайних осталась без изменения. Площади сечения стержней одинаковы, материал – сталь. Требуется найти напряжения.
a)
1 2 1
б)
|
l |
|
1
2l
Рис.1.28. Заданная система (а); диаграмма перемещений (б)
При построении диаграммы перемещений мы учтем, что система деформируется симметричным образом, поэтому
l1 l2 cos .
Так как стержень 1 не нагревается, то l1 E1l1 , но
l2 2l2 l2 t t0 .
E
Вставив эти значения в уравнение деформаций, получим:
l |
|
|
l |
2 l |
|
t t |
|
|
cos , |
1 1 |
|
2 |
|
2 |
0 |
|
|||
E |
E |
|
|
|
|
||||
|
|
|
|
|
|
|
|||
или |
|
|
|
|
|
1 |
|
|
|
2 E t t0 |
|
|
. |
|
|||||
|
|
|
|
|
cos2 |
|
|
||
40
