
Расчетно-проектировочные работы и примеры их выполнения. Методическое пособие для студентов дневных / Основныезадачи 1-го семестра
.pdf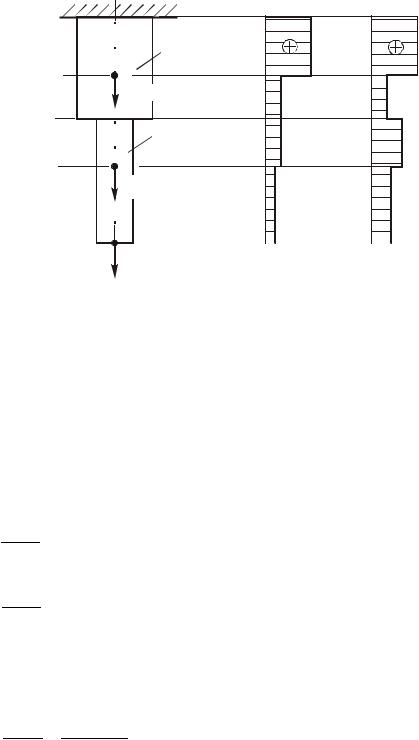
NCD Р1 Р2 10 5 15кН .
N DE Р1 Р2 Р3 10 5 30 45кН .
|
|
|
А =10см2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
2 |
45 |
45 |
||||
|
|
Р =30кН |
|||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
3 |
|
|
|
15 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
А =5см2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
|
|
1 |
15 |
30 |
||||
|
|||||||||
|
|
|
|||||||
|
|
|
Р =5кН |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
2 |
|
|
10 |
|
|
20 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
Р =10кН |
N, кН |
, МПа |
||||
|
1 |
|
|
|
|
|
|
||
|
а) |
|
б) |
|
в) |
||||
Рис. 1.8. К построению эпюр продольных сил и нормальных напряжений в поперечных сечениях бруса а) схема бруса; б) эпюра продольных сил; в) эпюра нормальных напряжений
1.3. По найденным значениям продольных сил строим эпюру N
(рис. 1.8, б).
2.Вычисляем нормальные напряжения, действующие в поперечных сечениях бруса участков AB, BC, CD и DE:
|
AB |
|
N AB 10 103 |
20 106 Па 20 |
МПа, |
|||
|
|
АAB |
5 10 4 |
|
|
|
|
|
|
BC |
|
NBC 15 103 |
30 106 Па 30 |
МПа, |
|||
|
|
АBC |
5 10 4 |
|
|
|
|
|
|
CD |
|
NCD |
15 103 |
|
15 106 |
Па 15 МПа, |
|
|
|
АCD |
10 10 4 |
|
|
|
||
|
DE |
|
NDE |
45 103 |
|
45 106 |
Па 45 МПа. |
|
|
|
АDE |
10 10 4 |
|
|
|
||
Эпюра нормальных напряжений представлена на рис. 1.8, в.
На рис. 1.8, б и 1.8, в можно видеть, что эпюра продольных сил имеет два скачка - в сечениях B и D, где приложены внешние силы, а эпюра нормальных напряжений – три: в сечениях B и D, где приложены внешние силы и в месте изменения площади поперечного сечения (сечение С).
11
1.4. Деформации и перемещения
Рассмотренный в предыдущем параграфе вопрос об определении нормальных напряжений теснейшим образом связан с расчетами бруса и шарнирно-стержневых систем (например, ферм) на прочность. Умение вычислять деформации и перемещения необходимо для расчетов на жесткость, а также для определения сил в статически неопределимых системах.
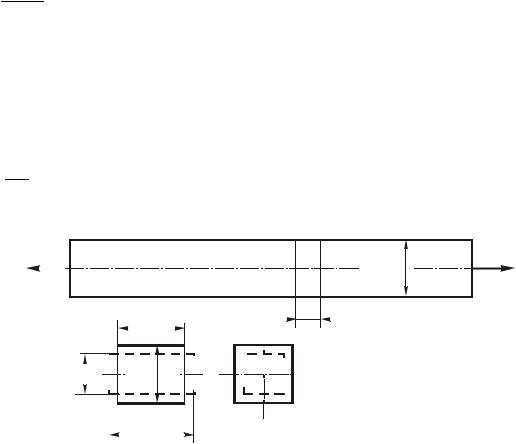
Выделим из бруса, изображенного на рис. 1.9, а, бесконечно малый элемент длиной dz. Этот элемент отдельно изображен (в двух проекциях) на рис. 1.9, б; штриховыми линиями он показан в деформированном состоянии (при растяжении) – длина элемента увеличилась, а размеры поперечного сечения уменьшились (при сжатии наблюдается обратная картина). Приращение длины элемента обозначим dz - абсолютное удлинение. Отношение приращения (изменения) длины элемента к его первоначальной длине называется
относительным удлинением или продольной деформацией:
|
dz . |
(1.2) |
|
dz |
|
Очевидно, что относительное удлинение – безразмерная величина. В некоторых случаях ее выражают в процентах. При растяжении продольную деформацию считают положительной, а при сжатии – отрицательной.
Отношение изменения а размера поперечного сечения к его первоначальному значению называют относительным поперечным сужением
(расширением) или поперечной деформацией:
aa .
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dz |
|
|
|
|
|
dz |
|||||||
б) |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
a-a |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
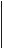 dz+ (dz)
dz+ (dz)

 a
a
(1.3)
P
Рис. 1.9. Деформации при растяжении бруса (а); проекции малого элемента бруса (б)
При растяжении поперечные размеры бруса уменьшаются и по принятому правилу знаков – величина отрицательная.
Продольную и поперечную деформации называют также линейными деформациями (общее наименование).
12

Для подавляющего большинства конструкционных материалов с достаточной для практики точностью можно считать, что в известных
пределах нагружения между продольной деформацией и соответствующим (действующим в ее направлении) нормальным напряжением существует прямо пропорциональная (линейная) зависимость.
Это положение носит название закона Гука и записывается в виде |
|
E . |
(1.4) |
Коэффициент пропорциональности Е называют модулем продольной упругости (другие названия: модуль нормальной упругости; модуль упругости; модуль упругости 1-го рода; модуль Юнга). Очевидно, Е имеет ту же размерность, что и напряжение, т.е. выражается в Па или МПа.
Модуль продольной упругости – физическая постоянная данного материала, характеризующая его жесткость. Чем жестче материал, тем меньше он деформируется при данном напряжении.
Для каждого материала модуль продольной упругости колеблется в узких пределах. Например, для стали E 1,9...2,15 105 МПа. При этом весьма важно иметь в виду, что значение Е для стали практически не зависит от ее химического состава и термической обработки.
Опытным путем установлено, что при простом растяжении или сжатии отношение поперечной деформации к продольной – величина постоянная для данного материала. Это отношение, взятое по абсолютному значению,
называется коэффициентом поперечной деформации или коэффициентом
Пуассона: |
|
|
|
. |
(1.5) |
|
|
|
Значения коэффициента Пуассона для различных материалов находятся в пределах от 0 до 0,5.
Минимальное значение коэффициент Пуассона имеет для пробки 0 ; максимальное – для каучука 0,5 . Для большинства металлов и сплавов
значение коэффициента Пуассона колеблется в сравнительно узких пределах: от 0,23 до 0,35 (в среднем примерно 0,3).
Перейдем к вопросу об определении изменения длины (удлинения или укорочения) бруса. Из выражения (1.2) имеем dz dz изменение длины бесконечно малого элемента, а из выражения (1.4) – закон Гука
E
и
dz dz dz .E
Нормальное напряжение, возникающее в поперечном сечении бруса, выразим через продольную силу и площадь сечения:
13
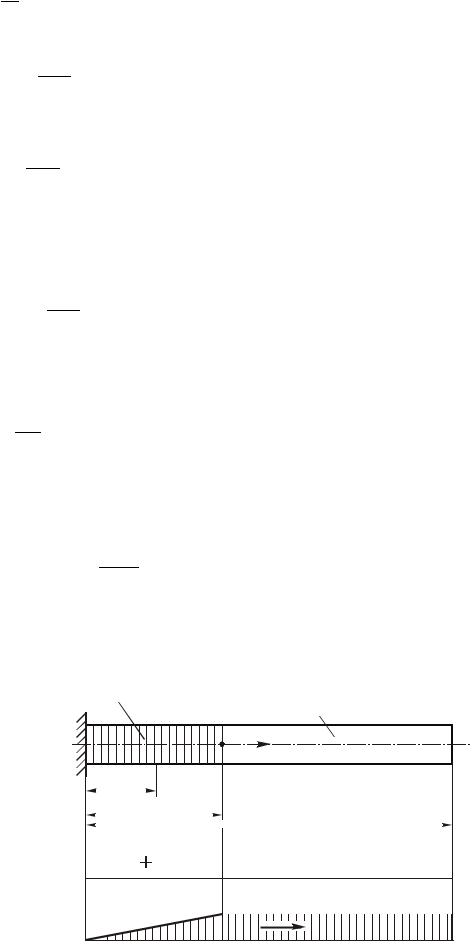
NA .
Подставляя значение в выражение для dz получаем
dz |
Ndz . |
(1.6) |
|
EA |
|
Для определения изменения длины l всего бруса (или участка бруса) следует просуммировать значения dz по всей длине, т.е. взять интеграл
l |
|
Ndz . |
(1.7) |
|
EA |
|
|
|
l |
|
|
В наиболее общем случае, когда законы изменения N и А (или одной из этих величин) различны для отдельных участков бруса, при определении l интегрирование ведут в пределах каждого из участков, а затем результаты алгебраически суммируют:
k |
Ndz . |
|
l |
(1.8) |
|
i 1 l |
EA |
|
i |
|
|
В частном случае (см. рис. 1.9, а), когда поперечное сечение бруса или отдельного его участка постоянно и продольная сила во всех сечениях одинакова, из (1.7) получаем
l |
Nl . |
(1.9) |
|
EA |
|
Выражение (1.9) часто называют формулой Гука, а произведение EA условно называют жесткостью сечения бруса при растяжении (сжатии).
Изменение длины бруса (удлинение или укорочение) равно алгебраической сумме удлинений (укорочений) отдельных участков:
k |
k |
N |
l |
|
|
l |
li E |
|
iAi . |
(1.10) |
|
i 1 |
i 1 |
|
i i |
|
|
В случаях, когда поперечное сечение бруса или продольная сила или обе эти величины изменяются по его длине непрерывно, удлинение (укорочение) бруса следует вычислять по формуле (1.7).
|
Деформируемая |
|
|
|
|
||||
|
|
часть бруса |
|
A |
|||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
P |
|
z |
|
A z |
|
B |
|
|
C |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
a |
l |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
F




 Эпюра N
Эпюра N
Эпюра
 C
C
14

Рис. 1.10. Перемещения при растяжении бруса
При растяжении (сжатии) бруса его поперечные сечения перемещаются в направлении оси. Перемещения являются следствием деформаций, но эти понятия необходимо строго разграничивать. Например, в случае, представленном на рис. 1.10, деформируется лишь левая часть бруса (участок АВ), а участок ВС перемещается как абсолютно твердое тело. Перемещения всех сечений этого участка одинаковы и равны удлинению части АВ бруса:
B C lAB EAPa .
Перемещение произвольного сечения бруса равно изменению длины участка, заключенного между этим сечением и заделкой.
Например, для сечения, отстоящего на расстоянии z от заделки (рис. 1.10),
z lz EaPz ,
где z a .
График z f z показывающий перемещения поперечных сечений в
функции их расстояния z от неподвижного конца бруса (или сечения, условно принятого за неподвижное), называется эпюрой перемещений (рис. 1.10); стрелкой на эпюре показано направление перемещений.
Остановимся на определении перемещений узлов (шарниров) стержневых систем.
Эти перемещения определяют по известным удлинениям и укорочениям стержней, сходящихся в рассматриваемом узле.
Пусть, например, требуется найти перемещение шарнира А кронштейна, изображенного на рис. 1.11, а.
Вырезая узел А и составляя для него два уравнения равновесия ( U 0 иV 0 ), находим силы в стержнях (рис. 1.11, б). Очевидно, сила N1 – растягивающая, N2 – сжимающая. По формуле Гука находим изменения длин стержней.
15
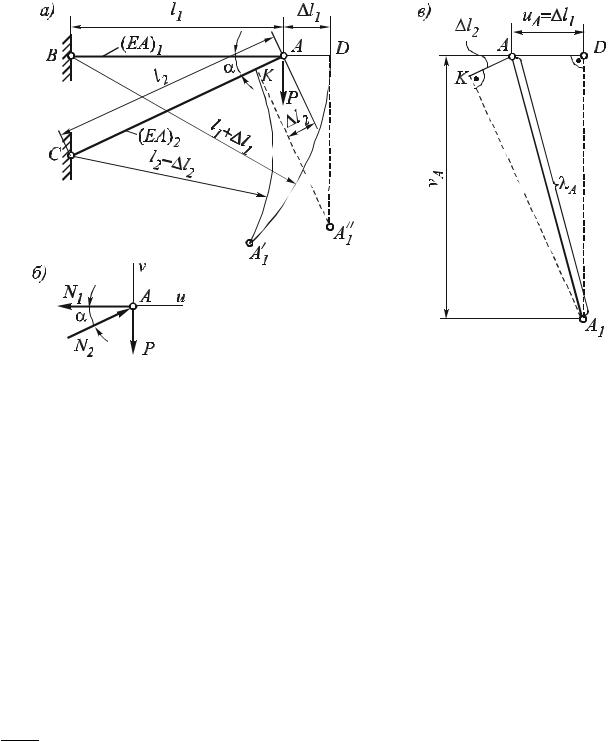
Рис. 1.11. Расчетная схема кронштейна (а); схема определения усилий (б); диаграмма перемещений узла А (в)
Для нахождения положения шарнира А после деформации следует мысленно разъединить стержни, отложить по их направлениям величины l1 и
l2 (отрезки AD и AK на рис. 1.11, а) и, вращая стержни вокруг центров В и С,
вновь свести их вместе.
Таким образом, положение шарнира А после деформации (точка A1 )
находится на пересечении дуг, проведенных из центров В и С радиусами l1 l1 и l2 l2
Построение, показанное на рис. 1.11, а, выполнено со значительным нарушением масштабов: отрезки AD и AK, изображающие изменения длин l1
и l |
2 |
стержней примерно равны соответственно 1 |
и |
1 от величин l и |
l |
2 |
, в |
|
|
5 |
|
15 |
1 |
|
|
||
|
|
|
|
|
|
|
||
то время как фактически упругие удлинения стальных стержней не превышают
1 |
от их длины. |
1000 |
|
В силу малости удлинений (укорочений) можно заменить дуговые засечки перпендикулярами, проведенными из точек D и K к направлениям стержней, и считать новым положением шарнира точку A1 . Если бы удалось выполнить
рассмотренные построения без искажения масштабов (для этого потребовался бы лист бумаги весьма больших размеров – порядка 2 1м), можно было бы
убедиться, что дуговые засечки и перпендикуляры практически сливаются. Достоинством указанного построения, называемого диаграммой
перемещений, является его простота и возможность выполнения в
16
произвольном масштабе, не связанном с масштабом чертежа самой стержневой системы.
Диаграмма перемещений может быть построена отдельно, как показано на рис. 1.11, в; при этом, если построение выполнено в достаточно крупном масштабе, можно не устанавливать аналитической зависимости между l1 , l2
и перемещением узла А, а замерив отрезок диаграммы AA1 и умножив его на
масштаб, получить искомое перемещение. На этом же чертеже показаны горизонтальная uA и вертикальная A составляющие полного перемещения.
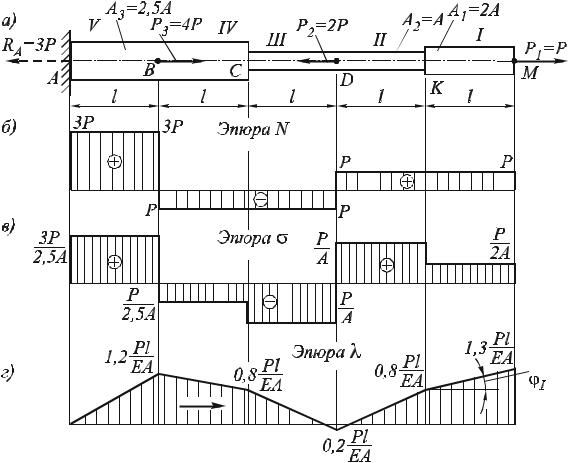
Пример 1.4. Для бруса, изображенного на рис. 1.12, а, построить эпюры:
1.продольных сил и нормальных напряжений;
2.перемещений поперечных сечений по длине.
Решение.
1.1.Разбиваем брус на участки, начиная от свободного конца. Границы
участков проходят через точки приложения внешних сил и места изменения размеров поперечного сечения.
1.2. Строим эпюры продольных сил (рис. 1.12, б) и нормальных напряжений (рис. 1.12, в), как изложено выше в примерах 1.1, 1.2 и 1.3.
Рис. 1.12. Расчетная схема бруса (а); эпюра продольных сил (б); эпюра нормальных напряжений (в); эпюра перемещений (г)
2. Строим эпюру перемещений.
Определяем перемещения сечений, совпадающих с границами участков, так как между указанными сечениями эпюра линейна.
17

Сечение А неподвижно, т.е. A 0 (построение эпюры перемещений
следует всегда начинать от неподвижного или условно принятого неподвижным сечения).
Перемещение сечения В равно изменению длины (в данном случае удлинению) участка АВ (участка V) бруса:
B lV E N2V,5l A E 32Pl,5A 1,2 EAPl .
Сечение В перемещается вправо; соответствующую ординату условно будем считать положительной и отложим (в выбранном масштабе) вверх по оси эпюры (рис. 1.12, г).
Перемещение сечения С равно алгебраической сумме изменений длин участков V и IV бруса:
C lV lIV E N2V,5l A EN2IV,5lA E 32Pl,5A E Pl2,5A 0,8 EAPl .
То же самое можно записать несколько компактнее:
C B lIV 1,2 EAPl E Pl2,5A 0,8 EAPl .
Сечение С также перемещается вправо. Аналогично,
D C lIII C NEAIII l 0,8 EAPl EAPl 0,2 EAPl .
Знак минус указывает, что сечение D перемещается влево (так как ранее было принято считать перемещения вправо положительными).
Значения K и M указаны на эпюре (рис. 1.12, г).
Пример 1.5. По данным предыдущего примера построить эпюры перемещений от действия каждой из сил в отдельности.
Решение.
1. При действии силы P1 P (рис. 1.13, а) деформируется (растягивается)
весь брус. Границами участка служат сечения С, K, M – места изменения размеров поперечного сечения; перемещения этих сечений:
СР |
|
P 2l |
0,8 Pl ; |
|
|
|
|
|
|
||
1 |
|
E 2,5A |
|
EA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
KР |
CР |
P 2l |
0,8 |
Pl |
P 2l |
2,8 |
Pl ; |
||||
1 |
|
1 |
|
EA |
|
EA |
EA |
|
|
|
EA |
MР |
KР |
|
Pl |
2,8 Pl |
0,5 |
|
Pl |
3,3 Pl . |
|||
1 |
|
1 |
|
E 2A |
EA |
|
EA |
|
EA |
||
|
|
|
|
|
|
||||||
Соответствующая эпюра дана на рис. 2.13, б.
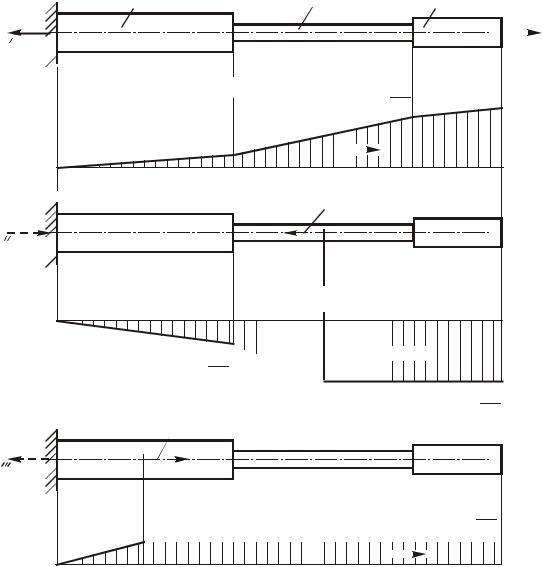
1. При действии силы P2 (рис. 1.13, в) сжимаются участки АС и CD бруса;
эпюра перемещений дана на рис. 1.13, г. Участки DK и KM не деформируются, и все поперечные сечения этих участков перемещаются влево вместе с сечением D.
18
a)
RA=P  A
A
б)
в)
RA=2P A
A
г)
д)
RA=4P
A
e)
2,5А |
A |
2A |
|||||||
|
|
|
|
|
|
|
P=P |
||
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
M |
||
|
|
|
|
K |
|||||
|
|
|
|
|
|||||
Эпюра |
|
|
|
Pl |
3,3 Pl |
||||
P |
|
|
|
EA |
|||||
1 |
|
|
2,8EA |
||||||
0,8 Pl |
|
|
|
|
|
|
|
||
EA |
|
|
|
|
|
|
|
|
|
|
P2=2P |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
C |
|
D |
|
|
M |
||||
|
K |
||||||||
|
|
|
|
|
|||||
Эпюра P2
1,6EAPl 


3,6 EAPl
P3=4P
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
M |
|
B |
|
K |
|||||
|
|
||||||
|
|
Эпюра P |
|
1,6 Pl |
|||
|
3 |
|
EA |
||||
|
|
|
|
|
|
|
|
Рис. 1.13. Схема бруса (а) и эпюра перемещений (б) при нагрузке P1 P ; схема бруса (в) и эпюра перемещений (г) при силе P2 2P ; схема бруса (д) и эпюра перемещений (е) при нагрузке P3 4P
3. Сила P3 растягивает участок АВ бруса (рис. 1.13, д); эпюра перемещений
дана на рис. 1.13, е.
На всех эпюрах стрелки указывают направления перемещений.
Если просуммировать все три эпюры перемещений, получим, как это следует из принципа независимости действия сил, эпюру от совместного действия всех заданных сил (эпюру, представленную на рис. 1.12, г).
Пример 1.6. Определить удлинение бруса постоянного поперечного сечения, нагруженного равномерно распределенной нагрузкой интенсивностью q (рис. 1.14).
Решение.
19

Определим продольную силу, возникающую в произвольном поперечном сечении бруса. Применяя метод сечений и рассматривая условие равновесия нижней оставленной части длиной z (рис. 1.14), получим
N qz ,
где qz – равнодействующая распределенной нагрузки, действующей на оставленную часть.
q
l
u  z
z
Эпюра N Эпюра
z |
ql |
|
 N
N
q |
ql2 |
|
2EA |
Рис. 1.14. Брус постоянного сечения, нагруженный равномерной нагрузкой q
Так как продольная сила переменна – изменяется по длине бруса по линейному закону (см. эпюру N на рис. 1.14), то удлинение определяем по формуле (1.7):
l |
Ndz |
l |
qz |
dz |
ql 2 |
. |
l |
EA |
|
|
2EA |
||
0 |
0 |
EA |
|
|||
|
|
|
|
|
||
Учитывая, что ql G равнодействующая всей нагрузки, действующей на
брус, выражение для l можно записать так:
l 2GlEA .
Итак, удлинение бруса постоянного сечения от действия равномерно распределенной по его длине нагрузки вдвое меньше, чем удлинение от сосредоточенной силы, равной равнодействующей этой нагрузки и приложенной к свободному концу бруса.
Примером равномерно распределенной осевой нагрузки может служить собственная сила тяжести бруса, при этом q A и G Al – сила тяжести
(вес) всего бруса.
Перемещение произвольного поперечного сечения бруса, отстоявшего на расстоянии u от свободного конца, равно удлинению части бруса, заключенного между заделкой и этим сечением:
l |
qz dz |
qz |
2 |
l |
q |
l2 u2 ; |
|
|
|
||||
u |
EA |
2EA |
u |
2EA |
|
|
|
|
|
|
|
||
т.е. перемещения изменяются по квадратичному закону; эпюра - парабола
(рис. 1.14).
20
