14)Геометрические характеристики сечений. Моменты инерции относительно параллельных осей.
Способность бруса сопротивляться деформации изгиб, кручение и др. зависит не только от свойств материала и его размеров, но и от формы поперечного сечения (при деформации растяжение, сжатие еще и от площади). Геометрические параметры, учитывающие параметры геометрических сечений:
-Sy,Sz-статические моменты площади
-Jy,Jz,Jyz,Jp-моменты инерции поперечного сечения
-WyWz,Wp-моменты сопротивления поперечных сечений
Статический момент площади А относительно оси у. Это геометрическая хар-ка определяемая интегралом вида; Sy=∫AZdA, аналогично Sz=∫AydA [СМ³],[М³]. Если известны координаты центра тяжести плоских фигур: Sy=Zцентра тяжести• Α, Sz=Уц.т.•А, и наоборот Zцִт=Sy/A,yц.т..=Sz/A
Статический момент площади относительно оси проходящей через центр тяжести фигуры равен 0
Центральные оси -это оси проходящие через центр тяжести фигуры
Моменты инерции:
a)Осевые
Jz=∫Ay2dA-момент инерции относительно оси z
Jy=∫Az2dA-момент инерции относительно оси y [M4],[CM4]
b)Центробежный момент инерции.
Главные оси плоской фигуры –Jzy=∫AzydA-это оси относительно которых центробежный момент инерции =0,>0,<0
c)Полярный
Jρ=∫Aρ2dA={ρ2=z2+y2}=∫Az2dA+∫Ay2dA=Jy+Jz
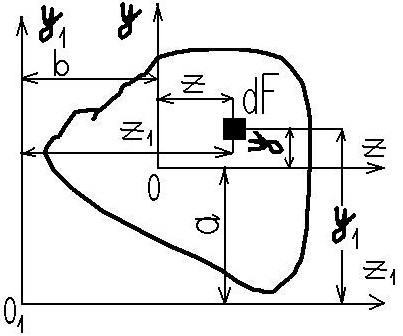
Пусть известны моменты инерции бесконечно малой фигуры dF относительно центральных осей Z,y;
Jz=∫Fy2dF-момент инерции относительно оси z
Jy=∫Fz2dF-момент инерции относительно оси y
Jyz=∫FzydF
Определим моменты инерции относительно осей, параллельных центральным;
Jy1z1=∫Fz1y1dF
Jy1=∫Fz21dF
Jz1=∫Fy21dF
Координаты любой точки в новой системе z1O1y1 можно выразить через координаты в старых осях так;
z1=z+b, y1=y+a
Подставляем эти значения в формулы (те которые выше) и интегрируем почленно;
Jz1=∫Fy21dF=∫F(y+a)2dF= =∫Fy2dF+a2∫FdF+2a∫FydF
Jy1=∫Fz21dF=∫F(z+b)2dF= =∫Fz2dF+b2∫FdF+2b∫FzdF
Jy1z1=∫Fz1y1dF=∫F(z+b)(y+ +a)dF+ab∫FdF+a∫FzdF+b· ·∫FydF
Так как интегралы ∫FdF= =SZ,∫FzdF=Sy равны нулю как статические моменты относительно центральных осей, то формулы принимают вид;
JZ1=JZ+a2F
Jy1=Jy+b2F
Jz1y1=Jzy+abF
Cследовательно; 1) моменты инерции фигуры относительно любой оси равен моменту инерции относительно центральной оси, параллель- ной данной, плюс произведение площади фигуры на квадрат рас- стояния между этими осями. 2)центробежный момент инерции относительно любой системы прямоугольных осей равен центробежному моменту относительно системы центральных осей, параллельных данным, плюс, произведение площади фигуры на координаты ее центра тяжести в новых осях.
Р.S.Координаты а,b, входящие в формулу следует подставлять с учетом их знака.
15)Вычисление момента инерции при повороте осей. Главные оси инерции и главные моменты инерции.
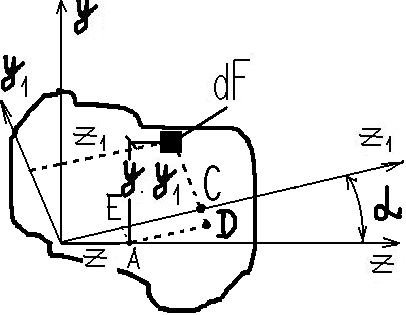
Пусть известны моменты инерции бесконечно малой фигуры dF относительно центральных осей Z,y;
Jz=∫Fy2dF-момент инерции относительно оси z
Jy=∫Fz2dF-момент инерции относительно оси y
Jyz=∫FzydF
Повернем оси у,z на угол α против часовой стрел- ки, считая угол поворота осей в этом направлении положительным. Определим моменты инерции сечения относительно повернутых осей z1,y1;
Jy1z1=∫Fz1y1dF
Jy1=∫Fz21dF
Jz1=∫Fy21dF
Координаты произвольной элементарной площадки в новых осях z1,y1 выражаются через координаты z,y прежней системы осей следующим образом;
Z1=OC+AD=zcosα+ysinα
y1=CB=BD-EA=ycosα-zsinα
Подставим эти значения в формулы моментов инерции (выше) и проинтегрируем почленно;
Jz1=∫F(ycosα-zsinα)2dF= =c =cos2α∫Fy2dF+sin2α∫FZ2dF- -sin2α∫FyzdF
Jy1=∫F(zcosα+ysinα)2dF= =sin2α∫Fy2dF+cos2α∫FZ2dF+sin2α∫FzydF
Jy1z1=∫F(zcosα+ysinα)(ycosα-zsinα)dF=(cos2α-sin2α) ∫FzydF+(1/2)sin2α(∫Fz2dF-∫Fz2dF)
Окончательно находим;
Jz1=Jzcos2α+Jysin2α-Jzysin2α
Jy1=Jycos2α+Jzsin2α-Jzysin2α
Jz1y1=Jzycos2α-(1/2)(Jy-Jz)· ·sin2α
Опр. гл. осей и гл. моментов инерции.
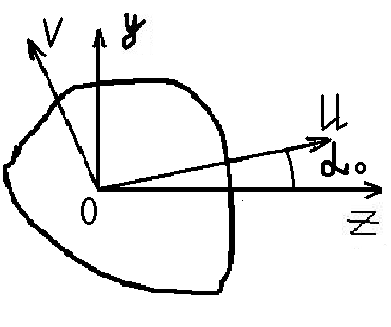
Наибольшее значение имеют главные центральные оси, центробежный момент инерции относительно которых равен нулю.
JUV=0
Чтобы определить положение главных центральных осей повернем произвольную начальную систему центральных осей z,y на некоторый угол α0, при котором центробежный момент инерции становится равным нулю;
Jz1y1=JVU=0
Тогда из формулы
Jz1y1=Jzycos2α-(1/2)(Jy-Jz)·sin2α
получим
Jz1y1=Jzycos2α0-(Jy -Jz)2(sin2α0)
Откуда
tg2α0=2Jzy/Jy-Jz
Откуда найдем два угла (острый и тупой) отличающиеся на 90 градусов. Откладываем от оси z и получаем положение оси U (ось V перпендикулярна U)Значения главных моментов инерции из формул;
Jz1=Jzcos2α+Jysin2α- Jzysin2α
Jy1=Jycos2α+Jzsin2α-Jzysin2α, прехода к повернутым осям, приняв α=α0
Jz1=Jzcos2α0+Jysin2α0 -Jzysin2α0
Jy1=Jycos2α0+Jzsin2α0-Jzysin2α0
Если исключить α0 из трех уравнений (Jz1,Jy1, Jz1y1), то получим формулу для вычисления моментов инерции относительно главных центральных осей.
JU=1/2[(Jz+Jy)±√(Jz-Jy)2+4J2zy]
JV=1/2[(Jz+Jy)±√(Jz -Jy)2+4J2zy]
Свойства главных центральных осей;
1)относительно этих осей центробежный момент инерции равен 0
2)относительно V,U моменты инерции имеют экстремальные величины
3)если плоская фигура имеет ось симметрии, то эта ось одна из главных центральны, вторая проходит через центр тяжести фигуры и перпендикулярна первой.