23)Внецентренное растяжение (сжатие) брусьев. Ядро сечения.

Деформацию и внецентренное растяжение (сжатие) вызывают внешние силы, результирующие которых параллельны продольной оси, но не совпадают с ней.

Внутренние силовые факторы определяем из уравнений равновесия отсеченной части:

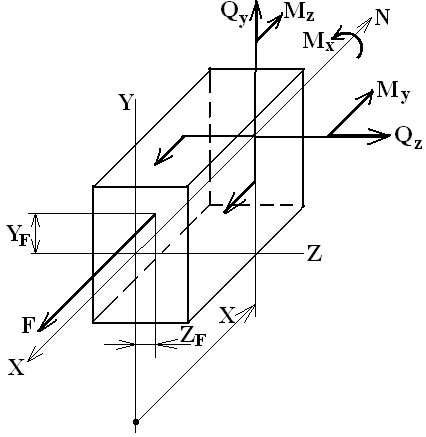
1. F_x=0: N(x)-F=0; N(x)=F;

2. F_y=0: Q_y(x)+0=0; Q_y(x)=0;

3. F_z=0: Q_z(x)+0=0; Q_z(x)=0

4. mom_x=0: M_x(x)+0=0; M_x(x)=0

5. mom_y=0: M_y(x)-F∙z_F=0; M_y(x)=F∙z_F;

6. mom_z=0: M_z(x)-Fy_F=0; M_z(x)=Fy_z;

Следовательно, брус испытывает пространственный изгиб с растяжением. По принципу суперпозиции:

σ =σ⁽¹⁾+σ⁽²⁾+σ⁽³⁾=(F/A)∙[1±y_Fy/i²_z± z_Fz/i²_y] – формула для вычисления напряжен. в точке с координ. z, y. Для проведения расчета на прочность необходимо знать величины max напряжений σ_max растягивающих и сжимающих. Для этого необходимо знать координаты точек max удаленных от нейтральной линии. Получим уравнение нейтральной линии. При внецентренном растяжении пользуются формулами:

σ =(F/A)∙[1+y_Fy/i²_z+z_Fz/i²_y]. При сжатии:

σ =(–F/A)∙[1+y_Fy/i²_z+z_Fz/i²_y]. Знак перед слагаемыми изгиба ставится в зависимости от того, каким волокнам, растянутым или сжатым, принадлежит рассматриваемая точка.

Нейтральная линия – линия в поперечном сечении во всех точках которой σ =0. Следовательно:

(F/A)∙[1+y_Fy/i²_z+z_Fz/i²_y]=0;

z/a_z+y/a_y=1 – уравнение нейтральной линии в отрезках, где a_z=–i²_y/z_F; a_y=–i²_z/y_F.

Ядро сечения такая область в окрестности ц.т. сечения, что если внутри нее приложить внешнюю силу, напряжения в сечении будут одного з-н. Чтобы построить ядро сечения нужно «обкатать» н.л. вокруг сечения, т.е. размещать н.л. так, чтобы она касалась контура сечения, негде не пересекая его. При этом точка приложения силы даст контуры ядра сечения. Пример ядра сечения:

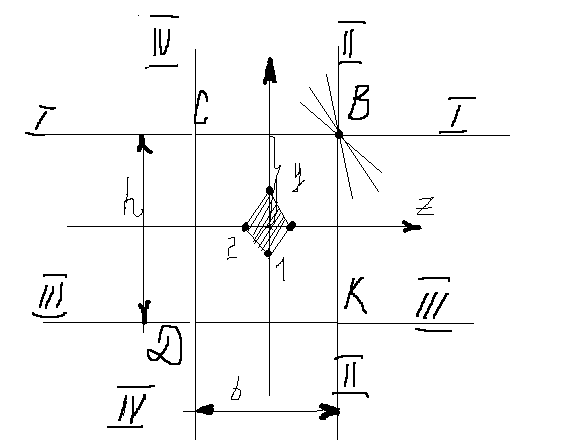
24)Основы напряженного состояния в точки. Главные площадки и главные напряжения. Прямая и обратные задачи. Линейное напряженное состояние.

Через произвольную точку тела можно провести бесчисленное множество сечений, на которых возникает напряжение σ и τ, в общем случае отличающиеся друг от друга в зависимости от ориентации площадки. Совокупность напряжений, возникающих на множестве площадок, проведенных через рассматриваемую точку, называют напряженным состоянием в точке.

В окрестности точки В вырезаем элементарные параллелепипед. Поворачивая элементарный параллелепипед вокруг т.В, можно найти такое его положение, при котором на гранях действует только нормальное напряжение, а касательное будет равным 0. Теория упругости доказывает, что для любого тела при любой нагрузке для любой точки можно найти такую ориентацию параллелепипеда, и это будет единственное его положение. Такие площадки, на которых действуют нормальные напряжения, называются главными. Напряжения σ на этих площадках – главные напряжения. Направления σ – главные направления. Р – полное напряжения на рассматриваемой площадке. Если в задаче одно из главных напряжений не равно 0, то такие задачи называются одноосными или линейными. Если не равны 0 два главные напряжения – двухосные или плоские. Если не равны 0 три главные напряжения – трехосные или пространственные.

Прямая задача:

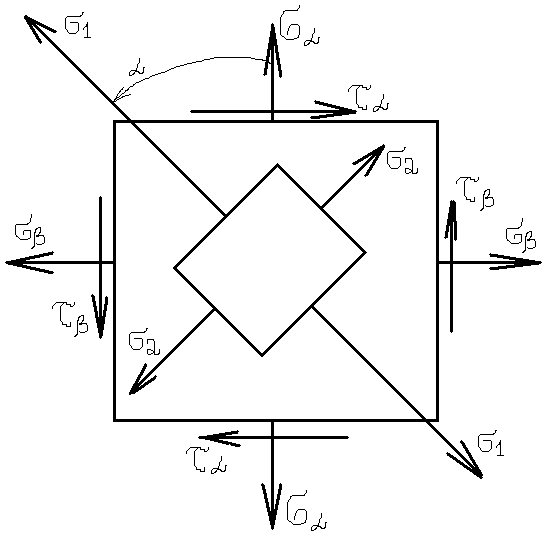
n_α – нормаль к площадке А_α; n – нормаль к площадке наибольшего главного напряжения; α – острый угол между n_α и n, причем если поворот от n к n_α по часовой стрелке, то α – отрицательный, если против – положительный.

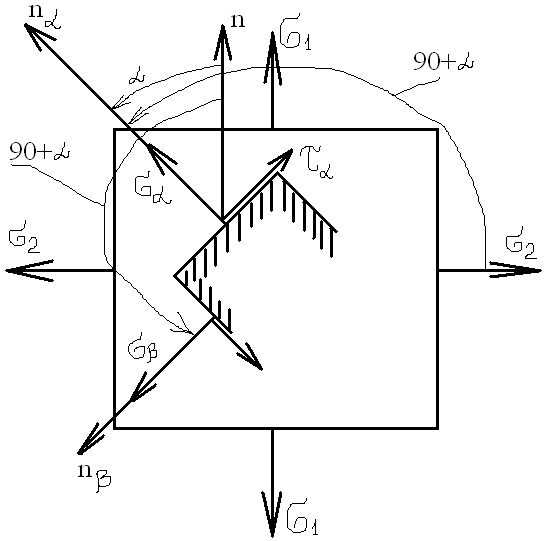
Дано: σ₁; σ₂; α.

Определить: σ_α, τ_α, σ_β, τ_β.

σ_α – результат действия σ₁ и σ₂.

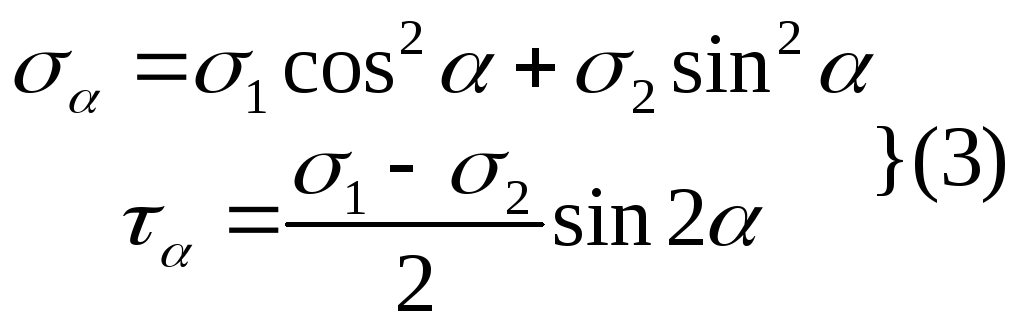
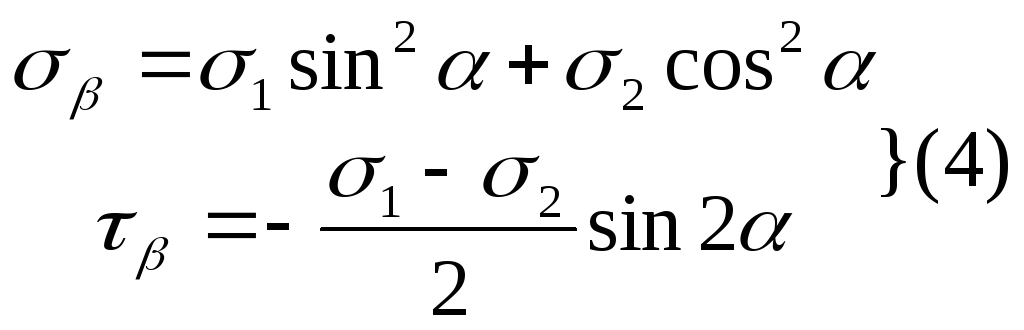
Обратная задача:

Дано: σ_α, τ_α, σ_β, τ_β.

Найти: σ₁; σ₂; α.

Решая совместно системы (3) и (4) получим:

σ₁=½[(σ_α+σ_β)+√((σ_α–σ_β)+4τ²α)];

σ₂=½[(σ_α+σ_β)–√((σ_α–σ_β)+4τ²α)];

σ₁ – напряжение алгебраически больше из двух полученных. Если одно из двух чисел отрицательно, то имеем σ₁ и σ₃. Если оба отрицательны, то σ₂ и σ₃. Если α отрицательное, то по часовой стрелке. Если α положительное, против часовой. Получаем направление σ₁, т.е. наибольшее главное напряжение.

Линейное напряженное состояние.

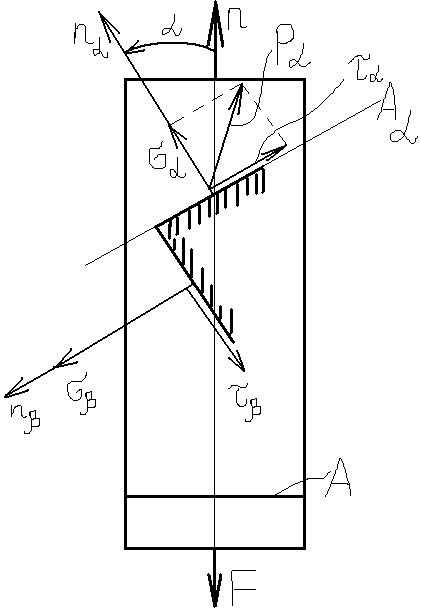
n_α – нормаль к сечению А_α; n – нормаль к поперечному сечению; α – положительное – против часовой стрелки; σ – положительное – направлена вдоль внешней нормали к рассматриваемой площадке; τ – положительное – если стремится повернуть рассматриваемый элемент по часовой стрелке относительно любой точки внутри его.

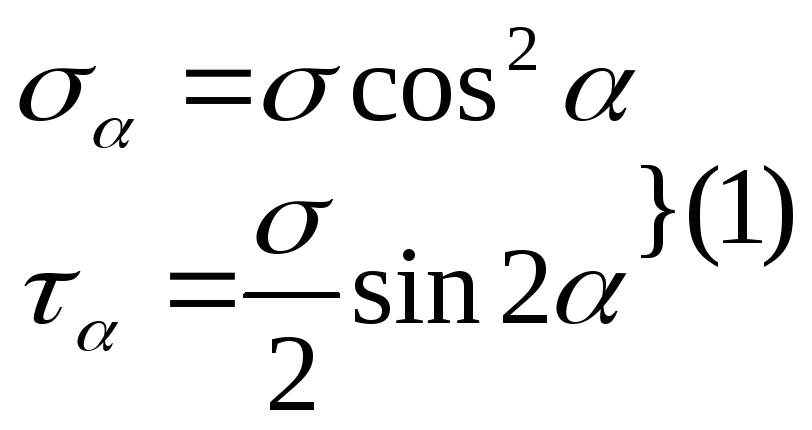
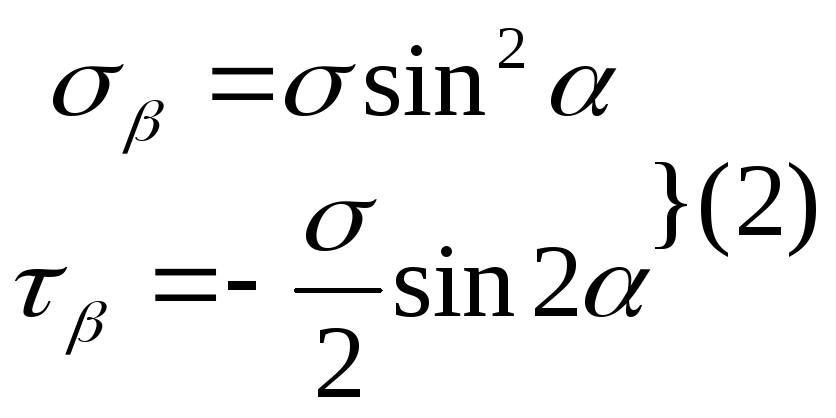
Сумма напряжений на двух взаимно перпендикулярных наклонных площадках всегда равна напряжению в поперечном сечении, независимо от ориентации площадки. Наибольшее касательное напряжение возникает на площадках под углом 45 градусов к главным.