28)Энергия деформации при изгибе. Теорема Кастильяна.

Пусть балка нагружена системой сил Т и силой F. Требуется определить перемещение точки под силой F в ее направлении.

Определим потенциальную энергию деформации балки силами Т и F, которая равна работе, совершаемой этими силами на перемещениях точек, в которых силы приложены.

Запишем выражение для U (потенц. энергия) с учетом последовательности нагружения балки внешними силами.

1) К балке прикладываем силу F, тогда потенциальная энергия деформации системы силой F: U_F=½FΔ_FF.

2) Прикладываем систему сил Т, под действием которой точка под силой F получит дополнительное перемещение Δ_FT. Сила F на перемещение Δ_FT совершает работу : А_FT= FΔ_FT

(Нет 1\2, т.к. сила F уже имела конечное значение; есть 1/2, если сила статически приложена, т.е. во время совершения работы она увеличивается от 0 до конечного значения без рывков и ударов медленно).

Потенциальная энергия деформации равна работе всех сил на их перемещение: U=А_F+A_FT+U_TT

Где U_TT –потенциальная энергия, накапливаемая балкой в результате ее деформации силами системы Т.

U =½FΔ_FT +FΔ_FT+U_TT

Введем новый параметр: удельное перемещение [δ] – перемещение точки под единичной силой F¯=1Н в направлении ее действия, если вместо силы F приложить единичную силу в ее направлении, то получим перемещение Δ_FF.

Δ_FF=Fδ_FF – связь истинного и удельного перемещения.

U=½F²Δ_FF+FΔ_FT+U_TT

Возьмем частную производную по F от U:

∂U/∂F=Fδ_FF+Δ_FT=Δ_F – полное перемещение точки под силой F в ее направлении от действия всех сил приложенных к балке (F+Т).

Теорема Кастильяна: Перемещение точки под силой в ее направлении, равно частной производной от потенциальной энергии деформации системы по этой силе.

U=_iⁿ₌₁∫_LiM²(x)dx/2EI_Z; Δ_F=∂U/∂F= =_i∫_Li((M(x)/EI_Z)(∂M/∂F)dx).

Метод Кастильяна используют для определения перемещений в оболочках, пластинах, массивах.

Если необходимо найти перемещение точки, в которой не приложена внешняя сила, то

1) В т.К прикладываем фиктивную силу по направлению искомого перемещения (если нужно определить угол поворота θ, то прикладываем фиктивный момент).

2) Записывают выражение М(х) с учетом F_Ф (реакции опор находят с учетом F_Ф).

3) Записывают интеграл метода Кастильяна в который уже включили производную от М(х) по F_Ф, т.е. ∂М(х)/∂F_Ф. В этом интеграле вместо F_Ф пишем нуль.

4) Интегрируем и получаем результат.

29)Потенциальная энергия деформации. Гипотезы прочности.

U=∫(M²(x)dV/(2EI_z)); U равно половине произведения внешней силы на перемещение точки под этой силой (сумме произведений), что есть работа внешних сил на перемещениях точки под ними.

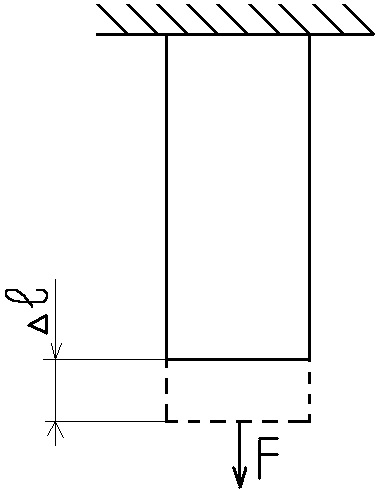
Для одноосного напряженного состояния:

U= ½FΔl; U=½FΔl/(Al)=σε/2= σ²/2E;

При трехосном (пространственном напряженном состоянии):

U=σ₁ε₁/2+σ₂ε₂/2+σ₃ε₃/3=(1/2E)(σ₁²+σ₂²+σ₃²-2υ(σ₁σ₂+σ₂σ₃+σ₃σ₁))

При деформации тела (пространственное) не только происходит изменение его объема, но и изменение формы (кубик → параллелепипед). U=U_V+U_Ф, где U_V – удельная потенциальная энергия изменения объема,

U_Ф – удельная потенциальная энергия формообразования (формоизменения).

U_V=(1-2υ/6E)(σ₁+σ₂+σ₃)²;

U_Ф=(1+υ/6E)((σ₁-σ₂)²+(σ₂-σ₃)²+(σ₃-σ₁)²);

Гипотезы прочности:

Цель теории прочности – сравнить напряженное состояние пространственное, плоское с допускаемыми напряжениями, которые получены экспериментальным путем для одноосного напряженного состояния. Два напряженных состояния (например: трехосное и одноосное) равноопасны, если при увеличении главных напряжений в одно и тоже число раз эти напряженные состояния одновременно становятся предельными. Предельное состояние – состояние потери работоспособности. Для хрупких σ_в → разрушение, для пластичных материалов σ_т → потеря упругих свойств.

Напряжение при напряженном состоянии равно опасное данному трехосному напряженному состоянию называют эквивалентным (σ_экв). При формулировании теории прочности выбирают один или несколько факторов, приводящих к потере работоспособности элемента конструкции (величина напряжений σ, τ, величина деформаций ε, удельная потенциальная энергия, накопленная в теле) разрабатывается теорией, в которых учитывается скорость нагружения, температура, напряженное состояние, давление и т.д.

1-я теория прочности – теория нормальных наибольших напряжений, в соответствии с которой предельное состояние в точке тела наступает, если максимальные σ равны допускаемым. σ_экв1=σ₁. Условие прочности: σ₁≤[σ]. Для 2-х и 3-хосных н.с. дает погрешности, т.к. не учитывается σ₂ и σ₃, но хорошо работает для хрупких материалов.

2-я теория прочности – максимальная относительная деформация ε: предельное состояние наступает, если ε_max превышает допускаемую величину. Условие прочности: ε_max≤[ε]. Не применяется в настоящее время т.к. дает неудовлетворительные результаты.

3-я теория прочности – теория наибольших касательных напряжений: предельное состояние наступает, если, τ_max превышает допускаемую величину τ. При 3-осном состоянии:

τ_max=(σ₁-σ₃)/2;

При 2-осном состоянии:

τ_max=(σ₁-σ₂)/2;

При 1-осном н.с.: [τ]=[σ]/2.

Условие прочности: τ_max≤[τ].

((σ₁-σ₃)/2)≤([σ]/2); σ_экв3≤[σ], где σ_экв3=σ₁-σ₃.

Дает хорошие результаты для пластичных деформаций, но е учитывает σ₂.

4-я теория прочности – энергетическая: предельное состояние наступает, если удельная потенциальная энергия формоизменения превышает допускаемую величину.

U_Ф≤[U_Ф]; U_Ф=(1+υ/6E)((σ₁-σ₂)²+(σ₂-σ₃)²+(σ₃-σ₁)²);

[U_Ф]=((1+υ)2[σ]²)/6E; σ_экв4≤ [σ];

σ_экв4=√(½[(σ₁-σ₂)²+(σ₂-σ₃)²+(σ₃-σ₁)²]);

В настоящее время продолжается разработка теории прочности с целью учета мех. числа факторов, влияющих на работоспособность элементов конструкции и на свойство материалов, т.к. один и тот же материал в зависимости от температуры, скорости нагружения, напряженного состояния и др. ведет себя как хрупкий или пластичный. Чем больше факторов учитывает, тем достовернее результаты, тем меньше коэффициент запаса прочности.