
- •Содержание
- •Лабораторная работа № 1 определение отношения заряда электрона к его массе методом магнетрона
- •Краткая теория
- •Выполнение работы
- •8. При вычислениях используйте следующие данные, характеризующие установку:
- •Выполнение работы
- •1. Устройство и принцип работы модуля «Опыт Франка и Герца»
- •2. Снятие зависимости анодного тока от напряжения на сетке с использованием двухкоординатного графопостроителя н-307/1
- •Контрольные вопросы и задания
- •Рекомендуемая литература
- •Лабораторная работа № 3 изучение неон-гелиевого лазера
- •Краткая теория
- •Устройство Ne-He лазера
- •Механизм образования инверсии в Ne-He лазере
- •Спектр излучения Ne-He лазера
- •Выполнение работы
- •1. Определение длины волны излучения Ne-He лазера
- •2. Исследование распределения интенсивности в лазерном пучке
- •3. Определение расходимости лазерного пучка
- •Контрольные вопросы и задания
- •Рекомендуемая литература
- •Лабораторная работа № 4 изучение сериальных закономерностей в спектре атома водорода
- •Краткая теория
- •Краткое описание установки
- •Выполнение работы
- •Контрольные вопросы и задания
- •Рекомендуемая литература
- •Справочные материалы
- •Лабораторная работа № 5 спектр атома водорода. Атом бора
- •Краткая теория
- •Выполнение работы
- •1. Экспериментальное исследование спектра поглощения
- •1.1. Схема эксперимента
- •1.2. Метод измерения уровней энергии
- •1.3. Исследование спектра. Уровни энергии
- •1.4. Уровни энергии. Параметрическая зависимость
- •2. Обобщенная формула Бальмера. Спектральные серии
- •3. Постулаты Бора
- •4. Система атомных единиц
- •5. Атом водорода
- •5.1. Атом Бора (круговые орбиты)
- •5.2. Атом Бора – Зоммерфельда
- •Контрольные вопросы и задания
- •2. Модель атома по Эрнесту Резерфорду
- •3. Случай многократных столкновений
- •4. Случай однократных столкновений
- •Выполнение работы
- •1. Рассеяние на атоме Томсона
- •2. Рассеяние на атоме Резерфорда
- •3. Рассеяние на многоатомных мишенях
- •4. Расчёт вероятности рассеяния
- •5. Оценка времени экспозиции
- •Контрольные вопросы и задания
- •Рекомендуемая литература
- •Лабораторная работа № 7 изучение спектра атома натрия
- •Краткая теория
- •Экспериментальная установка
- •Выполнение работы
- •Справочные материалы
- •Контрольные вопросы и задания
- •Рекомендуемая литература
Министерство образования и науки Российской Федерации
КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
А.П. БАРКОВ, В.С. ДОРОШ, В.А. НИКИТИН,
В.П. ПРОХОРОВ, Е.Б. ХОТНЯНСКАЯ
ОСНОВЫ АТОМНОЙ ФИЗИКИ
Лабораторный практикум
Краснодар 2012
УДК 539.1 (076.5)
ББК 22.383я73
О753
Рецензенты:
Кафедра физики Кубанского
государственного технологического университета
Доктор физико-математических наук, профессор
Н.М. Богатов
Барков, А.П., Дорош, В.С., Никитин, В.А., Прохоров, В.П.,
Хотнянская, Е.Б.
О753 Основы атомной физики: лаборат. практикум / А.П. Барков,
В.С. Дорош, В.А. Никитин, В.П. Прохоров, Е.Б. Хотнянская.
Краснодар: Кубанский гос. ун-т, 2012. 99 с.
Практикум содержит описание 7 лабораторных работ, краткий теоретический и справочный материал и призван дать наглядное представление студентам об основополагающих явлениях атомной физики. Предлагаются задания к лабораторным работам, контрольные вопросы для самоподготовки, рекомендуемая литература. Две лабораторные работы выполняются на базе учебного компьютерного курса «Физика микромира» Московского государственного университета, цель которых – ознакомить студентов с методикой проведения виртуальных лабораторных работ физического практикума по курсу атомной физики, освоить способы моделирования физических явлений и процессов.
Адресуется студентам физических, радиофизических и физико-технических факультетов университетов.
УДК 539.1 (076.5)
ББК 22.383я73
Кубанский государственный
университет, 2012
Содержание
|
Лабораторная работа № 1.ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ЗАРЯДА ЭЛЕКТРОНА К ЕГО МАССЕ МЕТОДОМ МАГНЕТРОНА . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
|
4
|
|
Лабораторная работа № 2. ОПЫТ ФРАНКА И ГЕРЦА . . . . .
|
13 |
|
|
|
|
Лабораторная работа № 3. ИЗУЧЕНИЕ НЕОН-ГЕЛИЕВОГО ЛАЗЕРА . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
|
29
|
|
Лабораторная работа № 4. ИЗУЧЕНИЕ СЕРИАЛЬНЫХ ЗАКОНОМЕРНОСТЕЙ В СПЕКТРЕ АТОМА ВОДОРОДА . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
|
41
|
|
Лабораторная работа № 5. СПЕКТР АТОМА ВОДОРОДА. АТОМ БОРА . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
|
56
|
|
Лабораторная работа № 6.АТОМНЫЕ МОДЕЛИ ДЖ. ТОМСОНА И Э. РЕЗЕРФОРДА . . . . . . . . . . . . . . . .
|
66
|
|
Лабораторная работа № 7.ИЗУЧЕНИЕ СПЕКТРА АТОМА НАТРИЯ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
|
77 |
Лабораторная работа № 1 определение отношения заряда электрона к его массе методом магнетрона
Цель работы:
– изучить движение электрона при суперпозиции постоянных электрического и магнитного полей;
– измерить зависимость анодного тока от индукции магнитного поля при различных анодных напряжениях и рассчитать удельный заряд электрона;
– оценить погрешности измерений.
Краткая теория
Важнейшими характеристиками электрона являются его заряд и масса. При движении электрона в электрических и магнитных полях траектория электрона определяется конфигурацией этих полей и отношением заряда электрона к его массе.
Если структура электрического или магнитного полей задана и из опыта известна траектория электронов в этом поле, то значение отношения заряда электрона к его массе e/m может быть найдено. На этом соображении основаны теперь многочисленные методы определения отношения заряда к массе для электрона. Впервые этот приём был использован в так называемом методе парабол, когда изучалось отклонение от первоначального направления электронного пучка, пролетающего поперёк однородного электрического поля плоского конденсатора, помещенного в магнитное поле. Аналогичные способы определения величины e/m применяются и в случае ионов и других частиц.
Одним из важнейших вариантов этих методов является метод магнетрона, в котором используется отклонение движущегося электрона магнитным полем.
Магнетрон представляет собой двухэлектродную электронную лампу, в которой электроны, летящие от катода к аноду в электрическом поле, подвергаются воздействию внешнего магнитного поля. Магнетроны служат генераторами электромагнитных волн СВЧ (0,3 – 300 ГГц). Существует несколько типов магнетронов, различающихся между собой параметрами и механизмом возбуждения колебаний.
В настоящей работе используется магнетрон со сплошным анодом, представляющий собой обычный цилиндрический диод в постоянном магнитном поле, направленном вдоль оси диода (см. рис. 1). Найдём распределение потенциала в пространстве между катодом и анодом, для чего воспользуемся теоремой Гаусса – Остроградского:
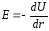 ;
;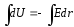 ;
;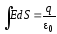 . (1)
. (1)
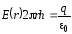 ;
;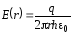 . (2)
. (2)
Подставляя (2) в (1), получаем
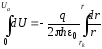 ; (3)
; (3)
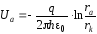 ; (4)
; (4)
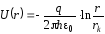 . (5)
. (5)
Поделив (5) на (4), получим
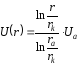 , (6)
, (6)
где Ua – потенциал анода относительно катода.
При rk << rа (см. рис. 1) потенциал весьма быстро нарастает вблизи катода и далее изменяется незначительно.
В силу этого основное изменение скорости электронов будет происходить вблизи катода, и при дальнейшем движении их скорость будет изменяться мало. Таким образом, можно считать, что в пространстве между катодом и анодом электроны движутся в магнитном поле с постоянной скоростью V.
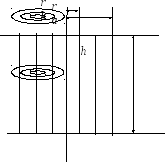
Рис. 1. Схематическое изображение магнетрона
Магнитная составляющая силы Лоренца определяется выражением:
F = e [V B]. (7)
Если считать, что электроны движутся с постоянной скоростью, то сила Лоренца будет являться центростремительной:
 . (8)
. (8)
С увеличением магнитной индукции В радиус траекторий уменьшается. Режим, при котором траектории электронов касаются анода, называется критическим.
При В >> Вкр электроны перестают попадать на анод и анодный ток уменьшается скачком.
На рис. 2 изображены анод (А), катод (К), обмотка соленоида и линии индукции магнитного поля. Характер движения электронов в лампе зависит от индукции магнитного поля, создаваемого соленоидом. На рис. 3 изображены возможные траектории движения электронов.

Рис. 2. Взаимное расположение анода, катода
и магнитного поля соленоида

Рис. 3. Возможные траектории движения электронов в магнетроне
В реальном магнетроне, вследствие разброса скоростей электронов, некоторой неизбежной асимметрии электродов, нарушения соосности катода и магнитного поля, анодный ток спадает до нуля в некотором интервале значений В (см. рис. 3), Iа – анодный ток.
Если бы скорость всех электронов, вылетающих с катода, была одинакова, то с увеличением индукции магнитного поля соленоида анодный ток в лампе изменялся бы в соответствии с пунктирной линией на рис. 4, а.

Рис. 4. Зависимость анодного тока от индукции магнитного поля
соленоида (а) и кусочно-линейная аппроксимация зависимости Ia(Ic) (б)
Реальная зависимость Iа = f(В) изображена на рис. 4, а сплошной линией.
Рассмотрим критический режим. Учитывая, что магнитное поле соосно катоду, т.е. V В, для значения силы Лоренца получим
F = e [V Bкр]. (9)
Если считать, что электроны движутся с постоянной скоростью, то сила Лоренца будет являться центростремительной:
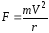 , (10)
, (10)
где r – радиус кривизны траектории электронов.
Электрон, прошедший разность потенциалов, обладает кинетической энергией
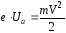 . (11)
. (11)
Решая совместно уравнения (9), (10) и (11), получаем
 . (12)
. (12)
При критическом значении индукции магнитного поля радиус кривизны траектории электронов
r = (a–b)/2, (13)
где а – радиус цилиндрического анода; b – радиус нити катода.
Поскольку нить катода достаточно тонка по сравнению с диаметром цилиндра анода, то радиусом катода можно пренебречь. С учётом этого получаем
r = a/2. (14)
Подставляя (14) в (12), определяем значение e/m:
 . (15)
. (15)
Аксиальное магнитное поле создаётся соленоидом, внутри которого помещается электронная лампа.
Индукция магнитного поля на оси соленоида конечной длины определяется выражением
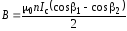 , (16)
, (16)
где n – число витков соленоида на единице длины (n = N / L; N – полное число витков соленоида; L – длина соленоида); Iс – ток соленоида; 1, 2 – углы, под которыми из точки на оси, где определяется индукция, видны радиусы крайних витков соленоида (рис. 5).
Если магнетрон находится в центре соленоида, то

и формула (16) принимает вид
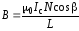 . (17)
. (17)

Рис. 5. Схема расположения углов 1 и 2 в соленоиде
Окончательно, подставляя формулу (17) в (15), получим
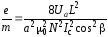 . (18)
. (18)
Принципиальная схема установки изображена на рис. 6.

Рис. 6. Принципиальная схема установки для определения e/m
