§ 14. Энергия в : лектростатике
План
I. энергия глектростатического поля.
II. энергия зарядов, распределенных с объемной и поверхностно!1 плотностью в поле.
ill. "нергия системы точечных зарядов в поле,
1У. энергия диполя в поле.
#1* - нергия системы точечных зарядов: собственная энергия и энергия взаим
действия.
У*. Энергия диполь-дипольного взаимодействия.
УII. Классический радиус электрона.
I. По теореме Умова-Пойнтинга • нергия электромагнитного поля равна:
Г /. Г£^$i Т§р})Л*' Я^Д*1 энергия лектростатического поля:
Формула ^<!.5<!) означает, что энергия поля "размазана" по объему V" с
объемной плотностью YVt-jl}rE£iJ?rO . Вея энергия поля согласно
fe*b'd) всегда положительна. I тот вопрос обсу-дался в § 6.
II. Получим энергию зарядов в поле. Для этого вводим ^иы^^ • Тог-
да, подставив эту формулу в , полним:
J -г*
Qbtyuuflf преСразуем согласно то-.деству ^bjP^HJU? &Н4&*ЦА-
согласно
4-му Уравнению : аксвелла, получим: %fl^^-с/^)-У^. одставив
• то выражение в формулу для энергии и сразу разбивая ВДГдм интеграла,
получаем:
На ртом этапе 1нергия имеет вид: .
Второй интеграл в ^«53)яВКМ| преобразовать по 1*1 теореме Остроградского
Гаусса: р р
Но так '".е, как И в 9 13 , отметим, что применение ; той теоремы возмож-
но только в случае, если нет поверхностей разрыва подинтегральых функций*
'-~-----• Т. v *^ *1
Рассмотрим два возможных случал.
1. Во всем пространстве, занятом полем, нет поверхностей разрываЯ)ли *f
Тогда Ф Цф„ ~> /<<*Х„^ -*0,
г'Де So -Поверхность, охватывающая полное поле, "ри этом WJbrrofS'** О
при *£.-л^о . Сто возможно, если заряды находятся в конечной области
пространства. Подробны?1 анализ аналогичных выражений мы уже проводили
в § 13. Учтем этот результат и получим вместо выражение для
энергии:
2 £»» одна поверхность взрыва нормальной составляющей вектора элект-
рической индукции, на которой выполняете,- граничное условие Q.G7_p :
'АУЛ П — wi — ■ -
Скалярный потенциал терпит разрыв при переходе через двойной электричес-
кий слой ( см, нарример, Й.Е. Таил \ . Но двойные электричес-
кие слои встречаются крайне редко, поэтому в дальнейшем всегда судем
считать }f всюду непрерывным.
Снова, как и в § 13, применим тот же рисунок 22. Тогда запишем:
При этом с интегралом по внешней поверхности S можно поступить, как
в 1-м случае, а именно:
Поэтому остается интеграл по "внутренней" поверхности / t который
приближенно можно записать на в виде суммы двух интегралов - по Sf и S% :
Поскольку (0x4 = —$)fH » так как нормалв /?^и И параллельны,
a — fdjfit так как нормали /?ь и (Г антипараллельны, то
после устремления St ~>$/*лур ■ £t ^^^"bf » получаем:
\У Spay , .
Используем граничное условие (1.67 J и записываем:
1^ 4 ^ ', где снова опущено
■"слово" разрыв" для поверхности, на которой 0* и=МЭд> Подставим этот
результат в (kJ.oS*) и получим:
v-ijjw * (?.«)
Фордгула /£.55^описываецшнергию зарядов, распределенных с объемно!':^ ^ и
поверхностной (плотностью, в электростатическом поле, сто потенциаль-
ная энергия заряженного вещества в поле. Вещество в ^.5^ представлен^
плотностями : арядов у к 0* » а поле - потенциалом V • Формула С3»бб1 ограниченна по сравнение с исходной ) . В самом деле, сог-
ласно ^2»661 энергией обладают только области пространства, в которых нахолится заряженное вещество. А если вещество не заряжено или его вооб- ще нет, то энерги'-согласно (2»5.13^равна нулю ! Тогда как согласно (2,52) энергия есть в тан , где вещества нет, а поле есть ! И последнее замечание. Согласно (29ЪЬ ) энергия зависит от% значения потенциала в некотого" точке, ^то снова подтвешдает точку зрения 2 и £ и автот>а/ - наличие физического смысла потенциала. Потенциал, таким образом, является энергетическо; характеристике;' поля»
ill* ПереГдем теперь к нахождению энергии системы точечных зарядов в поле а/ 11 ока ем, что для точечных зарядов мо>..но ввести понятие объемной плот- ности.
Объемная плотность заряда в самом простом случае / равномерное {ко- предел ение по объекту / равна: » — . J-
I V '
Дм точечного заряда f ведет себя "своеооразно", а именно:
р ^ J о° ; в точке, где находится заряд, так какТ=^^.5б)
) / О во всех остальных точках, так как в них^- о,
Дирак преду* о ил использовать для описания $ дельта-функцш. Дельта-Пункция Дирака:
Г/ 1 f °° > Х = °
Нормировка дельта-пункции - на единицу , т.е. . ЩЫШ =- i i анаЛогично / f(**«W± I .
Ксли под знаком интеграла кроме или J^r-rf ) находится непрерывная
ХУД'™ /Л / 1 т0 ''нтбгр^лы вычисляются очень просто:
лсть функции, которые ведут себя дельта-образно - если они иг/еот острый максимум. Для них мо>но to>v6 использовать fz^9") .
С учетом свойств дельта-функции Дурака можно ввести понятие объемной плот' ности зарядов для системы точечных зарядов: ^ -
где ^ характеризует положение заряда ty* , У/г-Ъь) ' о6об1Дение дельта-функции Дирака на трехмерный случай:
Проверим правильно ли мы ввели / согласно (2.60) Вычислим:
Как и следовало ожидать, получился заряд все£сгстемы зарядов. При втои использовалась нормировка обобщенной дельта-функции Дирака.
Итак, можно формально описывать систему точечных зарядов с помощью объемной плотности, но в конце концов бесконечность все-таки появится !
ОиЬеМНиУ! UAS/rnVVlB, n\j и —--------------
б/ Найдем энергию системы точечных зарядов в поле. Для этого использу- ем формулу для энергии с £ (2.54^ уведенную по (2.60? и свой-
где использовано свойство С2.59) для трехмерного случая:
Интегрирование ведется по всему пространству Итак.
(2.61)
Это потенпиальная энергия системы точечных зарядов в поле. При этом по- ле характеризуется потенциалом *fic в той же точке, в которой находится заряд ^ • Конечно, эта формула так же ограниченна по сравнению с фор- мулой ДЛ) энергии поля.
1У. Найдем "полезную" формулу для энергии диполя во внешнем ncjiemif.l^?
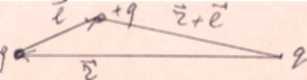
Рис. 23. Диполь во внешнем поле
Б точке ^ находится !. сточиик поля. 11а заряде -"-^ потенциал заряде -f f. потенциалУ/?7^2 нергия этих зарядов в поле:
Разложим yfttfi) в ряд, считая :
и подставим в энергию: ^ ~* ч
Р!так, энергия диполя во внешнем поле:
гта формула используется г- гиэике для описания поведения диэлектриков в электрическом поле.
У. Найдем энергию диполь-дипольного взаимодействия, т.е. энергию двух диполей с моментами Д я . Для этого используем (2.62/ , предпола- гая, что диполь с моментом fa находится в мле диполя с моментом pt • Сначала найдем напряженность поля диполя. Пусть
При этом мы использовали тождество векторного анализа
полагая tf=& и <f=(jg* t) Я (\>> * ^1
й^векторвог» анализа . Отдельно найдем: ^ХАМ( fi-Zj -
-1* j £ * Ф-
так как ft^Xfifo$i>fel я f не зависит от координат
fXr^-l) точки наблюдения.
Тогда напряженность поля диполя равна:
Подставим ('г.бз) в формулу Г2.62 % получимrJ ^
2.
у= г* \г ' (а,
Это и есть энергия диполь-дипольного взаимодействия. У1 . Находим энергию системы точечных зарядов. Для этого используем формулу fe.6i? , считая , что потенпиал ^ на заряде создается той же системой точечных зарядов. Для выделенной пары зарядов(см. Рис.24): .Ji j
Тогда ■
В
-нергия всех зарядов получится в виде:
тих суммах можно выделить отдельно суммы при ^ и /*^f- if : Г ^ ^/й':№«1 2- ****/Г*<ч1 6.66 j
rgjfW$&£*g ^Г^ц Ft*" ?4 - собственная энергия системы точечных зарядов. Она, как видно, бесконечна. Вот бесконечность и "вылезла", хотя мы в начале "запрятали" ее в ,чях? объемную плотность ^> .
Второй член в /2.65) гавен конечному значению;
iro энергия взаимодействия. Причем, МП W&»>0 , то заряда от- талкиваются - одноименные, если Л q » ™ заряда притя- гиваются, -
В обгсем согласно энергия системы точечных зарядов бесконечна,
но в ней есть конечное значение - энергия взаимодействия.
УЛ. Классический радиус электрона.
В современной теоретической физике существует проблема, связанная с энергией элементарных частиц. Наименьшей частицей вещества является г-лектррн. Поскольку глектрон заряжен, то его собственная энергия Vt/'4'^' , где й - радиус электрона. Можно непосредственными вычисле- ниям!^" ^см. Приложение Jf показать, что собственная глектростатичес-
кая энергия шара, равномерно заряженного по объему.равна:
С • J
Если электрон - точечная частица, то его собственная энергия бесконечна, так как &-*0 . Однако согласно СТО к специальная теория относительно- сти D энергия Ц/=- Мс С | где }rto ~ масса покоя электрона, ота энер- гия конечна I Следовательно, возникает противоречие электродинамики и СТО.
Если электрон - протяженная частица радиуса Q, , то его собственая электростатическая энергия конечна согласно , например, Q2.67J . Но сно- ва возникает противоречие с СТО. Формула (Х.бЧ) получается в предполо- жении, что шарик -электрон - абсолютно твердое тело, но согласно СТО таких тел Сыть не может, иначе это означало бы передачу взаимодействия с бесконечной скоростью. А согласно СТО предельной скоростью физического взаимодействия является С - скорость света в вакууме, необходимо от- метить, чтв проблема взаимодействия элвмх протяженных элементарных час- тиц до сих пор не решена.
Чтобы "примирить" электродинамику с СТО, в настоящее время предпола- гают, что элементарные частицы, в том числе электрон, точечные, но это не радиус частицы, а нижняя граница применимости электродинамики, на которой она еще не противоречит СТО. <1та нижняя граница получила наз- вание "классический радиус электрона", хотя никаким радиусом электрона не является. Находится классический радиус следующим образом: предполар гаетс.г равенство энергий ■ лектростатической и энергии поко^ электрона:
'де ^ - классический радиус электрона, равный Qt~*i ' СЛ4-
§ 15. Механические силы в электростатике. ~*
Из определения вектора рлектркпеско? напрлтенкостк t слезет, что для точечного заряда сила равна:
(J2.69)
#Если заряд распределен по объему с плотностью Ф , то можно, вищоляя при- меняя ^2.69^ к элементу объема<AV с зарядом записать:
где j^pB - объемная плотность силы. В итоге, сила, действующая на объем \Г , равна: р гг
В случае поверхностного распределения зарядов с плотностью о дело несколько усложняется, так как на поверхности d§ в силу граничных усло- вий вектор £" неопределен.
Дл^ одного уединенного проводника возникает эффект растяжения его поверхности, сто объясняется тем, что элементы поверхности заряжены одно- именномМотталкиваются, но покинуть проводник не могут.
Для проводика, помещенного во внешнее поле, возникает аналогичный эф- фект. В самом деле, выберем элемент поверхности проводника dS » набо- ром находятся заряды с плотностю (3-WS ( ?U£ 25 J . Внешнее поле вблизи поверхности d$ направлено по нормали Тг (дм, § 12 ) , поле £г' от заряда <Г*с(§ направлено вверх и вниз, поле £п - от всех осталь- ных элементов поверхности направлено вверх. Все эти векторы, находятся конечно, вблизи cf$ ив одно!'уточке.
Рис.25. Провод^во нешнем поле. "F1 этом V r*j? и e^G'+e"-* вне проводника
£Г = С-Р^ б? внутри проводника
Отсюда
Тогда сила, действующая на фпеыент cl£ :
где "btut^ixi*1* tr5*
при этом -$п*( = «мг * " ST0 поверхностнал^плот1 гость механическ* ких сил, равная осъемно. плотности электростатической) энергии поля. Она действует по Hopi/али к каждому элементу ct$ • Тогда вся сила может быть ■аписаяа: ~* С / _0 /
Наедем силу, де^ств^^уп на диполь в поле^. Согласно Рис.<;6 в точке, где находится заряд -~f иапря?.енн^ть_полм , в точке, где нахо-
дите заряд т*-£ шрлмнрост c/^j, Находим результирутптую силу:
Рис.^б. Диполь во внешнем поле. Разло Bf't'f-t) I raj,
Подставим это разло- енне в силу г и получаем: "так, сила, действующая ка диполь, равна:
где оператор fr-Pj = f*Vc '
Согласно сила действует на диполь в неоднородно?/; поле в стогону
увелгченда (: . В од1:ородиом поле сила F равна нулю, но действует момент пары сил F4 - , численно равных, но направленных в разные
стороны. В ежим этот момент.1 , р? 7 т-Zp У\л£7 -
Момент N стремится повернуть диполь так, что(Лг/? совпадало с & . .
Совместным действием момента N и силы объясняется притяжение лег- ких тел /бумаяек, пылинок и т.п / к наэлектризованным телам. Зтим объяс- няются эффектные опыты, которые демонстрирует школьный учитель в самом начале преподавания раздела "электростатика".