
- •Введение
- •Глава I. Оchobы макроскопической электродинамики
- •§I. Четвертое уравнение Максвелла как обобщение экспериментального закона Кулона
- •1) Сначала отвлечемся от точки 2 и напишем формулу для любой точки поля: ,
- •§ 5. Система уравнений Максвелла
- •§ 6. Закон сохранения и превращения энергии электромагнитного поля. Теорема Умова-Пойнтинга.
- •§ 7. Граничные условия для нормальных и касательных составляющих векторов электромагнитного поля
- •Глава 11. Электростатика
- •§ 8. Основные уравнения. Основные задачи электростатики
- •§ 9. Основные свойства поля. Скалярный потенциал, его связь с работой.
- •§10. Дифференциальные уравнения для потенциала, их общие решения. Нормировка потенциала. Решение 2-й задачи.
- •§ 11. Разложение потенциала системы зарядов на больших расстояниях,
- •§ 12. Проводник в электростатическом поле
- •§ 13. Диэлектрики в электростатическом поле
- •§ 14. Энергия в : лектростатике
Глава 11. Электростатика
§ 8. Основные уравнения. Основные задачи электростатики
Электростатика
– раздел электродинамики, изучающий
поле неподвижных электрических зарядов.
Но электрические заряды неподвижны
только в одной инерциальной системе
отсчета (ИСО). Во всех других ИСО они
движутся. Следовательно, все результаты
электростатики применимы только к этой
одной ИСО. Поскольку заряды неподвижны,
 Из уравнения непрерывности (1.40) так как
Из уравнения непрерывности (1.40) так как
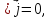 следует
следует
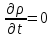 ,
и
,
и
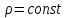 .
Кроме
того, в статике
.
Кроме
того, в статике
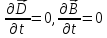 .
Тогда
уравнения Максвелла (см. §5) примут вид:
.
Тогда
уравнения Максвелла (см. §5) примут вид:
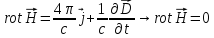
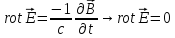
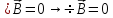
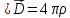
 .
.
Эта система уравнений разбивается на две подсистемы, не связанные друг с другом – на электрическую и магнитную:
Электрическая

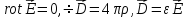
Магнитная
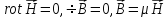
Решение
для магнитной системы с учетом граничных
условий – тривиальное, т.е.
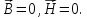 Это
означает, что в данной ИСО магнитная
компонента электромагнитного поля
отсутствует. Однако электрическая
компонента есть
Это
означает, что в данной ИСО магнитная
компонента электромагнитного поля
отсутствует. Однако электрическая
компонента есть
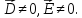 Это
и есть электростатическое поле. Оно
описывается уравнениями электрической
подсистемы. Следовательно, основные
уравнения электростатики:
Это
и есть электростатическое поле. Оно
описывается уравнениями электрической
подсистемы. Следовательно, основные
уравнения электростатики:
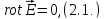
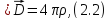
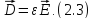
Основные задачи электростатики:
1)
Прямая
задача
– по
 найти
найти
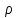 и
и
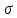 .
.
Решение находим из 4-го уравнения Максвелла (2.2):
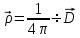
И граничного условия (1.67)
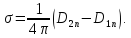
2)
Обратная задача - по
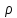 и
и
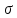 найти
найти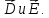 Решается
интегрированием (см. § 10).
Решается
интегрированием (см. § 10).
3) Найти механические силы, действующие на заряженные тела в электростатическом поле.
§ 9. Основные свойства поля. Скалярный потенциал, его связь с работой.
Уравнение
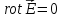 означает,
что электростатическое поле безвихревое,
имеет незамкнутые силовые линии, связано
с зарядами. Силовые линии начинаются
на положительных зарядах и кончаются
на отрицательных.
означает,
что электростатическое поле безвихревое,
имеет незамкнутые силовые линии, связано
с зарядами. Силовые линии начинаются
на положительных зарядах и кончаются
на отрицательных.
Основные свойства поля обусловлены его безвихревым характером. Рассмотрим эти свойства.
1) Вычислим работу по перемещению заряда по замкнутому контуру, используя уравнение (2.1) и теорему Стокса:

Итак,
работа по замкнутому контуру равна
нулю:
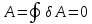
2)
Покажем, что работа, совершаемая по
перемещению заряда между двумя точками
поля, не зависит от формы пути. На рисунке
16 это точки
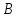 и
D.
Указаны
два разных пути – через точку
K
и
через точку
M.
и
D.
Указаны
два разных пути – через точку
K
и
через точку
M.
Требуется доказать, что работа в этом случае одинакова:

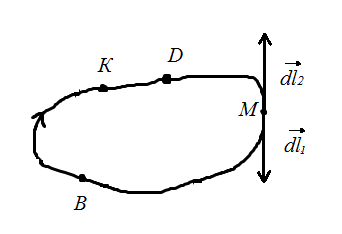 Рис.
16 Замкнутый путь
Рис.
16 Замкнутый путь
Докажем это свойство, используя только что доказанное №1.
Согласно
свойству 1 работа по замкнутому контуру
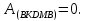 Ее
можно разбить на работу из точки
Ее
можно разбить на работу из точки
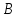 через
через
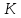 в
точку
в
точку
 и
из точки
и
из точки
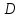 через
точку
через
точку
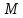 в
в
 :
:
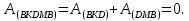
Отсюда
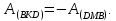
Но работа
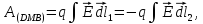
т.к.
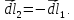 (см.
рис. 16)
(см.
рис. 16)
А это работа
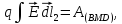
следовательно
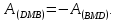
Рассматривая совместно (2.4) и (2.5) получаем
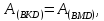
что и требовалось доказать.
Итак, работа, совершаемая по перемещению заряда между двумя точками поля, не зависит от формы пути. Необходимо выяснить, от чего, от какой величины она зависит.
3)
Сначала снова используем уравнение
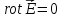 и тождество векторного
анализа
и тождество векторного
анализа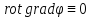 .
Уравнение
(2.1) удовлетворяется, как видим,
если
положить:
.
Уравнение
(2.1) удовлетворяется, как видим,
если
положить:
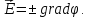
Выберем
знак. Для положительного точечного
заряда согласно определениям
вектора
 и градиента скаляра
и градиента скаляра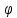 имеем в точке М (см. Рис.17)
имеем в точке М (см. Рис.17)
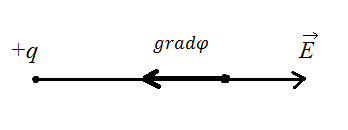 Рис.
17
Рис.
17
Поэтому в дальнейшем е электродинамике всегда полагают:
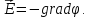 (2.6)
(2.6)
Это
основная формула, связывающая вектор
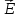 и скаляр
и скаляр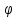 .
Необходимо выяснить, что собой представляет
введенный таким образом скаляр
.
Необходимо выяснить, что собой представляет
введенный таким образом скаляр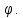
4)
Для этого найдем элементарную работу,
т.е. работу, совершаемую по перемещению
единичного положительного заряда на
бесконечно малом пути
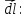
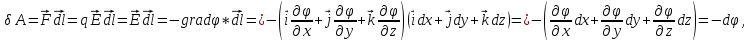
при
этом использовались выражения для
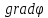 и
и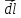 в
декартовых
координатах.
в
декартовых
координатах.
Итак,
 (2.7)
(2.7)
Формула
(2.7) означает, что в безвихревом поле
элементарная работа
по перемещению
единичного положительного заряда –
есть полный дифференциал введенного
нами скаляра
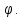
5) Найдем, наконец, работу между двумя точками поля, например, точками 1 и 2:
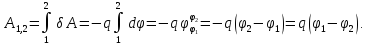
Итак,
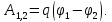 (2.8)
(2.8)
Согласно
(2.8) работа зависит от разности значений
скаляра
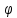 в начале
и конце пути. Следствия 4) и
5) показывают, что скаляр
в начале
и конце пути. Следствия 4) и
5) показывают, что скаляр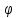 характеризует
способность поля
совершать работу. Поэтому
характеризует
способность поля
совершать работу. Поэтому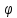 называется скалярным потенциалом поля
или просто потенциалом.
называется скалярным потенциалом поля
или просто потенциалом.
В
некоторых случаях, если в бесконечности
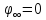 ,
можно
получить
простое определение потенциала.
Пусть в формуле (2.8) вторая точка находится
в бесконечности. Тогда
,
можно
получить
простое определение потенциала.
Пусть в формуле (2.8) вторая точка находится
в бесконечности. Тогда
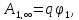 откуда
откуда
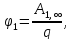
Если
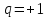 ,
то
,
то
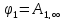 (2.9)
(2.9)
Это
означает, что потенциал можно определить
как работу, совершаемую
полем по
перемещению единичного положительного
заряда из данной точки
в бесконечность.
Подчеркнем, что такое определение
возможно лишь в предположении, что в
бесконечности
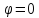 .
Реально это соответствует случаям,
когда
заряженные объекты занимают конечную
область пространства. В этом
случае
потенциал с увеличением расстояния
убывает и можно положить,
что в
бесконечности он обращается в нуль.
.
Реально это соответствует случаям,
когда
заряженные объекты занимают конечную
область пространства. В этом
случае
потенциал с увеличением расстояния
убывает и можно положить,
что в
бесконечности он обращается в нуль.
