
- •Введение
- •Глава I. Оchobы макроскопической электродинамики
- •§I. Четвертое уравнение Максвелла как обобщение экспериментального закона Кулона
- •1) Сначала отвлечемся от точки 2 и напишем формулу для любой точки поля: ,
- •§ 5. Система уравнений Максвелла
- •§ 6. Закон сохранения и превращения энергии электромагнитного поля. Теорема Умова-Пойнтинга.
- •§ 7. Граничные условия для нормальных и касательных составляющих векторов электромагнитного поля
- •Глава 11. Электростатика
- •§ 8. Основные уравнения. Основные задачи электростатики
- •§ 9. Основные свойства поля. Скалярный потенциал, его связь с работой.
- •§10. Дифференциальные уравнения для потенциала, их общие решения. Нормировка потенциала. Решение 2-й задачи.
- •§ 11. Разложение потенциала системы зарядов на больших расстояниях,
- •§ 12. Проводник в электростатическом поле
- •§ 13. Диэлектрики в электростатическом поле
- •§ 14. Энергия в : лектростатике
§10. Дифференциальные уравнения для потенциала, их общие решения. Нормировка потенциала. Решение 2-й задачи.
Найдем дифференциальные уравнения для потенциала. Для этого запишем 4-е уравнение Максвелла и уравнение связи:
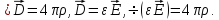
Используем тождество векторного анализа
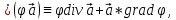
при
этом полагая
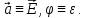
Тогда
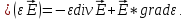
Подставим
вместо
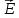 из (2.6) выражение для
из (2.6) выражение для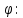
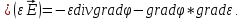
Согласно векторному анализу
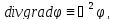
Тогда
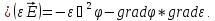
С
учетом этих преобразований вместо 4-го
уравнения Максвелла получаем уравнение
для
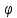 :
:
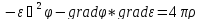
Или
разделив обе части уравнения на
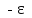 ,
получим:
,
получим:
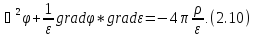
Это
дифференциальное уравнение для
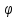 в
неоднородной среде. Стандартного решения
оно не имеет.
в
неоднородной среде. Стандартного решения
оно не имеет.
Для
однородной среды
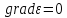 .
Тогда вместо уравнения (2.10)
получаем:
.
Тогда вместо уравнения (2.10)
получаем:
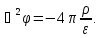

Это
уравнение Пуассона для потенциала
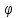 .
.
Если
 ,
то получается уравнение Лапласа:
,
то получается уравнение Лапласа:
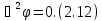
Уравнение Лапласа – однородное дифференциальное уравнение 2-го порядка в частных производных. Оно описывает потенциал поля вне заряженного тела в однородной среде. Общее решение уравнения:
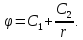
Постоянную
интегрирования
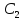 можно выбрать в виде
можно выбрать в виде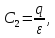 где
где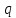 – заряд
тела (см. Приложение III).
Тогда:
– заряд
тела (см. Приложение III).
Тогда:
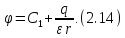
Постоянную
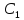 определим из условия нормировки.
Нормировка потенциала – процедура
придания однозначности потенциалу.
Иначе говоря, выбор определенного
значения
определим из условия нормировки.
Нормировка потенциала – процедура
придания однозначности потенциалу.
Иначе говоря, выбор определенного
значения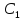 ,
так
как согласно (2.13) и (2.14)
,
так
как согласно (2.13) и (2.14)
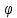 определяется неоднозначно.
определяется неоднозначно.
Как
видно из решений (2.13) и (2.14) ,
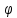 убывает с ростом
убывает с ростом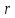 .
Вполне
.
Вполне
разумно
потребовать, чтобы в бесконечности
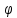 обращался в нуль;
если
обращался в нуль;
если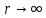 ,
то
,
то
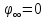 .
Тогда для бесконечности имеем:
.
Тогда для бесконечности имеем:
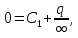
откуда
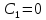 .
.
После нормировки общее решение запишется так:
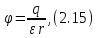
Формально оно совпадает с потенциалом поля точечного заряда, известного из курса общей физики.
Решение
уравнения Пуассона найдем не строго,
чисто качественно.
Для этого разбиваем
весь объем
 ,
заряженный с объемной плотностью
,
заряженный с объемной плотностью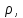 на элементарные объемы
на элементарные объемы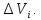 Причем
Причем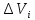 имеет заряд
имеет заряд такой,
чтобы его можно было считать точечным.
такой,
чтобы его можно было считать точечным.
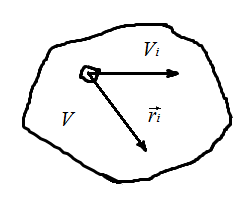 Рис.
18 Объем
Рис.
18 Объем
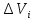
Тогда
можно применить полученное решение
(2.15) для
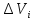 :
:
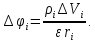
Потенциал
от всех элементов
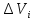 объема
объема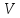 находим по принципу суперпозции:
находим по принципу суперпозции:
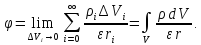
Итак,

Это и есть искомое решение уравнения Пуассона, строго оно получается в курсе "методы математической физики".
Решения
(2.15) и (2.16) отличаются при
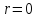 .
В
самом деле, согласно (2.15)
.
В
самом деле, согласно (2.15)
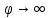 при
при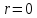 .
Это означает, что применять решение
(2.15) при
.
Это означает, что применять решение
(2.15) при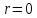 нельзя, нарушается требование точечности
заряда.
нельзя, нарушается требование точечности
заряда.
Решение
(2.16) не расходится при
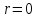 .
Рассмотрим решение для
.
Рассмотрим решение для :
:
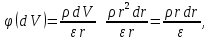
Если
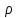 не уменьшается с уменьшением
не уменьшается с уменьшением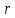 .
.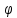 при этом может обращаться в нуль, либо
быть постоянным. Так что (2.16) является
более общим решением.
при этом может обращаться в нуль, либо
быть постоянным. Так что (2.16) является
более общим решением.
В электродинамике дискутируется проблема, обусловленная неоднозначностью потенциала, существует две точки зрения:
1)
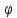 неоднозначен и поэтому является
вспомогательной функцией, никакого
неоднозначен и поэтому является
вспомогательной функцией, никакого
физического смысла не имеет.
2)
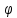 неоднозначен, но можно придать ему
однозначность и физический смысл
неоднозначен, но можно придать ему
однозначность и физический смысл
Автор придерживается второй точки зрения.
Отметим, что неоднозначность потенциала не влияет на значение напряженности и работы. В самом деле:
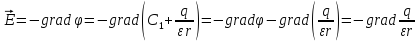 ,
,
т.к.
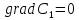
Аналогично для работы находим:
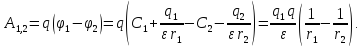
Напряженность и работа имеют одно вполне определенное значение.
К этой проблеме мы будем возвращаться скова в последующих главах.
Теперь учтем все возможные случаи распределения заряда и запишем потенциал:

Тогда электрическая напряженность равна:
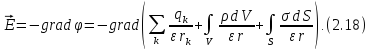
Это и есть решение 2-й задачи электростатики в общем виде.
