
- •Л.А. Внукова, о.А. Дерябина, н.Н. Егорова, е.В. Селезнева основы информатики
- •Оглавление
- •Введение
- •Раздел 1. Представление числовой информации
- •1.1. Понятие о системах счисления. Основные определения
- •1.2. Представление чисел в позиционных системах счисления
- •1.3. Перевод десятичных чисел в другие системы счисления и обратно Перевод целых чисел
- •Перевод дробных чисел
- •Перевод смешанных чисел
- •1.4. Арифметические операции в позиционных
- •Практические задания
- •Самостоятельная работа Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Раздел 2. Измерение информации
- •2.1. Основные сведения
- •2.2. Алфавитный подход к измерению информации
- •Практические задания
- •2.3. Содержательный подход к измерению информации
- •Практические задания
- •2.4. Вероятностный подход к измерению информации
- •Практические задания
- •Самостоятельная работа Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Раздел 3. Основы логики и логические основы компьютера
- •3.1. Алгебра высказываний. Логические выражения и таблицы истинности Конъюнкция (логическое умножение)
- •Дизъюнкция (логическое сложение)
- •Инверсия (логическое отрицание)
- •Операция логического следования (импликация)
- •Операция логического равенства (эквивалентность)
- •Операция «исключающая или» или «сложение по mod 2»
- •Практические задания
- •3.2. Логические формулы
- •Практические задания
- •3.3. Логические схемы
- •Практические задания
- •Самостоятельная работа
- •4.2. Свойства алгоритмов
- •4.3. Формы записи алгоритмов
- •Словесный способ записи алгоритмов
- •Графический способ записи алгоритмов
- •Программный способ записи алгоритмов
- •Псевдокоды
- •Алгоритмический язык для записи алгоритмов
- •Общий вид алгоритма
- •Команды школьного ая
- •4.4. Компоненты алгоритмического языка
- •Понятия, используемые в алгоритмическом языке
- •4.5. Стандартные функции
- •Арифметические выражения
- •Логические выражения
- •4.6. Основные типы алгоритмических структур
- •Алгоритмическая структура «Следование»
- •Алгоритмическая структура «Ветвление»
- •Алгоритмическая структура «Выбор»
- •Алгоритмическая структура «Цикл»
- •Практические задания
- •Самостоятельная работа
- •Основы информатики
- •644099, Омск, ул. П. Некрасова, 10
- •644099, Омск, ул. П. Некрасова, 10
Практические задания
Постройте таблицы истинности логических функций:
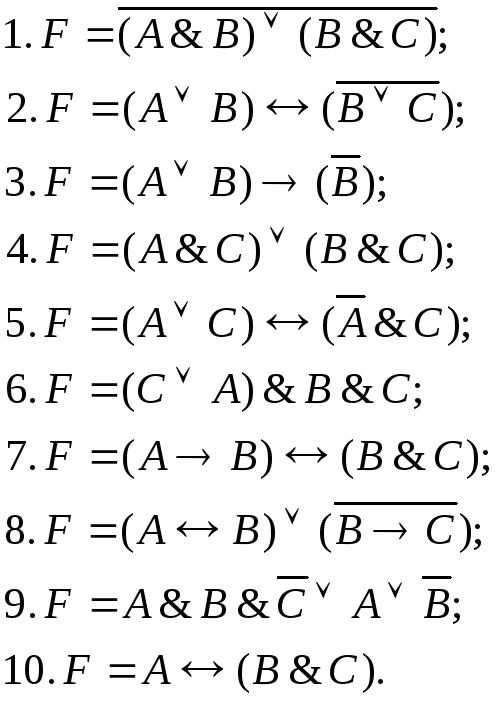
3.2. Логические формулы

Приведем примеры применения перечисленных выше формул.
Пример 1.
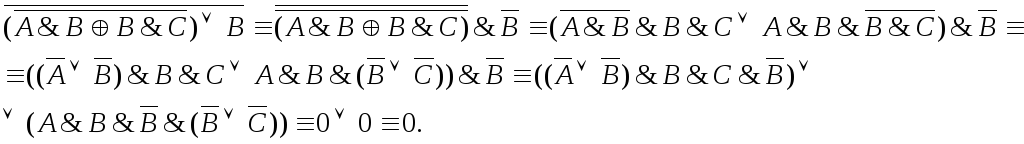
Пример 2.
![]() .
.
Пример 3.
![]()
Практические задания
Упростите логические выражения:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
3.3. Логические схемы
Л огические
схемы могут быть представлены в различной
форме, например:
огические
схемы могут быть представлены в различной
форме, например:
Структурная
формула для данной переключательной
схемы имеет вид
![]() .
.
Комбинационная схема устройства может быть представлена с помощью базовых элементов логических операций.
Базовые элементы логических схем имеют следующий вид:
Дизъюнкция Конъюнкция Импликация

Эквивалентность Сложение по mod 2 Отрицание

Пример. Дана логическая схема. Постройте соответствующее ей логическое выражение.
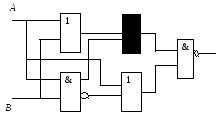
Структурная формула для данной схемы имеет вид
![]() .
.
Практические задания
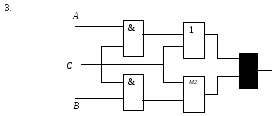
Определите структурную формулу для данных логических схем:

1.

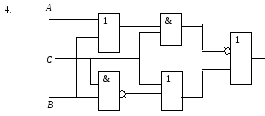
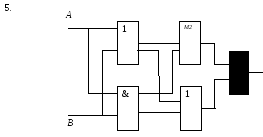
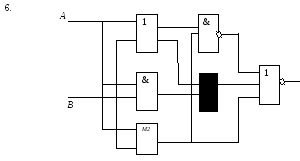
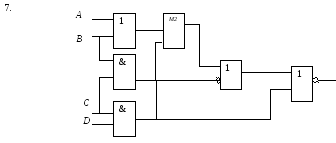
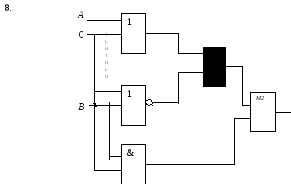
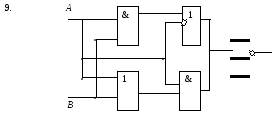
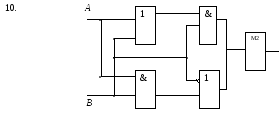
Самостоятельная работа
Вариант 1
Постройте таблицы истинности логических функций:
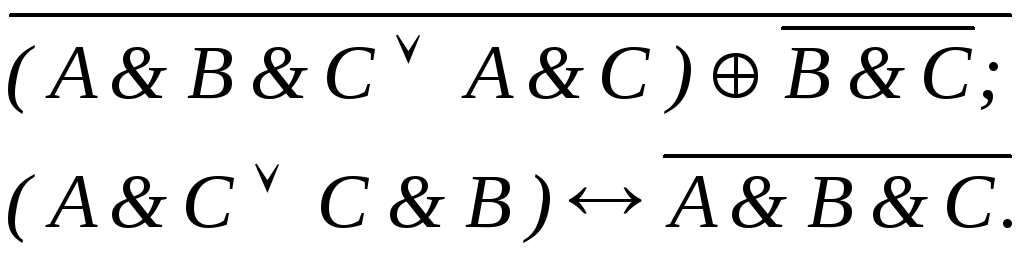
Определите структурную формулу для данных логических схем:
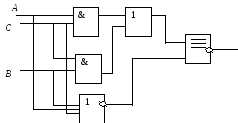
Упростите логические выражения:
![]()
Вариант 2
Постройте таблицы истинности логических функций:
![]()
Определите структурную формулу для данных логических схем:

Упростите логические выражения:
![]()
Вариант 3
Постройте таблицы истинности логических функций:
![]()
Определите структурную формулу для данных логических схем:
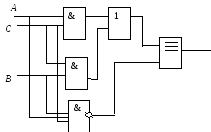
Упростите логические выражения:
![]()
Вариант 4
Постройте таблицы истинности логических функций:
![]()
Определите структурную формулу для данных логических схем:
А & 1




C




M2





& В











&






Упростите логические выражения:
![]()
Вариант 5
Постройте таблицы истинности логических функций:
![]()
Определите структурную формулу для данных логических схем:
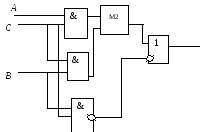
Упростите логические выражения:
![]()
Вариант 6
Постройте таблицы истинности логических функций:
![]()
Определите структурную формулу для данных логических схем:
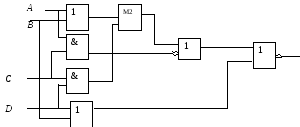
Упростите логические выражения:
![]()
Вариант 7
Постройте таблицы истинности логических функций:
![]()
![]()
Определите структурную формулу для данных логических схем:
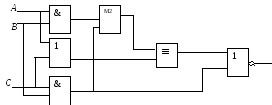
Упростите логические выражения:
![]()
Вариант 8
Постройте таблицы истинности логических функций:
![]()
![]()
Определите структурную формулу для данных логических схем:

Упростите логические выражения:
![]()
Вариант 9
П
остройте таблицы истинности логических функций: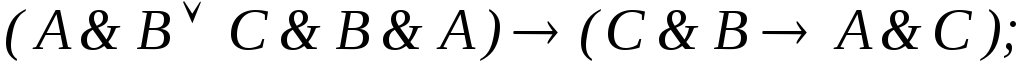
![]()
Определите структурную формулу для данных логических схем:

Упростите логические выражения:
![]()
Вариант 10
Постройте таблицы истинности логических функций:
![]()
![]()
Определите структурную формулу для данных логических схем:
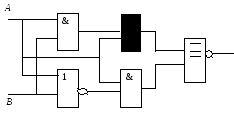
Упростите логические выражения:
![]()
Раздел 4. ОСНОВЫ АЛГОРИТМИЗАЦИИ
4.1. Алгоритм и его свойства
Алгоритмы могут описывать процессы преобразований самых разных объектов. Алгоритм – одно из основных понятий информатики и математики. Само слово «алгоритм» происходит от algorithmi – латинской формы написания имени выдающегося математика IX века аль-Хорезми, который сформулировал правила выполнения арифметических операций.
Алгоритм – это строго детерминированная последовательность действий, описывающая процесс преобразования объекта из начального состояния в конечное, записанная с помощью понятных исполнителю команд.
Для того чтобы изменить состояние объекта, необходимо выполнить над ним определенную последовательность действий. Выполняющий такие операции объект называется исполнителем.
Исполнитель алгоритма– это некоторая абстрактная или реальная (техническая, биологическая или биотехническая) система, способная выполнить действия, предписываемые алгоритмом.
Исполнителя характеризуют:
среда;
элементарные действия;
система команд;
отказы.
Среда (или обстановка) – это «место обитания» исполнителя.
Например, для шахматной фигуры среда – это шахматное поле. Закрашенные клетки – тоже часть среды, а их расположение и положение фигуры задают конкретное состояние среды.
Каждый исполнитель может выполнять команды только из некоторого строго заданного списка – системы команд исполнителя. Для каждой команды должны быть заданы условия применимости (в каких состояниях среды может быть выполнена команда) и описаны результаты выполнения команды.
После вызова команды исполнитель совершает соответствующее элементарное действие.
Отказы исполнителя возникают, если команда вызывается при недопустимом для неё состоянии среды.
Обычно исполнитель ничего не знает о цели алгоритма. Он просто выполняет все полученные им команды.
В информатике универсальным исполнителем алгоритма является компьютер.
