Инверсия (логическое отрицание)

Присоединение частицы НЕ к высказыванию называется операцией логического отрицания или инверсией.

Обозначение отрицания логического высказывания А: или.

Истинность высказывания F=для логического высказыванияА задается следующей таблицей:

А	F=
0	1
1	0

Операция логического следования (импликация)

Логическое следование (импликация) образуется соединением двух высказываний в одно с помощью оборота речи «если…, то…».

Логическая операция импликация «если А, то В» обозначается .

Составное высказывание, образованное с помощью операции логического следования (импликации), ложно тогда и только тогда, когда из истинной предпосылки (первое высказывание) следует ложное высказывание.

Таблица истинности составного высказывания F=имеет вид

А	В	F= A B
0	0	1
0	1	1
1	0	0
1	1	1

Операция логического равенства (эквивалентность)

Логическое равенство (эквивалентность) образуется соединением двух высказываний в одно с помощью оборота речи «… тогда и только тогда, когда…».

Логическая операция эквивалентность « А тогда и только тогда, когда В» обозначается .

Составное высказывание, образованное с помощью операции логического равенства (эквивалентность), ложно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны.

Таблица истинности составного высказывания F=имеет вид

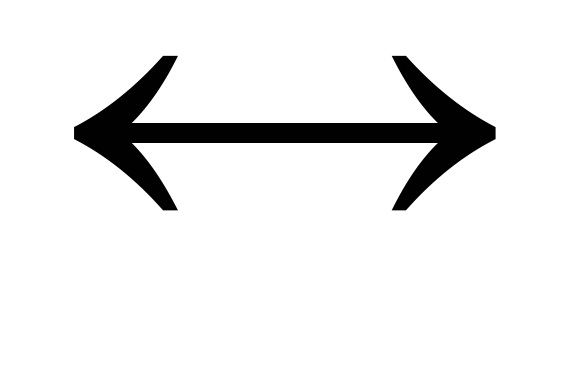А	В	F= A B
0	0	1
0	1	0
1	0	0
1	1	1

Операция «исключающая или» или «сложение по mod 2»

Логическая операция «исключающая или» обозначается .

Составное высказывание, образованное с помощью операции «исключающее или» истинно тогда и только тогда, когда одно из высказываний истинно.

Таблица истинности составного высказывания F=имеет вид

А	В	A B
0	0	0
0	1	1
1	0	1
1	1	0

Теперь на основе полученных логических выражений можно построить из базовых логических элементов схему сложения одноразрядных двоичных чисел.

Пример 1. Постройте таблицу истинности логической функции F=.

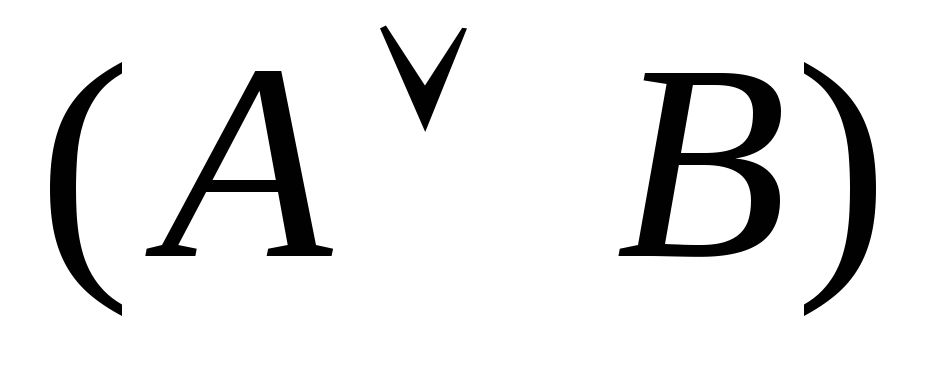
А	В	С			F
1	1	1	1	0	0
1	1	0	1	1	1
1	0	1	1	0	0
1	0	0	1	1	1
0	1	1	1	0	0
0	1	0	1	1	1
0	0	1	0	0	0
0	0	0	0	1	0

Пример 2. Постройте таблицу истинности логической функции

F=.

А	В	С	A&C		B&C	F
1	1	1	1	0	1	1
1	1	0	0	1	0	1
1	0	1	1	0	0	0
1	0	0	0	1	0	1
0	1	1	0	1	1	1
0	1	0	0	1	0	1
0	0	1	0	1	0	1
0	0	0	0	1	0	1

Пример 3. Постройте таблицу истинности логической функции

F=.

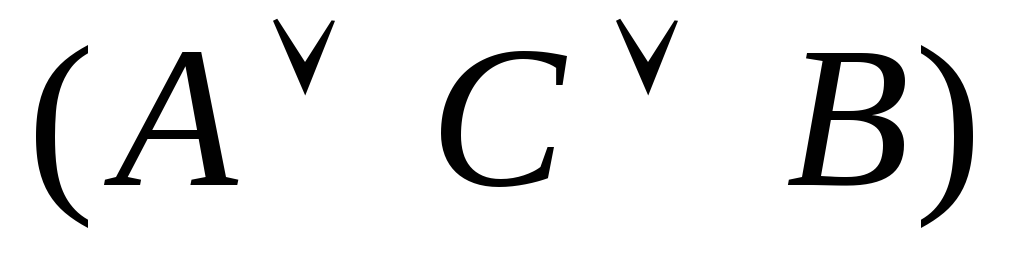
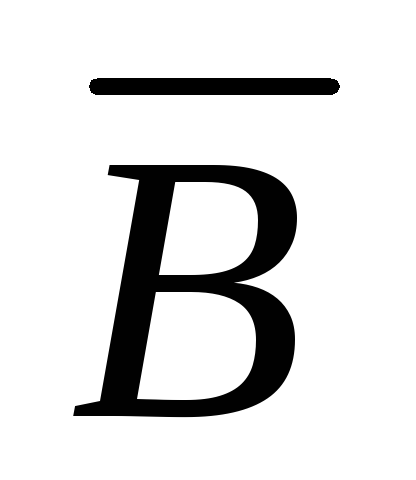
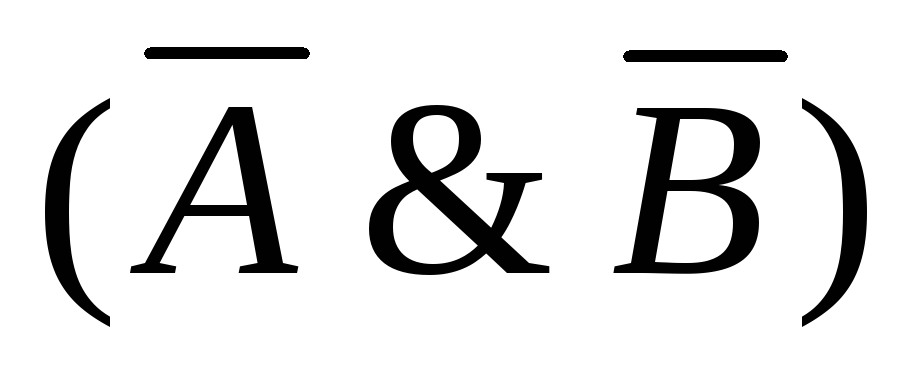
А	В	С					F
1	1	1	1	0	0	0	0
1	1	0	1	0	0	0	0
1	0	1	1	0	1	0	0
1	0	0	1	0	1	0	0
0	1	1	1	1	0	0	0
0	1	0	1	1	0	0	0
0	0	1	1	1	1	1	1
0	0	0	0	1	1	1	1

Пример 4. Постройте таблицу истинности логической функции

F=.

А	В	С				F
1	1	1	1	0	1	0
1	1	0	1	0	0	1
1	0	1	1	0	0	1
1	0	0	1	0	0	1
0	1	1	1	0	1	0
0	1	0	1	0	0	1
0	0	1	0	1	0	0
0	0	0	0	1	0	0