Корреляционная связь, ее характер и формы

При изучении социально-экономических явлений с ярко выраженной причинно-следственной связью особый интерес для статистики представляют корреляционные связи.

Корреляционная связь неполная, так как заданным значениям факторного (независимого) признака (x) соответствует несколько значений результативного (зависимого) признака (у). Это объясняется тем, что на (у), кроме (х) влияют и другие факторы. Характер корреляционной связи проявляется в изменении среднего значения результативного признака, по мере изменения факторного Особенность корреляционной связи в том, что она является необратимой: (х) влияет на (у), а не наоборот.

По направлению корреляционные связи подразделяются на прямые и обратные.

По аналитическому выражению они могут быть линейными и нелинейными.

При линейной зависимости с возрастанием факторного признака происходит равномерное возрастание или убывание результативного признака. Математически такая связь описывается уравнением прямой, а геометрически – прямой линией.

При нелинейных связях с возрастанием величины факторного признака изменение размера результативного признака происходит неравномерно. Математически такие связи описываются уравнениями гиперболы, параболы и др. нелинейных функций. Геометрически они представляются соответствующими кривыми.

По количеству факторов, действующих на результативный признак, различают однофакторные или парные связи и многофакторные или множественные связи. Наиболее разработанной в теории статистики является методология парной корреляции. Двухмерная модель лежит в основе изучения множественных связей.

Корреляционная связь изучается методами регрессии и корреляции:

• задача регрессионного анализа сводится к выявлению и аналитическому выражению направления и формы связи;

• задача корреляционного анализа заключается в измерении тесноты связи между варьирующими признаками.

Уравнение регрессии, его обоснование и расчет параметров

Математической моделью парной связи является уравнение регрессии. Его теоретическое обоснование производится разными способами:

• логически – осмыслением возможности существования именно данной формы зависимости. Например, связь между осадками и урожайностью связи может быть описана только уравнением параболы второго порядка, т.к. с ростом осадков урожайность возрастает до определенного предела, при дальнейшем увеличении осадков урожайность снижается;

• эмпирически – перебором и оценкой разных типов функций;

• путем использования опыта предыдущих аналогичных исследований.

Решение уравнения регрессии заключается в определении его параметров. Рассмотрим методику расчета на примере линейного уравнения вида:

где – теоретические значения результативного признака – переменная средняя (читается как игрек, в среднем зависящий от икс, или коротко игрек от икс);

а₀, а₁ – параметры уравнения регрессии.

Поскольку (а₀) является средним значением (у) при (х = 0), то экономическая интерпретация его часто затруднена или невозможна.

Параметр (а₁) – коэффициент регрессии показывает, на сколько единиц в среднем изменяется результативный признак с изменением факторного признака на единицу. Отрицательный знак показателя говорит об обратной связи, положительный – о прямой связи.

Для удобства интерпретации параметра (а₁) используют коэффициент эластичности (Э). Он показывает, на сколько процентов, в среднем, изменяется результативный признак при изменении факторного признака на 1% и вычисляется по формуле:

Для нахождения параметров уравнения регрессии применяется метод наименьших квадратов. Суть метода в том, что сумма квадратов отклонений фактических значений (у) от выровненных должна быть минимальной:

Для этого частные производные данной функции приравниваются к нулю:

откуда получается система нормальных уравнений:

где n – число единиц наблюдения.

Для нахождения параметров можно использовать также следующие формулы:

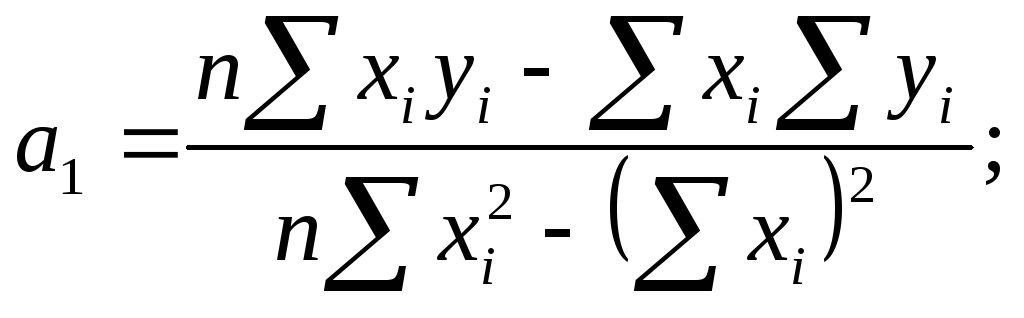
Подставив числовые значения параметров (a₀) и (a₁) в исходное уравнение, находим значения, зависящие только от заданных(х).