12.3. Числовые ряды с комплексными членами

Пусть и– числовые последовательности,– мнимая единица, тогда– последовательность комплексных чисел, если.

Рассмотрим числовой ряд с комплексными членами

.

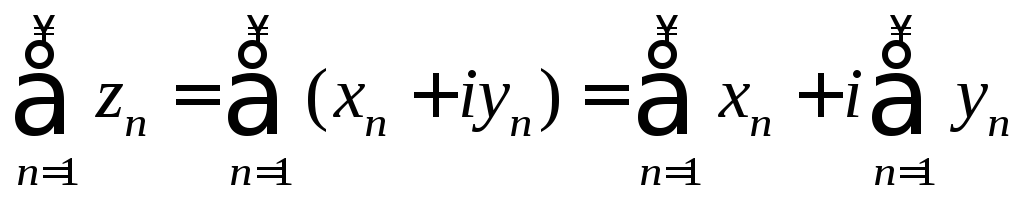● Ряд с комплексными членами сходится тогда и только тогда, когда сходятся ряды из действительных частейи мнимых частейчленов данного ряда. При этом, еслиА и В – соответственно сумма двух последних рядов, то сумма исходного ряда

Следствие. Если хотя бы один из рядов ,– расходящийся числовой ряд, то расходится исходный ряд с комплексными членами.

Пример. Исследовать на сходимость ряд .

Решение. Запишем данный ряд следующим образом:

Далее исследуем ряды вещественных и мнимых частей соответственно. Ряд, составленный из вещественных частей сходится, что следует из сравнения его членов с членами сходящегося ряда ДирихлеОднако числовой ряд, составленный из мнимых частей членов данного ряда,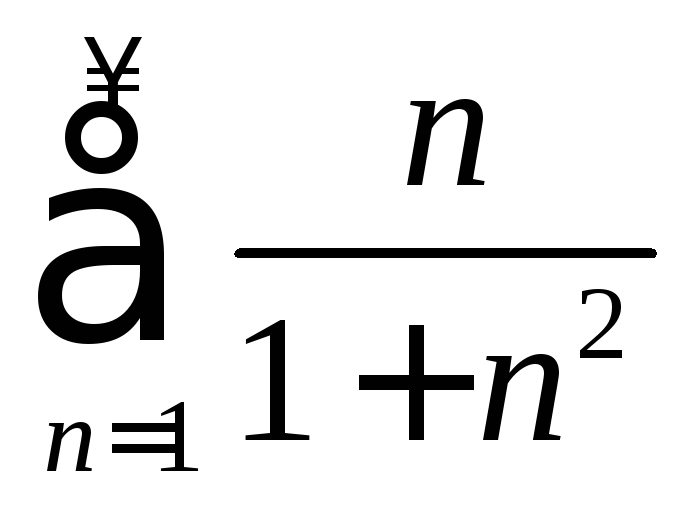расходится вместе с несобственным интегралом(интегральный признак Коши). Следовательно, данный ряд– расходящий.

● Ряд с комплексными членами сходится, если сходится ряд модулей его членовКак и в случае с действительными членами исходный ряд называетсяабсолютно сходящимся.

Пример. Исследовать на сходимость ряд

Решение. Составляем ряд модулей членов данного ряда:

К ряду модулей применим радикальный признак Коши:

Так как этот предел меньше единицы, то ряд модулей сходится. Следовательно, данный ряд сходится абсолютно.

12.4. Функциональные и степенные ряды

12.4.1. Область сходимости. Интервал сходимости

● Область сходимости функционального ряда – это множество тех значенийх, при которых функциональный ряд обращается в числовой сходящийся ряд.

● Область сходимости степенного ряда (согласно теореме Абеля) вырождается в интервал, который называется интервалом сходимости.

● Чтобы найти область (интервал), сходимости, нужно решить относительно х одно из неравенств:

или

Замечание. Необходимо дополнительно исследовать на сходимость на концах области (интервала) сходимости числовые ряды, которые получаются из функционального (степенного) ряда.

12.4.2. Равномерная и неравномерная сходимость

По определению предела числовой последовательности ряд

сходится в данной области, если, как бы мало ни было число , можно указать такое целое числоN, что при всех выполняется неравенство. В этом случае для функциональных рядов могут представляться два случая:

1. Можно найти число N, общее для всех значений х, входящих в область сходимости ряда, в этом случае записанный выше ряд называется равномерно сходящимся в данной области.

2. Такого общего числа N для всех х, лежащих в области сходимости, нет: каково бы ни было n, найдется в области сходимости такое число х, что . В этом случае в данной области рядсходится неравномерно.

Признак (Вейерштрасса) равномерной сходимости ряда

Ряд равномерно сходится в данной области, если существует такой сходящийся числовой ряд положительных членов, что для всех значенийх, лежащих в этой области, имеет место неравенство: . В этом случае числовой рядназываетсяможорантой функционального ряда .

Пример. Ряд – равномерно сходящийся в любой области,т. к. числовой ряд – абсолютно сходящийся и .

(Числовой ряд – сходящийся ряд Дирихле).