0735409_F4E1E_spravochnik_po_matematike / Эл. м. 6

.

Замечание. Криволинейный интеграл второго рода по замкнутому контуру обозначается символом: .

7.7.3. ФОРМУЛА ГРИНА

Пусть l – замкнутая кривая на односвязанной области G плоскости . Плоская область G называется односвязанной, если каков бы ни был замкнутый контур l, лежащий внутри этой области, ограниченная этим контуром конечная часть плоскости целиком принадлежит G.

Пусть l ограничивает конечную часть D. В области D заданы непрерывные функции и , имеющие в этой области непрерывные частные производные. Тогда справедлива формула Грина

,

где направление на контуре l выбрано так, чтобы при движении по контуру область D все время оставалась слева.

Если граница l области D состоит из нескольких отдельных контуров, то интеграл означает сумму интегралов, взятых по составляющим контурам, причем по каждому из них берется то направление обхода, при котором сама область D остается слева (рис. 43).

Рис. 43

7.7.4. УСЛОВИЯ НЕЗАВИСИМОСТИ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА ВТОРОГО РОДА

● Для односвязной области G следующие утверждения равносильны.

1. Интеграл , взятый по любому замкнутому контуру, лежащему в G, равен нулю.

2. Интеграл не зависит от пути интегрирования, а зависит только от начальной и конечной точек.

3. Выражение представляет собой полный дифференциал некоторой функции , однозначно определенной в области G.

4. Всюду в области G выполняется равенство .

● Условие независимости криволинейного интеграла второго рода от пути интегрирования состоит в следующем:

Криволинейный интеграл не зависит от пути интегрирования в том и только в том случае, когда подинтегральное выражение есть полный дифференциал некоторой функции , т. е. если .

Замечание. Поскольку выше сформулированные условия 1–4 равносильны, то любое из них можно считать условием независимости криволинейного интеграла от пути интегрирования.

8. ПРИЛОЖЕНИЯ КРАТНЫХ И КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ

8.1. Геометрические приложения

8.1.1. ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПЛОСКОЙ ФИГУРЫ

D₂

ρ = ρ₂(φ)

0 ρ = ρ₁(φ)

φ₁

φ₂

ρ

D₂

;

Пример 3.2. Вычислить площадь фигуры, являющейся пересечением кардиоиды и окружности (рис. 44).

Решение. Так как фигура имеет ось симметрии, то ее можно представить в виде суммы областей:

т. к.

Область может быть описана системой неравенств

Таким образом, площадь заштрихованной фигуры S вычисляется следующим образом:

(кв. ед.).

8.1.2. ВЫЧИСЛЕНИЕ ДЛИНЫ ДУГИ

где dl определяются в зависимости от способа задания кривой АВ:

1) если кривая АВ задана явно:

2) если уравнение кривой АВ задано в полярной системе координат: .

3) если кривая АВ задана параметрически

4) если кривая АВ задана параметрически в пространстве:

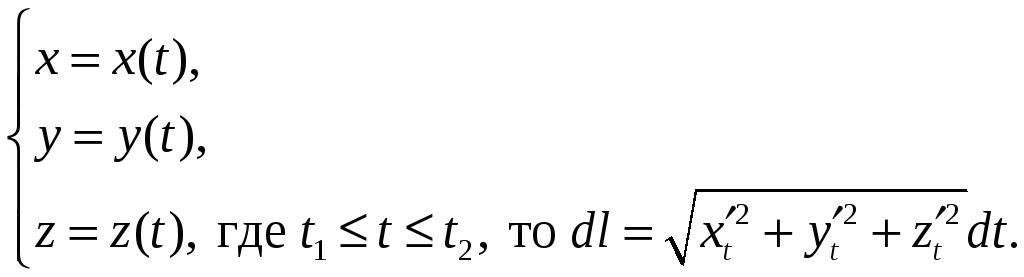
8.1.3. ОБЪЕМ ТЕЛА

● Объем цилиндрического тела с основанием D в плоскости и ограниченного сверху поверхностью можно рассчитать с помощью двойного интеграла .

● Объем любой ограниченной замкнутой пространственной области V рассчитывается с помощью тройного интеграла: .

Пример. Вычислить объем шара радиуса R.

Решение. Вычисление объема проведем в сферических координатах по формуле где

8.2. Вычисление работы переменной силы

Пусть , и непрерывные функции на кривой . Если – переменная сила, то работа, совершаемая этой силой F вдоль пути определяется формулой

Следствие. Работа переменной силы вдоль плоской кривой определяется аналогично по формуле: .

113