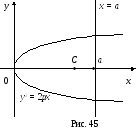
Пример 5.3. Определить координаты центра тяжести однородной фигуры

, ограниченной кривой и прямой.

Решение. В силу симметрии фигуры относительно оси (рис. 45) центр тяжести лежит на оси, а потому. Абсциссу центра тяжести определим по формуле

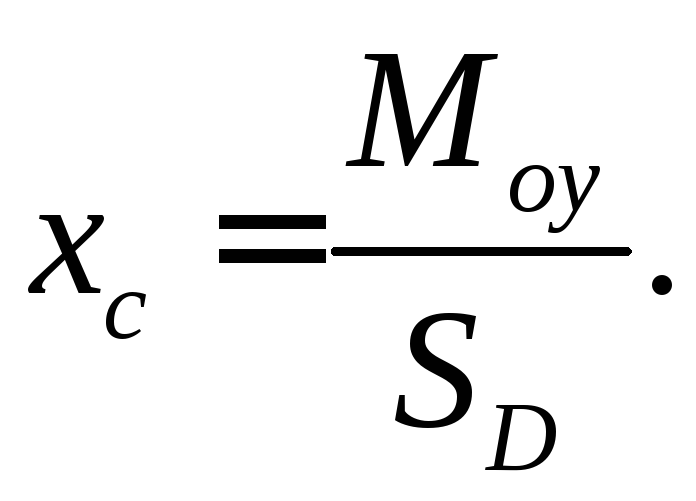
Вычислим отдельно:

числитель дроби

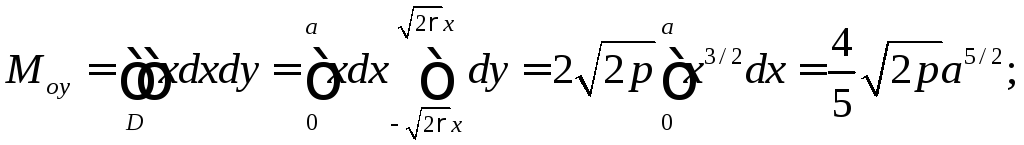
знаменатель дроби

Следовательно, абсцисса центра тяжести однородной фигуры

Итак, центр тяжести расположен в точке

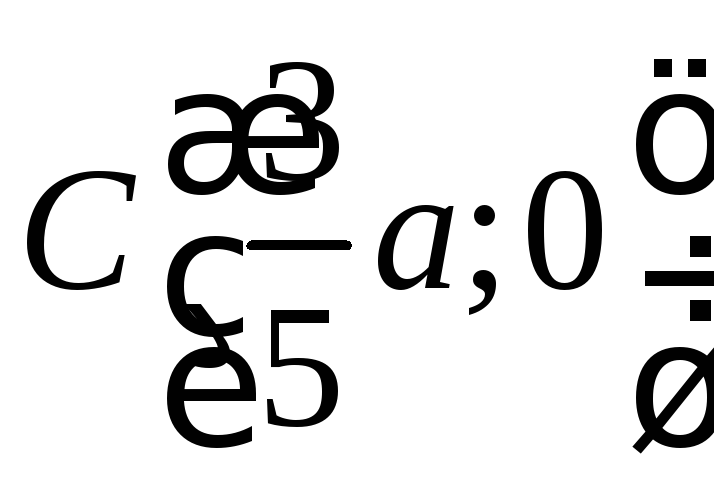
9. Понятие интегралов на поверхности

9.1. Поверхностный интеграл первого рода

Пусть непрерывная функция задана на гладкой поверхности σ. (Гладкой называется поверхность, имеющая в каждой своей точке касательную плоскость, положение которой меняется непрерывно при переходе от точки к точке.) Для вычисления поверхностного интеграла первого родапо поверхности σ, заданной уравнениемгде– дифференцируемая функция, предположим, что поверхность σ однозначно проектируется на плоскостьв областьD. Поскольку , то получим:

.

Итак, вычисление поверхностного интеграла первого рода свелось к вычислению соответствующего двойного интеграла по области D – проекции поверхности σ на плоскость .

9.2. Понятие о двусторонней поверхности

Пусть σ – некоторая гладкая поверхность. Зафиксируем на ней точку и одно из двух направлений нормали к ней в этой точке, указав единичный векторn, отложенный из . Проведем через точкузамкнутую линию Г, целиком лежащую на поверхности σ и не имеющую общих точек с границей σ. Будем совершать обход линии Г так, чтобы нормаль изменялась непрерывно, при этом векторn в каждой точке М будет иметь вполне определенное направление (вообще говоря, отличное от направления в точке ). По возвращении в точкупосле совершения обхода может оказаться: 1) векторn принял первоначальное направление; 2) вектор n изменил направление на противоположное.

Поверхность σ называется двусторонней, если обход по любой замкнутой линии, лежащей на этой поверхности и не имеющей общих точек с ее границей, не меняет направления нормали к поверхности.

Двусторонней поверхностью является всякая гладкая поверхность, определяемая уравнением. Действительно, выбрав направление нормального вектораn₁ к ней так, чтобы он составил с осью острый угол, получим одну сторону поверхности (верхнюю). Выбрав это направление так, чтобы нормальный векторn₂ составил с осью тупой угол, получим

другую сторону поверхности (нижнюю). В частности, плоскость и всякая ее часть (круг и т. п.) – двусторонняя поверхность. Любая замкнутая поверхность, не имеющая точек самопересечения (сфера, эллипсоид и др.), также является двусторонней. В самом деле, направив нормальный вектор внутрь объема, ограниченного этой поверхностью, получим одну сторону поверхности (внутреннюю), направив нормаль вне указанного объема, – другую сторону поверхности (внешнюю).

Двустороннюю поверхность называют также ориентируемой, а выбор ее определенной стороны – ориентацией поверхности.

Если на поверхности существует замкнутая линия, обход по которой меняет направление нормали, то поверхность называется односторонней. Простейшим примером односторонней поверхности является лист Мёбиуса.

9.3. Поверхностный интеграл второго рода

Рассмотрим функцию , определенную и непрерывную на гладкой ориентируемой поверхности σ, которая задана уравнениеми которая проектируется на плоскостьв область. Для верхней стороны поверхности σ, т. е. в случае, когдагде γ – угол между нормалью к поверхности и осьюполучим:

.

Для нижней стороны поверхности, т. е. в случае, когда получим:

.

Итак, поверхностный интеграл второго рода вычисляется с помощью двойного интеграла по плоской области D – проекции поверхности σ на плоскость .

Замечания.

1. Аналогично вычисляются поверхностные интегралы второго рода по координатам и:

2. Формулы приложения интегралов по поверхности аналогичны соответствующим формулам геометрических и механических приложений в двойном и тройном интеграле.