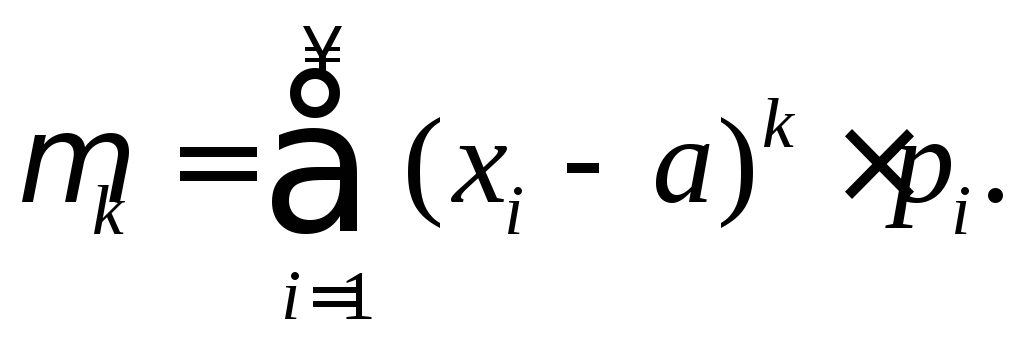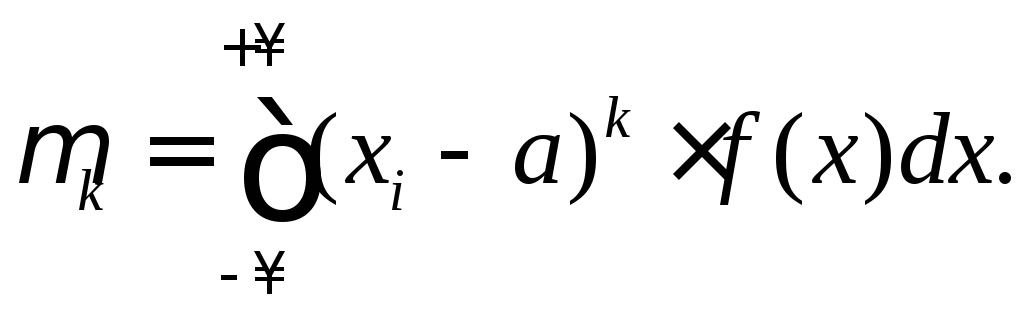14. Теория вероятностей. Справочные материалы для решения задач
|
№№ п/п |
Понятия, обозначения |
Содержание, формула |
|
1 |
2 |
3 |
|
1 |
Множество |
Множество
|
|
2 |
Дополнение
|
|
|
3 |
Равенство
множеств |
Два
множества
|
|
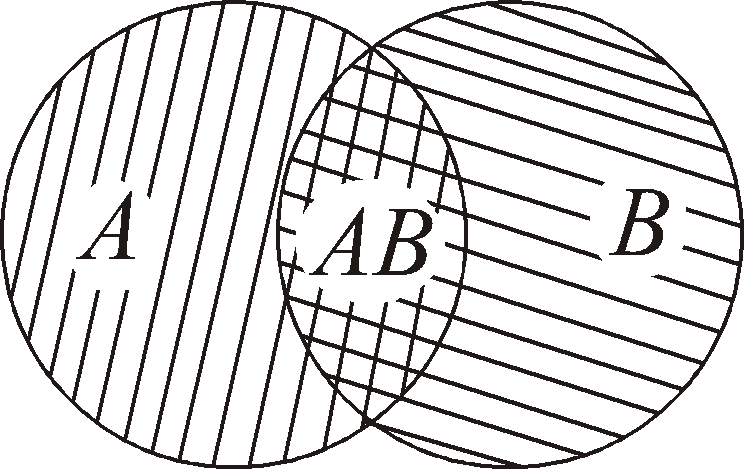
4 |
Объединение
(сумма) множеств
|
Множество
|
|
5 |
Пересечение
(произведение)
множеств
|
Множество
|
|
6 |
Разность
двух
множеств
|
|
|
7 |
Эквивалентные множества |
Два множества называются эквивалентными, если между ними установлено взаимно-однозначное соответствие. |
|
8 |
Счетные множества |
Бесконечные
множества, эквивалентные множеству
натуральных чисел
|
|
9 |
Перестановки. Число перестановок |
Соединения,
отличающиеся только порядком
элементов, называются перестановками.
Число перестановок из
|
|
10 |
Размещения. Число размещений |
Соединения
из
|
|
1 |
2 |
3 |
|
11 |
Сочетания. Число сочетаний |
Соединения
из
|
|
12 |
Стохастический эксперимент |
Это опыт (испытание), результат которого заранее не определен |
|
13 |
Достоверное событие |
Результат, который обязательно наступает при осуществлении данного комплекса условий (опыта, эксперимента) называется достоверным событием |
|
14 |
Случайное событие |
Это событие, которое может произойти, а может и не произойти в данном испытании |
|
15 |
Невозможное событие |
Это событие, которое не может произойти при данном комплексе условий |
|
16 |
Относительная
частота события
|
Отношение
|
|
17 |
Статистическое определение вероятности |
Если
при неограниченном увеличении числа
экспериментов относительная частота
события
|
|
18 |
Определение вероятности в классической схеме |
|
|
1 |
2 |
3 |
|
19 |
Вероятность
суммы
(объединения),
двух
событий
|
|
|
20 |
Вероятность
произведения двух зависимых
событий
|
где |
|
21 |
Независимые
события
|
Это
такие события, для которых
Следовательно, |
|
22 |
Схема Бернулли |
Стохастический
эксперимент состоит из последовательности
|
|
23 |
Формула Бернулли |
Вероятность
того, что в серии из
|
|
Вероятность
того, что при
| ||
|
24 |
Формула Пуассона |
При
достаточно большом
|
|
| ||
|
25 |
Локальная формула Муавра-Лапласа |
При
достаточно большом
|
|
1 |
2 |
3 |
|
26 |
Интегральная формула Муавра – Лапласа |
где
|
|
27 |
Понятие случайной величины |
Случайной величиной называют переменную величину, которая принимает числовые значения в зависимости от исходов испытания случайным образом. |
|
28 |
Понятие
дискретной
случайной
величины
(ДСВ
|
ДСВ
|
|
29 |
Закон распределения дискретной случайной величины |
Соответствие
между значениями
Если
ДСВ
|
|
1 |
2 |
3 |
|
30 |
Понятие
непрерывной
случайной
величины
(НСВ
|
НСВ
|
|
31 |
Функция распределения. Свойства функции распределения |
Функцией
распределения случайной величины
Функция
распределения
Функция является разрывной.
Случайная
величина
Вероятность
того, что СВХ примет значение из
промежутка
Свойства функции распределения 1. 2.
Если
|
|
1 |
2 |
3 |
|
31 |
Функция распределения. Свойства функции распределения |
3.
Функция
4.
Если все возможные значения СВХ
принад-лежат
интервалу
5.
Если все возможные значения СВХ
принад-лежат
бесконечному интервалу
Если
Отсюда следует, что для непрерывной случайной величины выполняются равенства:
|
|
32 |
Плотность распределения вероятностей непрерывной случайной величины. Свойства функции плотности распределения. |
Плотностью
распределения (дифференциальной
функцией распределения) вероятностей
НСВ
Следовательно,
Вероятность
того, что НСВХ примет значение,
принадлежащее интервалу
|
|
1 |
2 |
3 |
|
32 |
Плотность распределения вероятностей непрерывной случайной величины. Свойства функции плотности распределения. |
Зная
плотность распределения, можно найти
функцию распределения
Свойства функции плотности 1.
Плотность распределения 2.
Несобственный интеграл по бесконечному
промежутку
3.
Если все возможные значения случайной
величины принадлежат отрезку
|
|
33 |
Математическое ожидание |
Для
ДСВ
Для
НСВ
где
|
|
34 |
Свойства математического ожидания |
1) 2)
3) 4)
Если
|
|
1 |
2 |
3 |
|
35 |
Дисперсия случайной величины |
Разность
Математическое
ожидание отклонения равно нулю:
Дисперсией,
или рассеянием случайной величины
|
|
36 |
Свойства дисперсии |
1)
2)
3)
Если случайные величины
4)
5)
|
|
37 |
Среднее квадратическое отклонение |
Среднеквадратическим
отклонением, или стандартным
отклонением, случайной величины
|
|
38 |
Биномиальное распределение |
Закон распределения дискретной случайной величины, определяемой формулой Бернулли
называется
биномиальным. Постоянные
|
|
39 |
Распределение Пуассона |
Распределением
Пуассона называется распределение
вероятностей дискретной случайной
величины, определяемое формулой
Пуассона
|
|
1 |
2 |
3 |
|
40 |
Равномерное
распределение на интервале
|
Если
значения случайной величины, которые
она принимает в конечном промежутке
Доказано,
что
|
|
41 |
Геометрическое распределение |
Геометрическим
называется распределение дискретной
случайной величины
|
|
42 |
Показательное распределение |
Показательным
называется распределение с плотностью
вероятностей, определяемой по формуле
где
Замечание.
Если
|
|
1 |
2 |
3 |
|
43 |
Нормальное
распределение
|
Нормальным распределением, или распределением Гаусса, называется распределение с плотностью вероятностей
Постоянные
Вероятность
попадания значений нормальной
случайной величины
где
|
|
44 |
Нормированное
распределение
|
Нормированным
или стандартным называется такое
нормальное распределение непрерывной
случайной величины, когда функция
плотности вероятностей
|
|
45 |
Мода
случайной величины
|
Модой
ДСВ
Модой
НСВ
|
|
46 |
Медиана
|
Медианой
непрерывной случайной величины
Если
прямая
|
|
1 |
2 |
3 |
|
47 |
Начальные
моменты
|
Начальным
моментом
Для
ДСВ
Начальный
момент
|
|
48 |
Центральные
моменты
|
Центральным
моментом
Для
ДСВ
если
множество этой величины конечно, а
если – счетно, то
Для
НСВ
|
|
49 |
Некоторые свойства начальных и центральных моментов |
|
|
1 |
2 |
3 |
|
50 |
Асимметрия |
Отношение
центрального момента 3-го порядка к
кубу среднеквадратического отклонения
случайной величины называется
асимметрией:
Если распределение случайной величины симметрично относительно ее математического ожидания, то асимметрия равна нулю. |
|
51 |
Эксцесс |
Эксцессом
случайной величины называется
величина
Для
нормального распределения
Кривые,
более островершинные по сравнению
с нормальной кривой Гаусса, имеют |

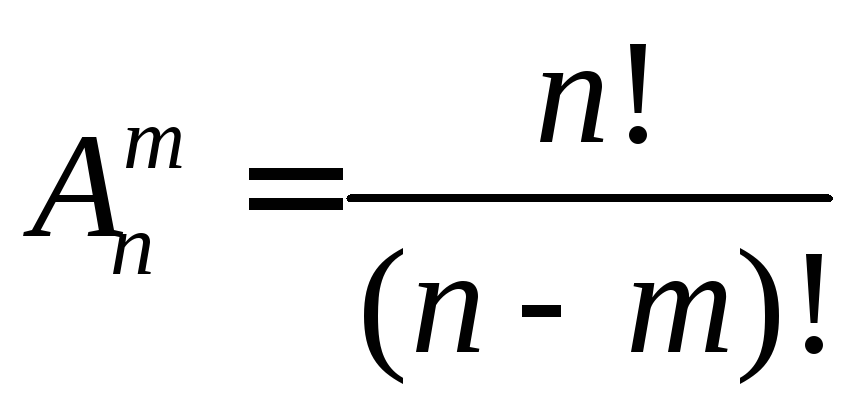

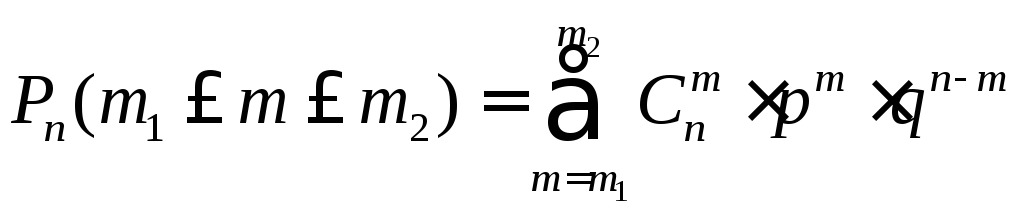
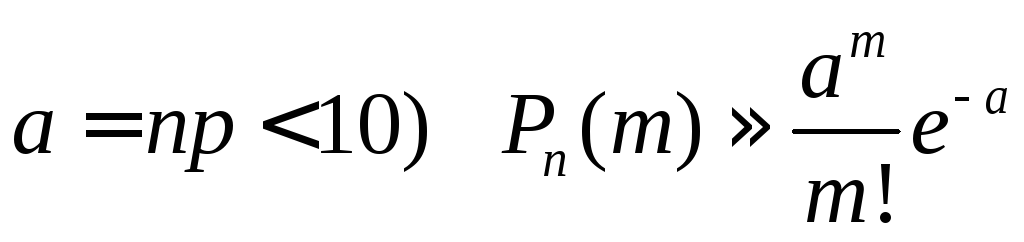 (таблица 1)
(таблица 1)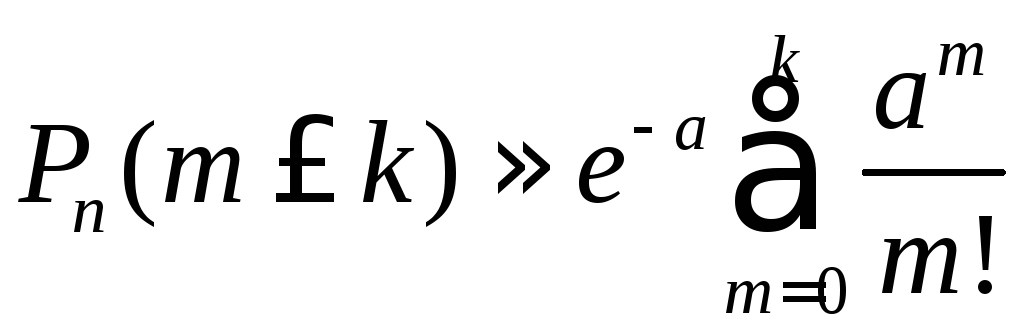 (таблица
2)
(таблица
2)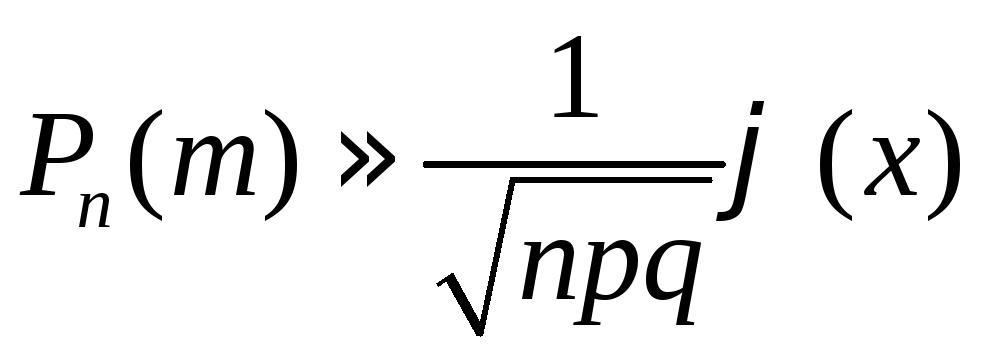 ,
где
,
где
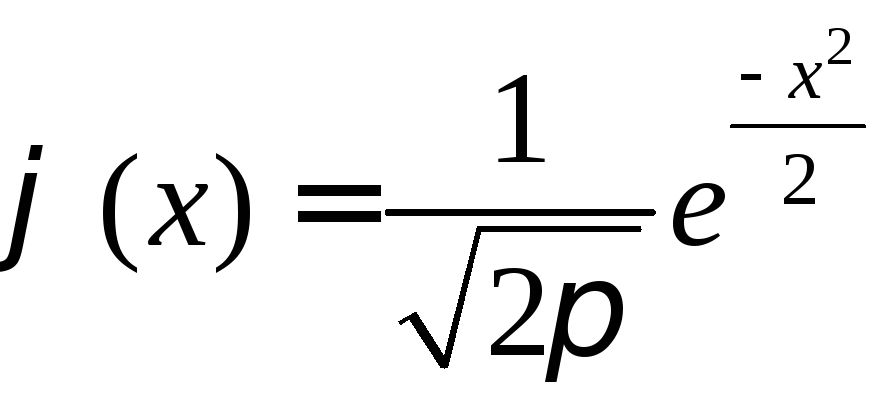 и
и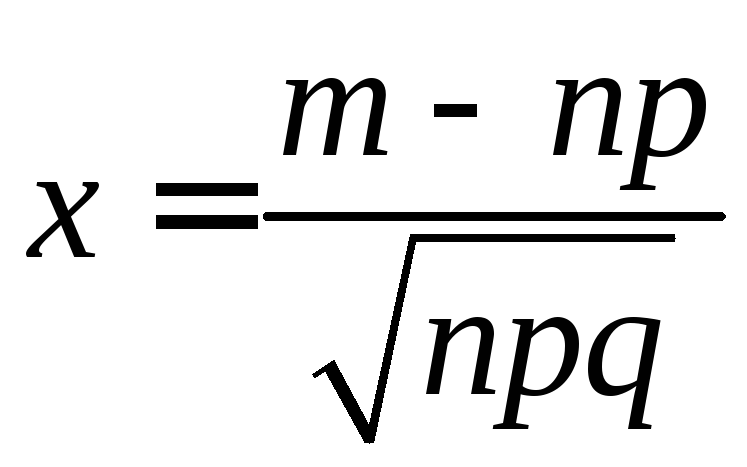 ;
;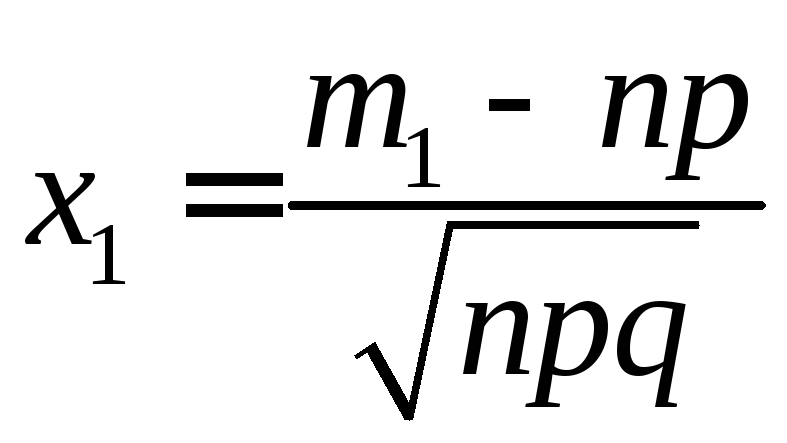 ;
; ;
;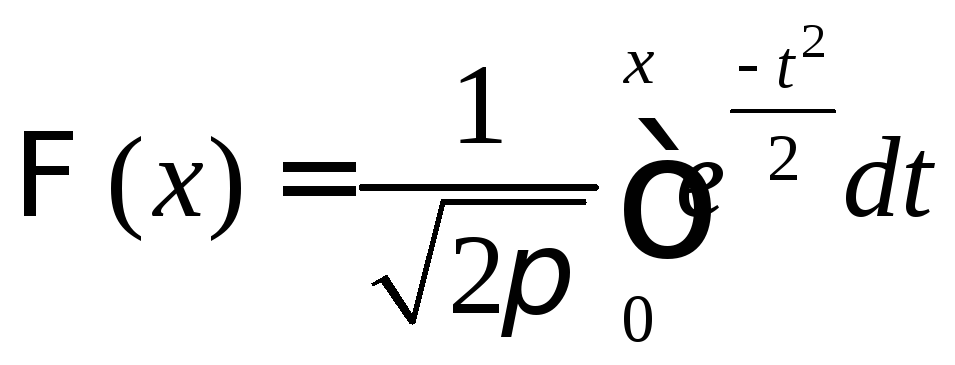 ;
;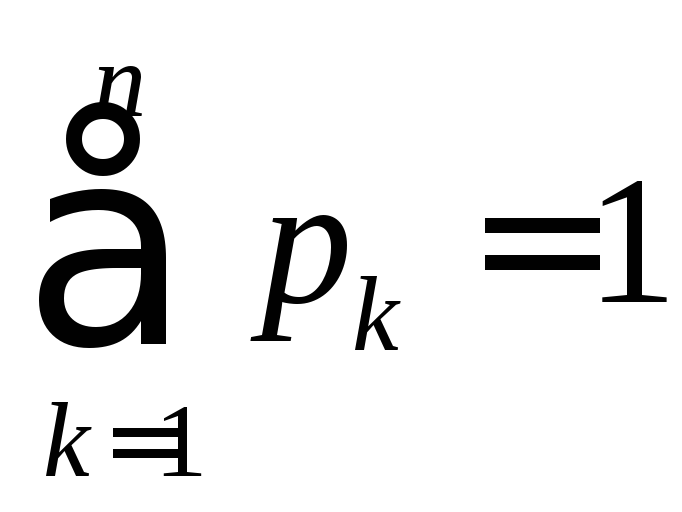
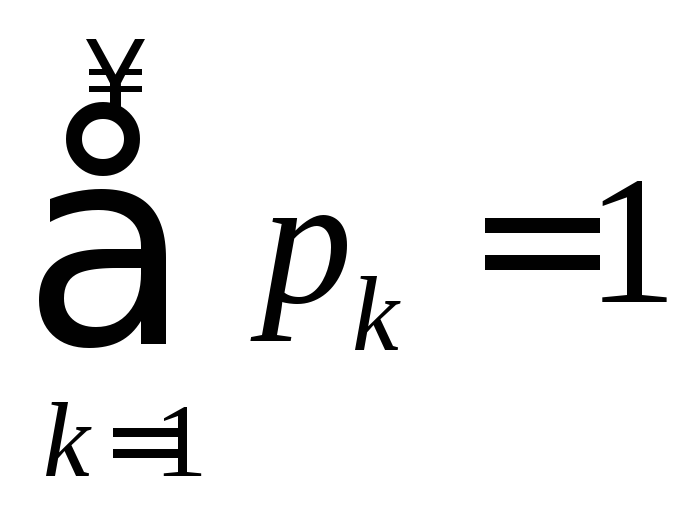
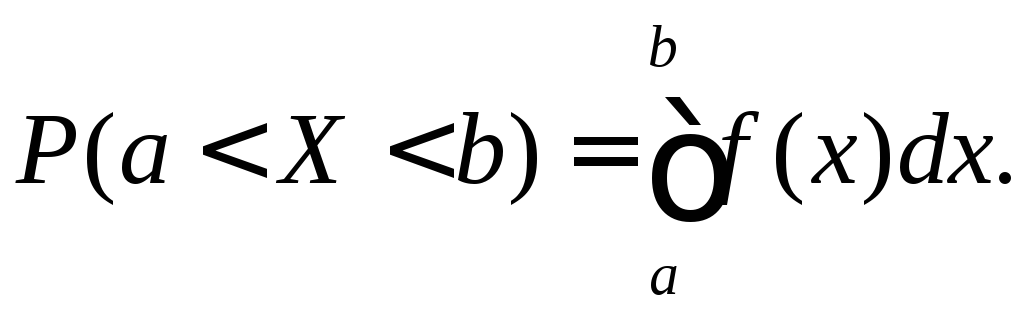
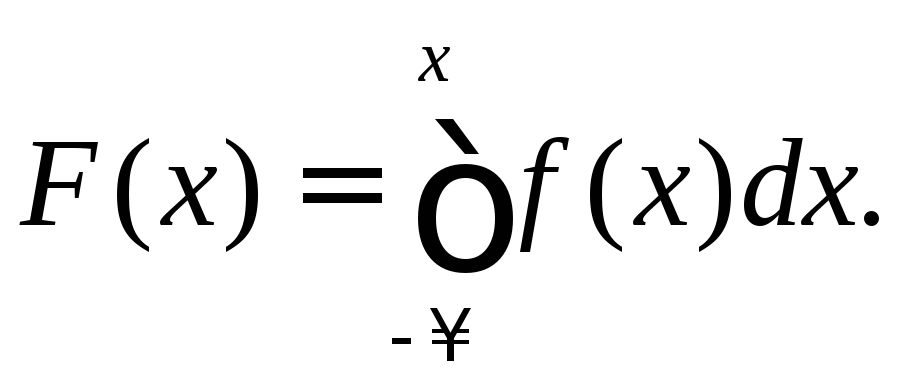
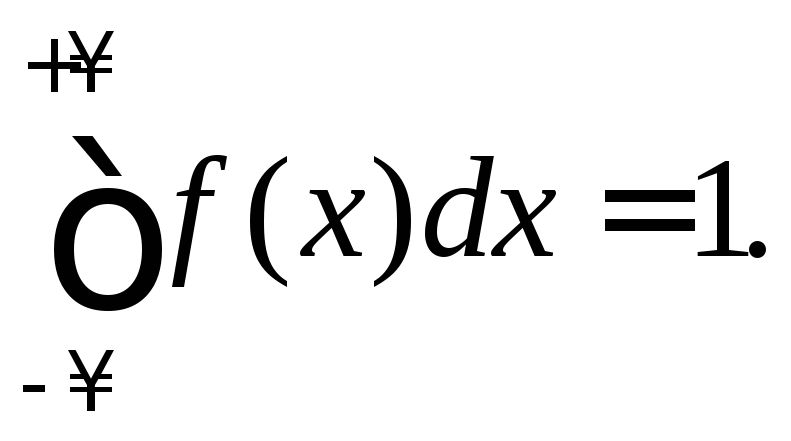
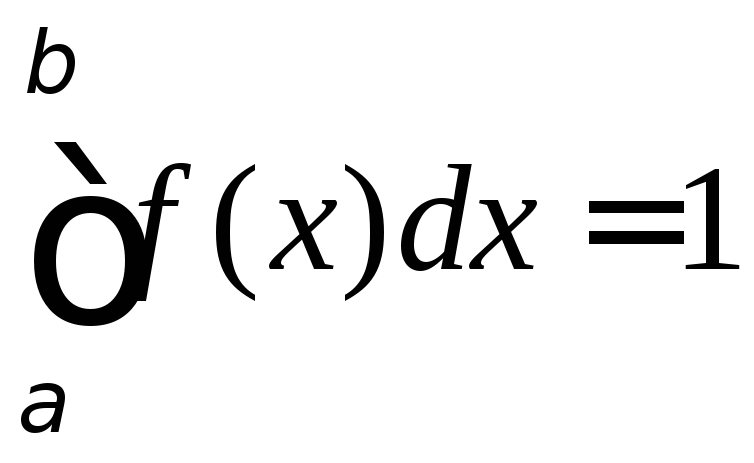 ,
так как вне этого промежутка
,
так как вне этого промежутка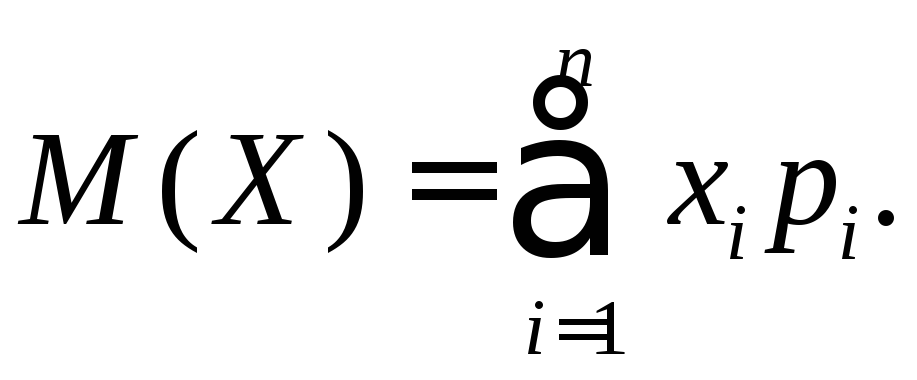
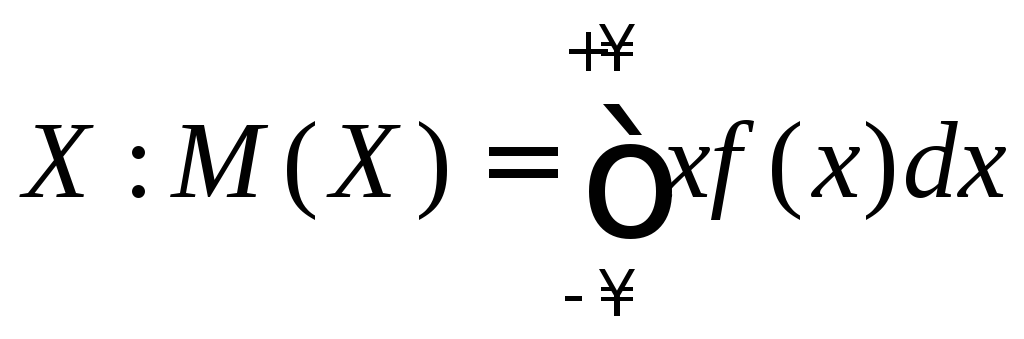 ,
,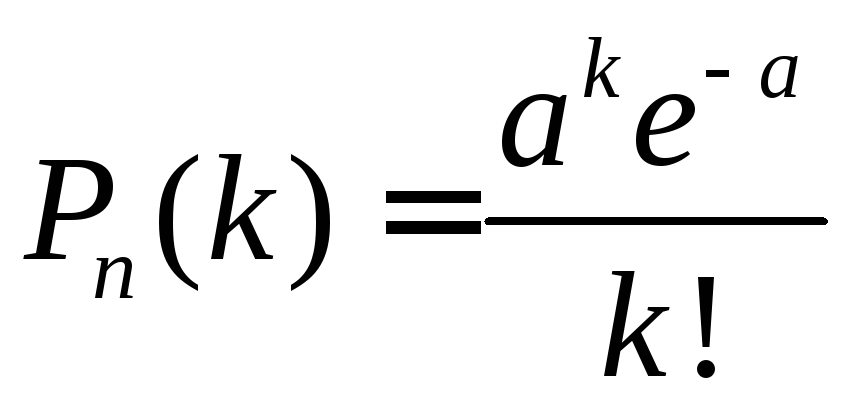 ,
где
,
где
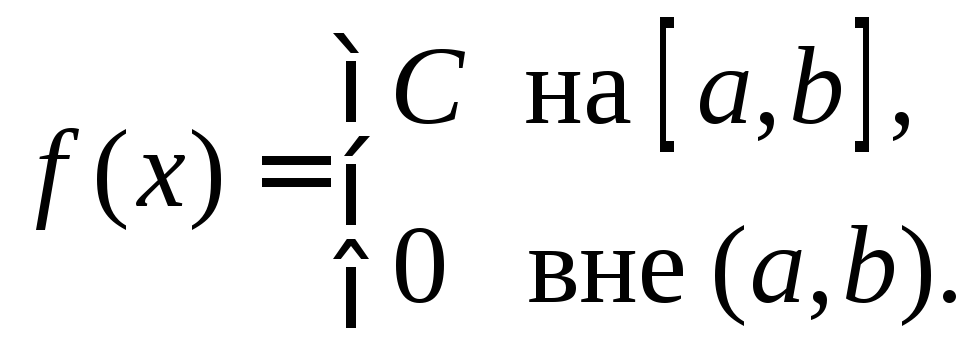
 ;
;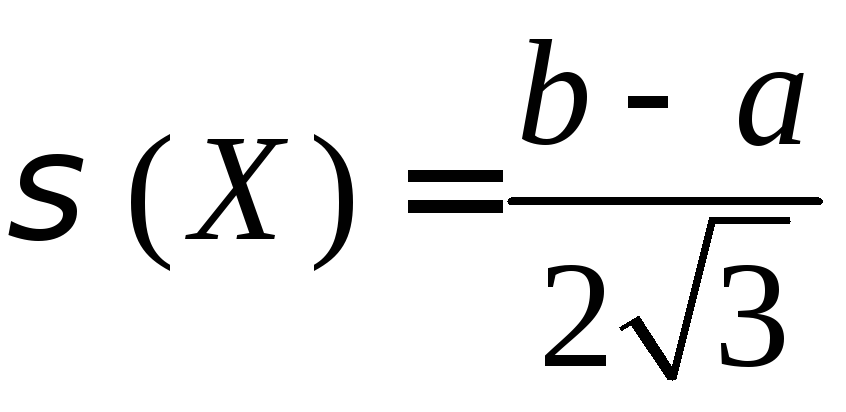
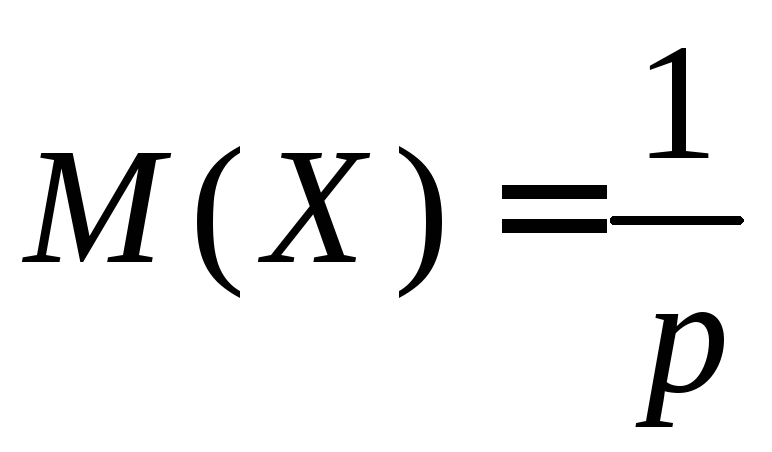 ;
;



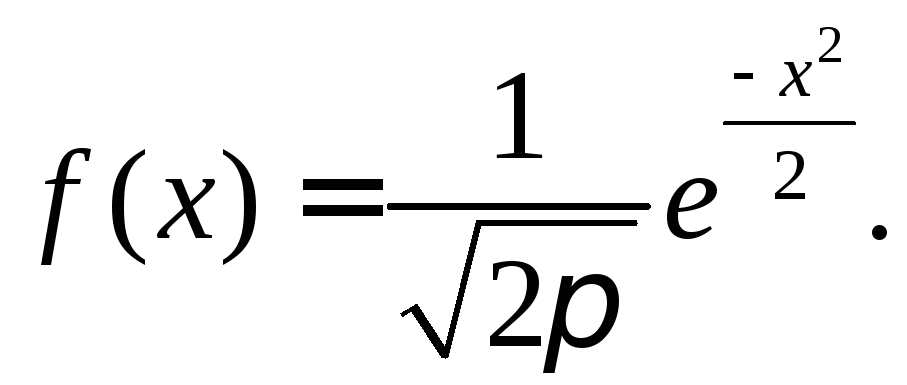
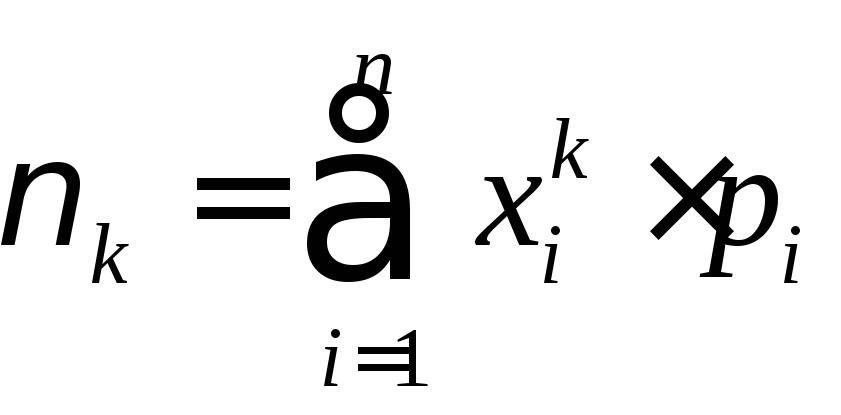 ,
где
,
где
 .
.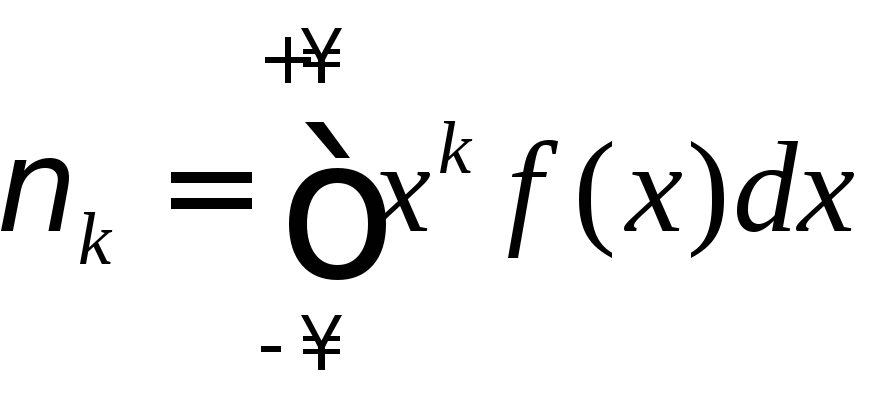 ,
где
,
где
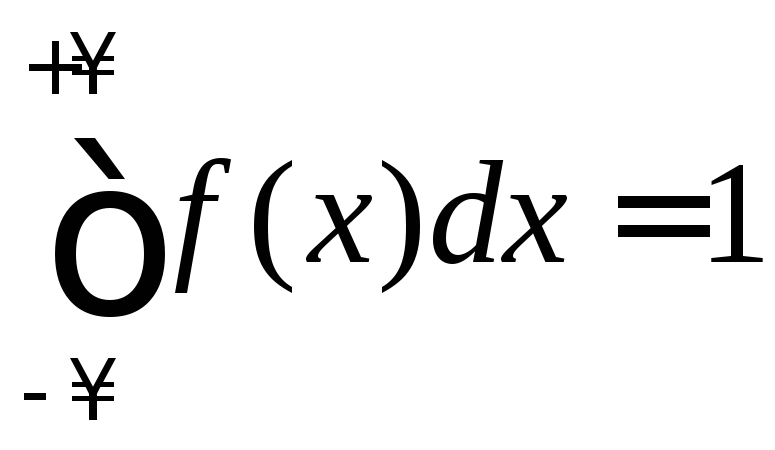 .
.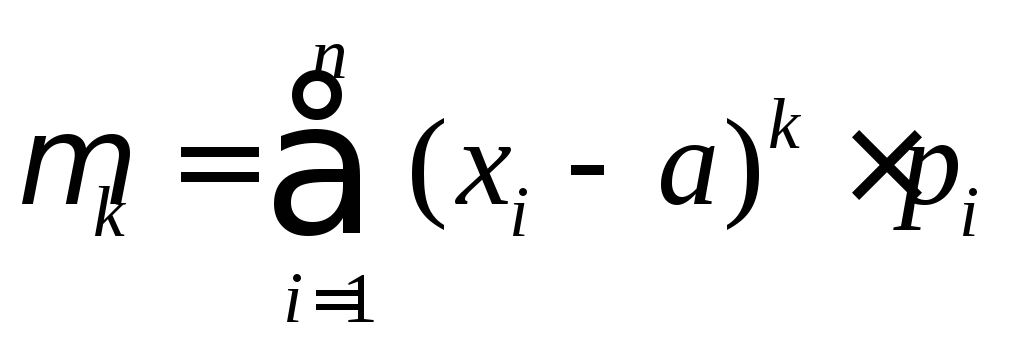 ,
,