28. Теорема о существовании точки равновесия в случае смешанных стратегий. Теорема о цене игры в случае применения одним из игроков чистых стратегий.

Какова бы не была матрица А в антагонистической игре, ситуация равновесия всегда существует, то есть выполняется определение равновесия и выполняется условие:

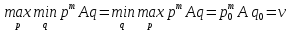
Цена игры может быть достигнута даже в том случае, когда один игрок применяет чистые стратегии, а другой – смешанные, причем экстремум достигается на оптимальной смешанной стратегии.

Обозначим 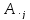– столбец j. 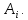– строка i.

Если первый игрок применяет чистые стратегии (строчки), то 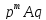переходит в выражение: .

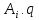Если второй игрок применяет чистые стратегии (столбцы), то 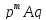переходит в выражение .

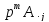Т.е. имеет место равенство:

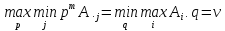
Внешний экстремум на смешанных стратегиях, внутренний – на чистых.

29. Связь цены игры с нижней ценой игры и верхней ценой игры.

Цена игры находится между максимином и минимаксом

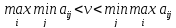
То есть, цена игры находится между нижней ценой игры и верхней ценой игры.

30. Графическое решение игры в случае наличия у одного из игроков двух чистых стратегий.

Если у одного из игроков имеется только две стратегии, то игру можно решить графическим методом (найти смешанные оптимальные стратегии и цену игры).

У кого две стратегии – тот экстремум внешний.

1. Определяем максимин и минимакс. Цена игры лежит между этими числами.

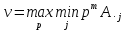2. – перебираем все чистые стратегии второго по очереди, выбираем минимум из них.

Две стратегии игрока раскладываем в виде 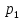, 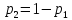(т.к. вероятность равна единице – игрок все равно выберет какую-то из своих двух стратегий).

3. Определяем выигрыши первого игрока, когда он применяет свою смешенную, а второй свои чистые стратегии.

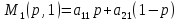
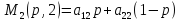
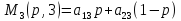
Строим эти прямые (одна точка при p=0, вторая – при p=1).

Если мы перебираем чистые стратегии второго игрока (столбцы), то на графике нужно строить нижнюю огибающую (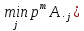 и искать на ней верхнюю точку (.

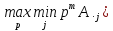Если же две стратегии у второго игрока, то 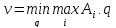– т.е. перебираем все чистые стратегии первого игрока по очереди, выбираем максимум из них.

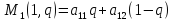
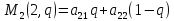
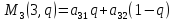
Аналогично строим прямые (одна точка при q=0, другая – при q=1). В этом случае нужна верхняя огибающая (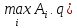 и нижняя точка на ней (.

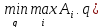31. Доминирующие и доминируемые стратегии. Упрощение матрицы игры. Вероятности доминируемой стратегии в оптимальной смешанной.

Доминирующая стратегия – стратегия, которая приносит игроку больший выигрыш, чем другие.

Доминируемая стратегия – стратегия, которая не приносит лучшего результата, по сравнению с остальными.

Для того, чтобы 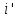являлась доминирующей стратегией первого игрока по отношению к стратегии i, если имеет место равенство: 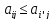для всех j.

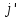является доминирующей стратегией второго игрока по отношению к j, если

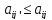
Вероятности доминируемых стратегий в оптимальной смешанной равны 0.

Поэтому можно упростить матрицу, вычеркнув «невыгодные» строки и столбцы.

Вычеркиваются «слишком тонкие» строки (каждый элемент такой строки меньше или равен элементу другой строки). Т.е. используя стратегию, соответствующую «слишком тонкой» строке, игрок выиграет меньше, чем мог бы.

Вычеркиваются «слишком толстые столбцы» (каждый элемент столбца больше или равен элементу другого столбца). Т.е., следуя данной стратегии, второй игрок проиграет больше, чем мог бы.

Упрощая платежную матрицу, мы приходим в состояние, когда у одного из игроков остается только две стратегии. Тогда возможно решить игру графическим способом.