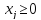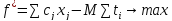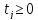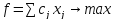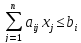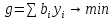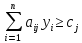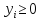9. Теорема об оптимальном решении кзлп и вершине области

Если задача линейного программирования имеет оптимальное решение, то оно достигается хотя бы в одной из вершин.

Доказательство:

Допустим, что задана целевая функция на максимум: 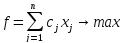. Тогда её градиент имеет вид

Поскольку область допустимых решений является выпуклым многогранником (билет 6), то перемещая линию уровня параллельно самой себе по направлению вектора градиента, придем в вершину или точку на границе.

Доказательство только для случая с точкой на границе (отрезок области допустимых значений параллелен линии уровня (альтернативное решение)).

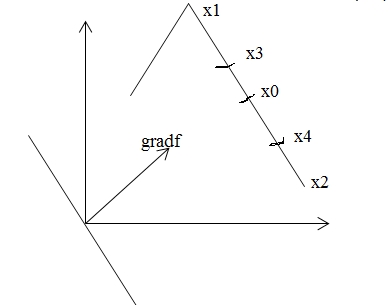
Предположим, что достигнуто во внутренней точке какого-то отрезка, а – координаты вершин (концов) отрезка.

Необходимо показать, что значение целевой функции в этих трех точках будет совпадать.

Возьмем произвольные точки на отрезке (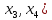. Тогда может быть выражена через эти точки: (говоря научным языком, мы представляем внутреннюю точку как выпуклую комбинацию вершин).

Подставим это выражение в целевую функцию: . В силу линейности функции мы можем вынести константы (λ, 1-λ) за знак функции.

.

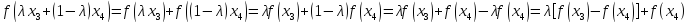Так как 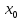– оптимальная точка (т.е. в ней достигается максимум целевой функции), то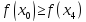, из этого следует, что , следовательно,

Точку 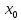, с другой стороны, можно переписать как .

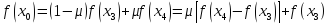Опять же, целевая функция на максимум, – оптимальная точка, соответственно в ней этот максимум и достигается. Следовательно, значение функции в этой точке должно быть больше или равно значению функции в соседней точке 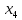(. Поэтому 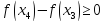, следовательно,

Теперь остается сравнить два выражения: 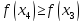и 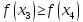. Понятно, что значение функции не может быть одновременно и больше и меньше определенного числа, следовательно, 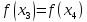. Если подставить это в любое выражение выше получим, что и 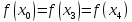. Так как точки 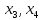были взяты на отрезке 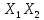, то и значение функции на концах отрезка равно 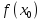, т.е. .

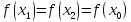Из этой и предыдущей теоремы следует, что оптимальное решение нужно искать среди базисных.

10. Симплексный метод. Приведение злп к канонической форме. Балансовые переменные. Выбор разрешающего элемента.

(а) Признак оптимального базисного решения

(b) Признак неоптимального базисного решения

(c) Признак неограниченного значения целевой функции

(d) Признак альтернативного решения

(e) Признак вырожденного решения.

Для решения ЗЛП симплекс-методом необходимо привести задачу к канонической форме (см. билет 1).

Предположим, что задача дана в стандартной форме:

;

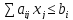(все х – неотрицательны, принимают значения от 1 до n)

Для приведения к канонической форме (ограничения в виде равенств), требуется ввести балансовые переменные.

(балансовые переменные также неотрицательны).

В целевую функцию они записываются с нулевым коэффициентом.

На первом этапе балансовые переменные являются базисными. Из столбцов коэффициентов при балансовых переменных можно составить единичную матрицу.

Задача решается в виде таблицы:

Строка целевой функции (f(x)) называется индексной строкой. Коэффициенты в индексной строке – оценки. Записываются как коэффициенты перед соответствующими х со знаком минус.

Если в строке целевой функции нет отрицательных оценок, то найдено оптимальное решение. При этом значения базисных переменных совпадают со значением столбца свободных членов, а свободные переменные равны 0.

Столбец свободных членов - – правые части ограничений.

Если среди оценок есть отрицательные, то требуется получить улучшенное решение, т.е. построить новую таблицу по правилу:

1. Нужно выбрать разрешающий столбец. Им может быть любой столбец с отрицательной оценкой в строке целевой функции, но обычно выбирают самую большую по модулю отрицательную оценку (т.е. самую отрицательную из всех).

Та переменная, которая соответствует выбранному разрешающему столбцу, станет базисной на следующем этапе.

2. Далее следует выбрать разрешающую строку. Для этого необходимо элементы столбца свободных членов разделить на элемент разрешающего столбца соответствующей строки. После этого выбрать минимальное соотношение.

Та переменная, которая соответствует выбранной разрешающей строке, выйдет из базиса на следующем этапе.

3. Элемент, который находится на пересечении разрешающего столбца и разрешающей строки, станет разрешающим элементом.

На следующем этапе он должен стать равным нулю, а все остальные элементы разрешающего столбца, включая оценку в индексной строке, должны равняться 0.

При переходе к следующей таблице первой заполняется разрешающая строка (сначала делаем единицу из разрешающего элемента, потом зануляем оставшиеся элементы разрешающего столбца, т.е. заполняем другие строки).

После пересчета таблицы смотрим, есть ли отрицательные оценки, если есть – повторяем шаги 1-3.

Если в индексной строке больше нет отрицательных оценок, то получено оптимальное решение.

Замечания:

1. Если при выборе разрешающего столбца есть несколько одинаковых наибольших по модулю отрицательных оценок, то можно выбрать любой столбец.

2. Если при выборе разрешающей строки несколько минимальных соотношений, то можно взять любую строку, даже если это отношение равно 0.

3. Если разрешающую строку можно выбрать неединственным способом, то на следующем этапе одна из базисных переменных будет равна 0, т.е. решение будет вырожденным.

Как увидеть различные варианты, возникающие при решении?

1. Неоптимальное базисное решение:

Есть отрицательные оценки, можно выбрать разрешающую строку.

2. Единственное оптимальное решение:

Базисные переменные	положительны, либо равны нулю
Оценки базисных переменных	равны нулю
Свободные переменные	равны нулю
Оценки свободных переменных	положительны

3. Вырожденное решение:

Базисные переменные	какая-то базисная переменная равна нулю
Оценки базисных переменных	равны нулю
Свободные переменные	равны нулю
Оценки свободных переменных	положительны

Вырожденное решение может быть и единственным.

4. Альтернативное решение:

Базисные переменные	положительны, либо равны нулю
Оценки базисных переменных	равны нулю
Свободные переменные	равны нулю
Оценки свободных переменных	какая-то оценка свободной переменной равна нулю

Чтобы найти альтернативное решение нужно свободную переменную, которая равна 0, сделать базисной, выбрав ее столбец в качестве разрешающего, и пересчитать таблицу как обычно.

Если решение вырожденное и оценка свободной переменной равна нулю, то могут быть дополнительные исследования

5. Область допустимых решений не пуста, целевая функция неограниченно возрастает.

Если имеется столбец с отрицательной оценкой (т.е. он может быть выбран разрешающим), но все элементы этого столбца отрицательны либо равны нулю, то целевая функция неограниченно возрастает.

Но не всегда при открытой области функция растет неограниченно. Это зависит от направления градиента: если он указывает направление 4 четверти, например, то оптимальное значение можно найти (в этом случае линии уровня идут «сверху вниз», т.е. оптимальной будет самая нижняя точка).

11. М-задача, искусственные переменные.

(а) Признак существования решения исходной задачи

(b) Признак несовместимости области допустимых решений ЗЛП

Если дано ограничение в сторону больше или равно и нужно перейти к канонической форме (т.е. получить ограничения в виде равенств), то вводится балансовая переменная со знаком минус и кроме того, вводится переменная искусственного базиса с коэффициентом, равным 1 (t).

Введение такой искусственной переменной позволяет нам взять точку в начале координат, но эта точка не входит в область допустимых решений. Переменная искусственного базиса является стартом для решения задачи симплекс-методом, в процессе решения она выходит из базиса и становится равной 0.

В целевую функцию переменная искусственного базиса записывается с коэффициентом М и вычитается из целевой функции. М – это очень большое число, которое, если t не равняется нулю, не позволяет функции принять максимальное значение.

.

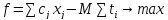Т.е. если t не равно нулю, то значение функции только уменьшается.

Алгоритм решения:

Если после введения балансовой переменной в матрице системы ограничений нет достаточного количества столбцов, из которых можно составить единичную матрицу, то в те уравнения, которые не содержат базисной переменной, вводится искусственная переменная t, в каждое своя.

Искусственные переменные вводятся в целевую функцию с положительным большим коэффициентом М со знаком «-» (коэффициент М – одинаков для всех t).

Рассмотрим 2 задачи:

задача 1	задача 2

Т.е. в первой задаче у нас уже введены балансовые переменные, но не хватает столбцов, из которых можно сделать единичную матрицу. Поэтому мы преобразуем эту задачу в задачу 2, добавляя искусственную переменную. Далее решаем задачу обычным симплекс методом.

1. Если задача 2 имеет оптимальное решение вида , т.е. все искусственные переменные равны нулю, то 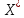- оптимальное решение задачи

2. Если при решении задачи 2 получено оптимальное решение вида 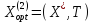, т.е. Т не равно 0, то область допустимых решений задачи 1 пуста.

3. Если при решении задачи 2 получено решение вида , т.е. решение неоптимальное (существует отрицательная оценка, но в разрешающем столбце нет положительных коэффициентов), то в задаче 1 целевая функция неограниченно растет.

4. Если при решении задачи 2 получено решение вида , т.е. t не равно 0, решение неоптимальное (существует отрицательная оценка, но в разрешающем столбце нет положительных коэффициентов), то в задаче 1 область допустимых решений пуста.

После введения искусственных переменных, они становятся базисными, а в таблице появляется дополнительная строка – М. На первом этапе оценки М-строки всех переменных кроме искусственных равны 0. Оценка при искусственных переменных равна 1.

Оценки в строке целевой функции записываются со знаком +.

Далее следует вычеркнуть эту М-строку и составить новую, чтобы иметь возможность начать решение симплекс-методом (на первом этапе это невозможно из-за отсутствия отрицательных оценок).

Для того, чтобы получить новую М-строку, нужно все искусственные переменные умножить на -1 и прибавить к старой М-строке.

Дальнейшее решение идет как обычно: выбирается разрешающий столбец, строка, элемент, ведется пересчет.

В последней таблице получаем М-строку как в начале: все оценки равны 0 кроме оценок при искусственных переменных.

Значение целевой функции в столбце свободных переменных получается отрицательным, ответ (оптимальное значение функции) берется без знака минус.

Можно решать, не вводя в таблицу дополнительную М-строку. Можно из ограничений, содержащих искусственные переменные t, выразить эти t и подставить выражения в целевую функцию. Затем раскрыть скобки и привести подобные слагаемые. Далее решать как обычно (в оценках в строке целевой функции будут числа с М).

12. Задача, двойственная данной (Случаи ограничений, заданных в виде неравенств и равенств; случаи неотрицательных переменных и переменных любого знака).

Задача, двойственная данной, строится по определению следующим образом:

1. Если прямая задача на максимум, то двойственная – на минимум.

2. Если задача на максимум, то ограничения либо в сторону меньше, либо равенства. Соответственно и наоборот: если задача на минимум, то ограничения в сторону больше, либо равенства.

3. Число переменных двойственной задачи равняется числу ограничений прямой.

4. Число ограничений двойственной задачи равняется числу переменных прямой.

5. Матрицы ограничений прямой и двойственной задачи транспонированы относительно друг друга.

6. Чтобы составить двойственную задачу каждому ограничению прямой задачи сопоставляют переменную двойственной.

7. Коэффициент целевой функции двойственной задачи равен правым частям ограничений прямой задачи (.

8. Правые части ограничений двойственной задачи совпадают с коэффициентами целевой функции прямой задачи.

9. Если ограничение задано в виде неравенства, то двойственная переменная неотрицательна.

10. Если ограничение задано в виде равенства, то двойственная переменная может принимать любые значения.

11. Если переменная прямой задачи неотрицательна, то ограничение двойственной заданы в виде неравенства.

12. Если переменная прямой задачи может принимать любые значения, то соответствующее ограничение двойственной задано в виде равенства.

Задача, двойственная двойственной, является прямой.

Доказательство:

Рассмотрим две задачи: прямую и двойственную:

Прямая задача	Двойственная задача

В данный момент работаем с двойственной. Нужно сделать из нее задачу на максимум с ограничениями в сторону меньше (стандартная форма). Введем новое обозначение для целевой функции этой задачи: g*.

Для приведения задачи к новому виду домножим целевую функцию и ограничения на -1.

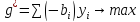
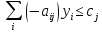
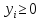
Теперь составим для новой задачи двойственную, целевую функцию которой обозначим f*. Пусть для этой двойственной задачи будет :

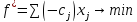
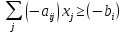
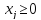
Теперь перепишем данную задачу как задачу на максимум. Обозначим целевую функцию f:

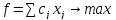
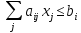
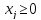
Таким образом, мы получили изначальную задачу. Теорема доказана.