1. Формулировка задачи линейного программирования (злп) в общей (озлп), стандартной (сзлп) и канонической (кзлп) формах. Переход от одной формы записи к другой

Математическое программирование — область математики, разрабатывающая теорию и численные методы решения задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных.

Функцию, экстремальное значение которой нужно найти в условиях экономических возможностей, называют целевой, показателем эффективности или критерием оптимальности. Экономические возможности формализуются в виде системы ограничений. Все это составляет математическую модель. Математическая модель задачи — это отражение оригинала в виде функций, уравнений, неравенств, цифр и т. д. Модель задачи математического программирования включает:

1) совокупность неизвестных величин, действуя на которые, систему можно совершенствовать. Их называют планом задачи (решением, стратегией, поведением игрока и др.);

2) целевую функцию (функцию цели, показатель эффективности, критерий оптимальности, функционал задачи и др.). Целевая функция позволяет выбирать наилучший вариант из множества возможных. Наилучший вариант доставляет целевой функции экстремальное значение. Это может быть прибыль, объем выпуска или реализации, издержки и т.д.

Эти условия следуют из ограниченности ресурсов, которыми располагает общество в любой момент времени, из необходимости удовлетворения потребностей, из условий производственных и технологических процессов. Математически ограничения выражаются в виде уравнений и неравенств.

1. Общая задача линейного программирования:

Задана система ограничений

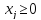(ограничения могут быть в любую сторону).

И целевая функция

Требуется среди неотрицательных решений системы ограничений найти такое решение (вектор) 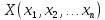, чтобы значение целевой функции было максимальным (минимальным).

2. Стандартная задача линейного программирования:

Задана система ограничений в сторону меньше или равно (для задачи на максимум) и больше или равно (для задачи на минимум).

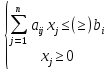
И целевая функция .

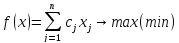Требуется среди неотрицательных решений системы ограничений найти такое решение (вектор) , чтобы значение целевой функции было максимальным (минимальным).

3. Каноническая форма задачи линейного программирования:

Задана система ограничений в виде равенств

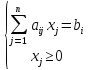
И целевая функция .

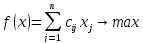Требуется среди неотрицательных решений системы ограничений найти такое решение (вектор) 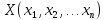, чтобы значение целевой функции было максимальным.

Также существует приведенная каноническая форма, в которой система ограничений может быть записана в матричной форме:

.

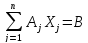При этом ранг матрицы А равен числу уравнений. Среди столбцов матрицы А должны быть столбцы, из которых можно составить единичную матрицу соответствующего порядка.

Для решения задачи линейного программирования её нужно записать в приведенной канонической форме, в некоторых ситуациях – в стандартной. Поэтому возникает потребность переходить от одной формы задачи к другим:

1. Задачу на минимум переписать в задачу на максимум, домножив целевую функцию на -1.

.

.

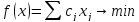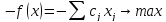2. Стандартная форма требует ограничений в сторону меньше, но имеется одно из ограничений в сторону больше. Необходимо домножить это ограничение на -1.

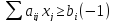
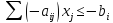
3. Если ограничения заданы в виде равенств, нужна стандартная форма, то их можно расписать в виде системы двух неравенств:

. Соответственно дальше домножим первое неравенство на -1, чтобы получить оба ограничения в сторону меньше: .

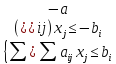4. Если величина любого знака, а для стандартной формы требуется неотрицательная величина, то необходимо x представить в виде разности двух неотрицательных величин и подставить эти величины в целевую функцию и ограничения: .

.

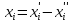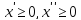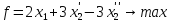
5. Требуется перейти из неравенства в равенство.

При приведении к канонической форме нужно вводить дополнительные (балансовые) переменные. В каждое ограничение записывается своя балансовая переменная, соответственно их столько же, сколько ограничений. Балансовые переменные обязательно неотрицательные.

С их помощью можно уравнять как ограничение в сторону меньше, так и ограничения в сторону больше. В первом случае балансовая переменная прибавляются к ограничению, во втором – отнимается.

;

.

;

.

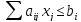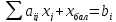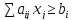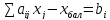Балансовые переменные записываются в целевую функцию с нулевым коэффициентом. Добавление балансовой переменной не влияет на значение х.

6. Иногда встречаются задачи, в которых добавляется какой-то числовой коэффициент c. Тогда решаем с переменными, а потом добавим это число с. То есть нужно перейти к функции, которая меньше на это число с, решить задачу и прибавить к ответу это число.

.

.

.

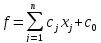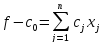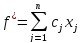2. Примеры ЗЛП: задача производственного планирования, задача оптимизации рациона питания (задача о диете)

Задача производственного планирования:

Даны несколько видов изделия. Также даны несколько типов ресурсов, требующихся для производства этих изделий. На каждое изделие расходуется определенное количество сырья. Необходимо составить план выпуска изделий, чтобы получить наибольшую выручку при заданных ценах.

Числовой пример:

Предприятие производит 2 вида изделия, для производства которых требуется 3 типа ресурса:

Ресурса А на складе имеется 18 единиц,

ресурса В – 37 единиц,

ресурса С – 24 единицы.

Расход сырья для производства первого изделия: типа А – 1 единица, типа В – 4 единицы, типа С – 3 единицы.

Расход сырья для производства второго изделия: 2, 3, 1 единицы соответственно.

Составить план выпуска изделий для получения наибольшей выручки при заданных ценах на изделия: цена первого изделия =2, цена второго =3.

Можно составить таблицу для наглядности:

	1 изделие	2 изделие	запасы сырья
ресурс А	1	2	18
ресурс В	4	3	37
ресурс С	3	1	24
Цена	2	3

Тогда требуемый вектор 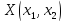, где 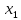– количество изделий первого вида, 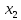– количество изделий второго вида.

Система ограничений составляется для сырья (мы не можем использовать для производства больше, чем у нас имеется), и в данном случае выглядит следующим образом:

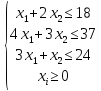
Целевая функция (наша выручка) строится следующим образом: 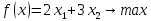. Т.е. цена первого изделия на количество изделий первого вида плюс цена второго изделия на количество изделий второго вида.

Задача оптимизации рациона питания (задача о диете):

Даны несколько типов кормов (продуктов), каждый из которых содержит определенное количество питательных веществ. Необходимо получить определенное количество (не менее скольки-то) питательных веществ, чтобы затраты были минимальными при заданных ценах на корм (продукт).

Числовой пример:

В наличии имеется 2 вида продукта, каждый из которых содержит три вида питательных веществ.

В первом продукте содержится 1 единица питательного вещества 1, 4 единицы питательного вещества 2 и 3 единицы питательного вещества 3.

Во втором продукте – 2, 3, 1 единица соответственно

Для составления оптимального рациона питания необходимо получать не менее 18 единиц питательного вещества первого вида, не менее 37 – второго вида, не менее 24 – третьего вида.

Необходимо составить оптимальный рацион питания, чтобы затраты при этом были минимальны.

Тут также можно составить таблицу

	Продукт 1	Продукт 2	минимально необходимое количество питательных веществ
питательное вещество 1	1	2	18
питательное вещество 2	4	3	37
питательное вещество 3	3	1	24
Цена	2	3

Тогда требуемый вектор 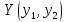, где 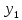– количество продукта первого вида, 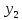– количество продукта второго вида.

Система ограничений составляется для питательных веществ (мы не можем потреблять меньше, чем организму необходимо), и в данном случае выглядит следующим образом:

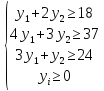
Целевая функция (затраты на данный рацион) выглядит следующим образом: .

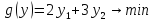3. Определения допустимого, базисного, оптимального решений ЗЛП

При решении задач линейного программирования бывают:

1. Допустимые решения (допустимый план) – такой набор 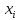, который удовлетворяет системе ограничений.

2. Базисное решение (план) – допустимое решение, в котором все свободные переменные равны нулю, а все базисные неотрицательные (т.е. задача в канонической форме). Всегда достигается в вершинах области.

3. Оптимальное решение (план) – решение, на котором функция достигает своего оптимального значения (т.е. максимума или минимума, в зависимости от условия задачи). Оптимальное решение также является допустимым. Оптимальное решение всегда базисное (см. билеты 6-9).

4. Графический метод решения ЗЛП. Определение линии уровня. Роль градиента линейной функции в графическом методе

Графический метод решения применим тогда, когда в задаче имеются две переменные (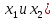. Для применения этого метода необходимо вспомнить, что такое линия уровня и градиент.

Линия уровня – множество всех тех точек плоскости, которые удовлетворяют равенству f(x,y)=c.

Градиент – вектор, координатами которого являются частные производные.

Также помним, что градиент обладает двумя свойствами:

1. Он перпендикулярен линии уровня;

2. Он показывает направление наибольшего возрастания функции.

Насчет второго свойства стоит пояснить: Если дана линейная функция и l1, l2, l3 – ее линии уровня, которым соответствуют значения функции f1, f2, f3, то если при перемещении линии l1 параллельно самой себе по направлению градиента, получаем линии l2, а потом l3, то можно составить соотношение между значениями функций: f1<f2<f3.

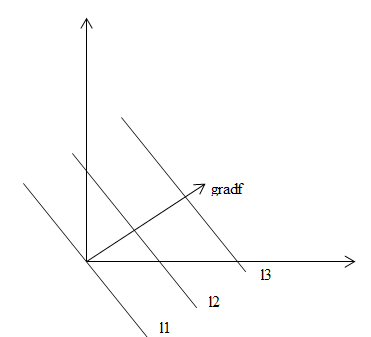
Справедливо и обратное: зная соотношение между функциями можно узнать расположение линий уровня.

Графический метод решения ЗЛП построен на этом свойстве. Для того, чтобы решить задачу данным методом, необходимо:

1. построить прямые, соответствующие неравенствам ограничений, определить полуплоскости, соответствующие указанным ограничениям, найти область пересечения указанных полуплоскостей. Эта область будет являться областью допустимых решений (допустимых планов).

Для того, чтобы определить, нужная ли это полуплоскость, выбираем любую точку на графике (не на самих линиях). Если подставить координаты этой точки в неравенство, и оно выполняется, то с этой полуплоскостью и работаем.

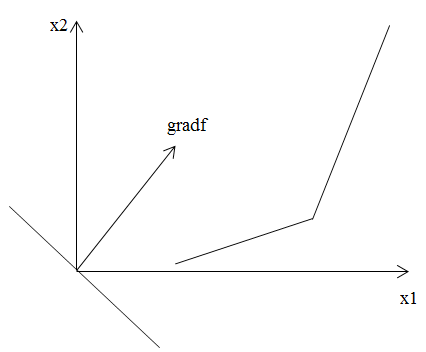
2. Нарисовать вектор градиента целевой функции и перпендикулярно ему линию уровня целевой функции. Если она проходит через начало координат, то она соответствует f=0.

Так как функции, которые мы рассматриваем, линейные, то вектором градиента будут коэффициенты перед x.

3. Перемещать линию уровня параллельно самой себе до крайней точки области, исходя из условия задачи (максимум или минимум нужно найти?)

4. Найти координаты данной крайней точки области, решив соответствующую систему уравнений (уравнения отвечают линиям, которые пересекаются в данной точке).

5. Найти значение функции в указанной точке.

Замечания:

1. Если целевая функция имеет постоянное значение, то линия уровня при проходит через с.

;

.

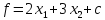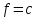2. При параллельном перемещении линии уровня можно прийти не к крайней точки области, а к отрезку (см. билет 5).

3. Если ограничение задано в виде равенства, то область допустимых решений – отрезок этой прямой.

Отрезком называется такое множество точек, координаты которого удовлетворяют равенству: 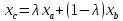, где λ принимает значения от 0 до 1.

5. Возможные варианты решения ЗЛП: единственное оптимальное решение, отсутствие допустимых решений, неограниченное значение целевой функции, альтернативное решение, вырожденное решение (графическая иллюстрация)

1. Единственное оптимальное решение

При перемещении линии уровня параллельно самой себе по направлению вектора градиента, приходим в крайнюю точку области, отвечающую условиям задачи (если функция на минимум, то первая точка «на пути», если функция на максимум, то самая дальняя точка области). Соответственно, находится одна оптимальная точка, которая и будет являться ответом.

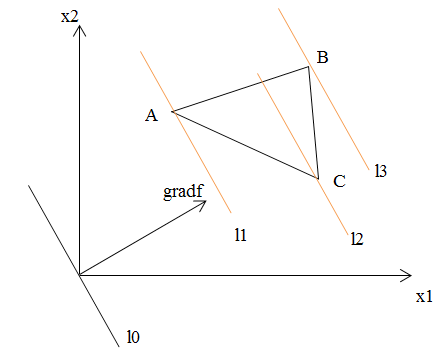
На рисунке оптимальной точкой, если функция на максимум, будет являться точка В (до нее дольше всего «идти»), а если функция на минимум, то точка А (она, наоборот, находится ближе всего).

2. Отсутствие решений

Тут возможны два варианта:

а) либо область допустимых решений пуста (полуплоскости не пересекаются друг с другом)

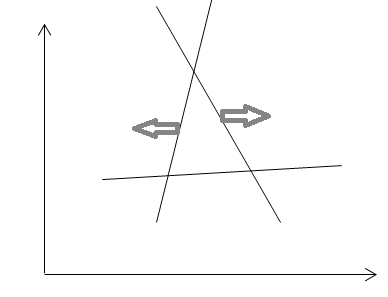
б) либо целевая функция неограниченно растет (при условии, что задача на максимум).

В этом случае мы просто не можем определить оптимальную точку, потому что область не ограничена сверху.

Однако если задача на минимум, то оптимальную точку найти можно, как и в варианте с единственным решением: оптимальной будет являться та точка, которая первой встретится на пути.

3. Альтернативное решение

Если отрезок области допустимых планов расположен параллельно линии уровня, то существуют альтернативные решения: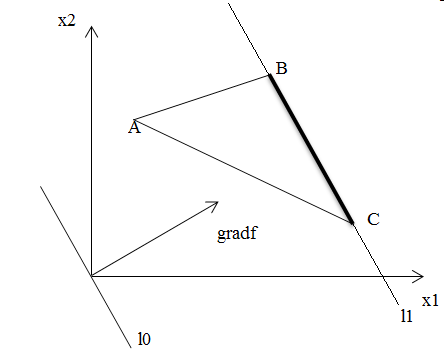

Т.е. оптимальной может являться как точка В, так и точка С, и все множество точек между ними (потому что все они встретятся на пути линии уровня одновременно).

Ответом в таком случае будет являться отрезок.

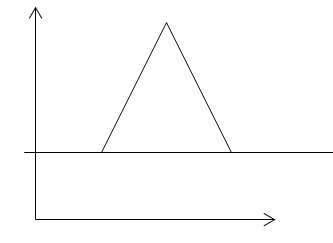
4. Вырожденное решение

Одна из базисных переменных в оптимальной точке равна нулю. Графически это означает, что в точке пересекаются более двух прямых, одна из этих прямых является лишней (не влияет на вид области допустимых планов).

На данном рисунке l2 является, в общем-то, лишней прямой, потому что форма области допустимых решений и оптимальная точка никак не зависят от нее.

6. Теорема о виде области допустимых решений КЗЛП.

Если область допустимых решений ЗЛП не пуста, то это выпуклый многогранник.

Область называется выпуклой, если вместе с любыми двумя точками она содержит весь отрезок.

Отрезок AB – такое множеств точек, координаты которых удовлетворяют равенству , λ меняется от 0 до 1.

То есть, если мы решим, например, расширить или продлить этот треугольник, он все равно весь останется с одной стороны этой линии.

То, что область является многогранником, можно доказать из линейных ограничений.

Доказательство того, что область допустимых решений выпукла:

Пусть заданы ограничения ЗЛП:

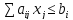. Пусть точки 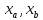принадлежат допустимой области.

То есть:

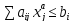
Домножим первое неравенство на λ, второе – на 1-λ:

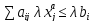
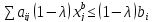
Сложим эти два неравенства:

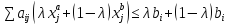
В левой части в скобках написано представление точки на отрезке, как комбинации его вершин, поэтому обозначим эту скобку как точку .

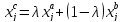В правой же части раскрываем скобки и получаем просто 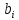. Перепишем неравенство:

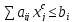,т.е. получаем, что любая точка области отвечает этим ограничениям (кроме 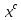можно взять любую другую точку).

Раз любая точка области отвечает этим ограничениям, то область является выпуклой (т.к. любая выпуклая комбинация точек, принадлежащих выпуклому множеству, также принадлежит этому множеству).

7. Теорема о допустимых и базисных решениях КЗЛП

Базисным называется решение, в котором свободные переменные равны нулю, а базисные – неотрицательны.

Задача задана в канонической форме, если из ограничений можно составить единичную матрицу.

Теорема: Если в задаче линейного программирования имеется допустимое решение, то в канонической форме существуют базисные решения.

8. Теорема о базисном решении КЗЛП и вершине области.

Точка Х является вершиной выпуклого многогранника, если не существует двух различных и не совпадающих с точкой Х точек данного многогранника, таких, что выполняется равенство:

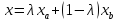
Т.е. точка является вершиной, если она не является внутренней точкой отрезка, концы которого целиком принадлежат многограннику.

Если какая-то точка является вершиной области, то в ней – базисное решение.

Теорема: для того, чтобы точка Х была вершиной области допустимых решений задачи линейного программирования, необходимо и достаточно, чтобы Х являлась базисным решением канонической базисной формы задачи.

Необходимо: Дано: Х – вершина; доказать: Х – базисное решение. Без доказательства.

Достаточно: Дано: Х – базисное решение; доказать: Х – вершина.

Доказательство от противного:

Предположим, что точка Х не является вершиной, следовательно, она может быть представлена в виде комбинации двух других точек (А и В):

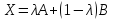, где 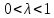(λ не может принимать крайние значения 0 и 1, т.к. мы предположили, что точка Х – внутренняя).

По определению базисного решения свободные переменные в нем равны нулю, а базисные переменные не отрицательны. Так же известно, что базисных переменных столько, каков ранг матрицы.

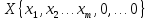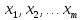Т.к. нам дано, что Х является базисным решением, то эта точка имеет структуру: , где m –ранг матрицы (т.е. являются базисными переменными, а .

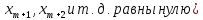Если мы предположили, что Х – не вершина, то для любых переменных можно записать равенство 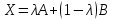. Запишем его для свободных переменных:

;

;

;

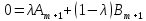А и В не являются отрицательными, потому что задача дана в канонической форме. Как и говорилось выше, λ не равна 0 и не равна 1, потому что Х – внутренняя точка.

Но сумма двух положительных чисел никак не может равняться нулю, следовательно и А и В равны нулю для свободных переменных (от m+1 до n).

Поэтому А и В имеют структуру:

;

.

Как мы видим, Х, А и В имеют одну структуру, то есть Х нельзя представить в виде комбинации А и В. Следовательно, Х является вершиной по определению.

Векторная форма записи: 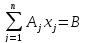, где – линейное разложение вектора В по системе линейно независимых векторов. Если такое разложение единственно, то Х – вершина.