13. Теорема о связи оптимальных значений функций прямой и двойственной задач.

Нужная теорема является следствием к данной, поэтому её тоже придется рассмотреть.

(теорема о неравенстве целевых функций) На области допустимых планов значение целевой функции задачи на максимум не превосходит значения целевой функции задачи на минимум.

Т.е. .

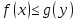Доказательство:

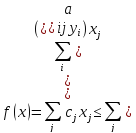
Постараюсь объяснить.

Пусть дана прямая задача:

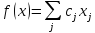
Так как является в то же время правой частью ограничения двойственной задачи (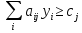), то мы можем домножить обе части этого ограничения на 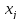и просуммировать по столбцам (сумма по j), чтобы получить в правой части неравенства целевую функцию f.

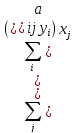
По правилам мы можем менять порядок сумм, что и сделаем. Также поменяем местами у и х в левой части неравенства (от перестановки мест множителей произведение не меняется, как известно). Получим следующее:

Вид маленькой скобки должен напомнить нам левую часть ограничения прямой задачи (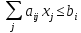). Как мы видим, у нас эта левая часть еще домножена на у и просуммирована по строкам (сумма по i). Соответственно и правую часть этого ограничения приведем к тому же виду:

А эта правая часть является целевой функцией g двойственной задачи (.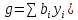

Таким образом, исключив промежуточные действия по преобразованию выражений, получим, что 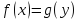, что и требовалось доказать.

Из данной теоремы выводится следствие:

Если известно, что 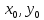являются допустимыми решениями прямой и двойственной задачи, и известно, что значение целевых функций в данных точках совпадает (), то 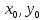– оптимальные решения.

Доказательство от противного:

Пусть нам дана задача на максимум. Допустим, что 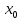не является оптимальным решением этой задачи, но существует какое-то другое оптимальное решение – Х*.

Тогда значение целевой функции в оптимальной точке должно быть больше, чем в других точках. Т.е. получаем, что .

По условию нам дано, что значения функций прямой и двойственной задач совпадают в заданных точках (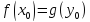). Подставим g вместо f в неравенство выше:

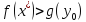
Однако это противоречит предыдущей теореме (значение целевой функции задачи на максимум не превосходит значения целевой функции задачи на минимум).

14. Признак отсутствия допустимого решения для задачи двойственной данной.

Также является следствием из предыдущей теоремы.

Если целевая функция задачи на максимум неограниченно возрастает, то область допустимых решений двойственной задачи пуста.

Предположим, что существует допустимое решение двойственной задачи (У*)

Если мы подставим эту точку в целевую функцию, то получим какое-то число.

Соответственно, это число должно быть больше любого значения целевой функции задачи на максимум (см. билет 13) (.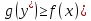

Но целевая функция прямой задачи на максимум по условию неограниченно растет, следовательно, не существует такого допустимого решения У*, т.е. область допустимых решений пуста.

15. Теорема о связи оптимальных решений прямой и двойственной задач (Первая теорема двойственности).

Если прямая задача имеет оптимальное решение, то и двойственная тоже имеет оптимальное решение, причем значения целевых функций совпадают.

Замечание:

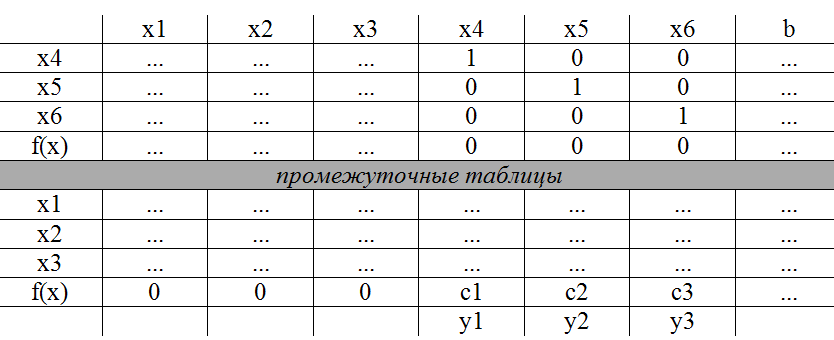
Если исходная задача имела стандартную форму (функция на максимум, все ограничения были в сторону меньше, а все переменные неотрицательны), то ответ к двойственной задаче можно увидеть в последней таблице в индексной строке в столбцах балансовых переменных.

Оценки в индексной строке в последней таблице, стоящие в тех столбцах, которые соответствуют базисным переменным в исходной таблице, являются двойственными оценками, они же – решения двойственной задачи.

Так же наоборот.

16. Необходимое и достаточное условие существования оптимальных решений прямой и двойственной задач (Вторая теорема двойственности).

Для того, чтобы являлись оптимальными решениями прямой и двойственной задач, необходимо и достаточно, чтобы выполнялись условия:

1. Если какая-то переменная одной из задач на оптимальном решении строго положительна, то соответствующее ограничение двойственной на оптимальном решении выполняется в виде равенства.

2. Если какое-то ограничение одной из задач выполняется как строгое неравенство, то соответствующая переменная двойственной задачи на оптимальном решении равна 0.

Т.е. должны выполняться 4 условия:

1.

2.

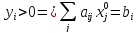
3. .

4.

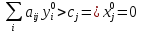
Доказательство:

Вернемся к цепочке из теоремы в 13 билете:

Данная цепочка справедлива всегда, но на оптимальном решении все нестрогие неравенства выполняются как равенства (это следует из первой теоремы двойственности: ).

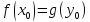Рассмотрим эту часть цепочки: 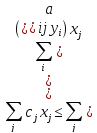, заменив знак на равно. Перенесем все в левую часть, чтобы справа остался 0.

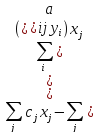
Теперь можно вынести за скобку общий знак суммы (по столбцам) и общий множитель 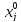. Также умножим на -1, чтобы поменять местами части выражения.

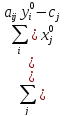
Скобка неотрицательна (это ограничение двойственной задачи 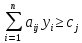), переменная неотрицательна по определению. Следовательно, их произведение также неотрицательно. То есть получается, что все слагаемые неотрицательны, а их сумма равна 0. Следовательно, все слагаемые равны 0:

Чтобы произведение равнялось 0, нужно чтобы хотя бы один их множителей равнялся 0. Следовательно, если скобка положительна, то переменная равна 0 (4 условие). Если же переменная положительна, то 0 равна скобка (1 условие).

2 и 3 условие повторяют 1 и 4, но для двойственной задачи.

Замечания:

1. Может быть вариант, когда ограничения выполняются в виде равенств и переменная равна 0. Это признак вырожденного решения.

Если решение исходной задачи вырожденное, то требуются дополнительные рассуждения: 2 случая (строгое неравенство или равенство).

Если у одной задачи есть альтернативное решение, то у другой – вырожденное, если альтернативное решение первой задачи не вырожденное.

2. Поскольку на оптимальном решении значения функций совпадают, то если рассматривать задачу производственного планирования, где задаются ограничения на сырье (правые части ограничений – запасы сырья), то двойственные оценки прямой задачи показывают, насколько изменится значение целевой функции при изменении запасов сырья на единицу.

3. Задача, когда целевая функция на минимум, а все ограничения в сторону больше или равно, переменные неотрицательные – задача о диете (билет 2). По своей структуре она двойственна задаче производственного планирования.

4. Если дана задача типа «о диете» и для ее решения требуется введение искусственных переменных, то можно перейти к задаче типа производственного планирования, решить ее и, тем самым, узнать ответ к исходной задаче.

5. Если дана задача, к которой известен ответ, то можно найти ответ и к двойственной задаче, пользуясь условиями из второй теоремы двойственности.

17. Анализ на чувствительность.

Задача имеет такие параметры как запасы сырья (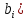, цена изделия (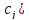. Анализ на чувствительность предполагает изменение одного параметра таким образом, чтобы сохранились базисные переменные последней таблицы, и выяснение того, как изменится результат.

Анализ на чувствительность предполагает ответы на следующие вопросы:

1. Насколько можно уменьшить запас недефицитного ресурса, чтобы оптимальная точка осталась прежней?

Тот ресурс, который не расходуется полностью, называется недефицитный. Если ресурс израсходован полностью, то дефицитный.

2. Как изменится результат, если увеличить запас какого-либо дефицитного ресурса?

3. Насколько можно изменить цену одного изделия, чтобы оптимальная точка осталась прежней?

4. Как изменить цены, чтобы оптимальной стала «соседняя» точка? (т.е. как изменить вектор градиента).

Анализ можно проводить как графически, так и с помощью таблицы.

Графический способ:

1. Ограничения в задаче накладываются на ресурсы. Оптимальная точка – точка пересечения двух каких-то прямых (значит ресурсы, соответствующие этим прямым, расходуются полностью). Поэтому чтобы узнать, насколько можно уменьшить запасы недефицитного ресурса (прямая, которая не проходит через оптимальную точку), нужно сместить эту прямую параллельно самой себе так, чтобы она проходила через оптимальную точку.

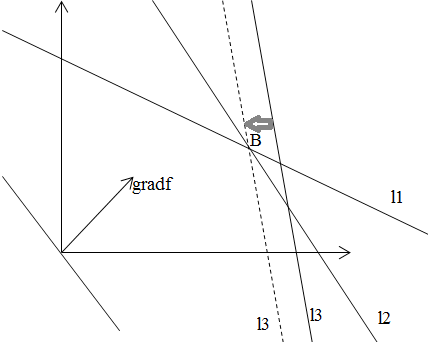
Далее подставляем координаты оптимальной точки в ограничение, соответствующее данной прямой.

На данном графике недефицитный ресурс – l3, а оптимальная точка – В.

2. Для ответа на второй вопрос, введем понятие ценности ресурс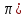а ( – насколько изменится целевая функции при изменении ресурса.

, где n – номер ресурса в задаче.

Для недефицитных ресурсов ценность равна 0 (их количество можно только уменьшать, а ещё больше наращивать бессмысленно).

Дефицитные же ресурсы наращивать можно.

Чтобы узнать, до какого уровня можно нарастить тот или иной ресурс, нужно посмотреть на графике, до какой точки можно переместить вправо параллельно самой себе прямую, соответствующую ограничению на данный ресурс.

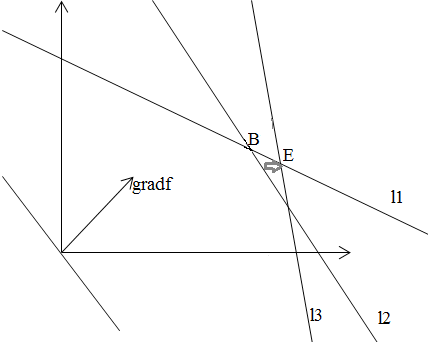
Далее подставляем координаты новой оптимальной точки в ограничение и в целевую функцию. Ищем разницу между новыми и старыми значениями и подставляем в формулу выше.

На графике мы можем нарастить ресурс l2 до точки Е (т.к. она находится правее точки В).

Возвращаясь к двойственной задаче – смысл двойственных переменных – ценность ресурсов ( и т.д.