4.2. Разложение вектора по ортам. Модуль вектора

1⁰.Разложение вектора по ортам. Из прямоугольного параллелепипеда (рис. 4.1) следует:

.

Но ,,,, Следовательно,

(4.3)

Равенство (4.3) и есть формула разложения вектора по ортам координатных осей.

Таким образом, координатная запись вектора может быть осуществлена двумя способами:

2⁰.Модуль вектора. Векторявляется диагональю прямоугольного параллелепипеда (рис. 4.1). Квадрат длины диагонали равен сумме квадратов трех его измерений:

,

отсюда следует: , и наконец, получаем искомую формулу:

(4.4)

Модуль вектора равен корню квадратному из суммы квадратов его координат.

4.3. Линейные операции над векторами.

Сформулируем правила действийнад векторами в координатной форме.

.Координаты суммы (разности) векторов равны суммам (разностям) соответствующих координат этих векторов.

Пусть тогда

(4.5)

При умножении вектора на скаляр его координаты умножаются на этот скаляр.

Если и– скалярная величина, то

(4.6)

Покажем применение рассмотренного в этой главе материала к решению практической задачи.

Задача 4.1. Даны векторы:

Найти: координаты и модуль вектора

Решение.Используем координатную запись векторов и правила линейных операций над ними:

Модуль вектора вычислим по формуле (4.4):

Ответ.

4.4. Направляющие косинусы вектора

О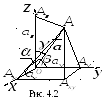пределение 4.2. Направляющими косинусами ненулевого вектора называются косинусы углов, которые этот вектор образуют с осями координат (рис. 4.2).

Выразим координаты вектора через его модуль и углы:

С помощью данных равенств найдем выражения направляющих косинусов через координаты вектора и его модуль:

(4.7)

Вычислим сумму квадратов направляющих косинусов вектора :

Полученный результат в векторной алгебре сформулирован в виде следующего утверждения:

Сумма квадратов направляющих косинусов ненулевого вектора равна единице:

(4.8)

Задача 4.2.Определить направляющие косинусы вектора а также убедиться в справедливости тождества(4.8).

Решение.1⁰. Определим координаты и модуль вектора:

2⁰. Вычислим направляющие косинусы вектора

3⁰. Проверим справедливость тождества (4.8):

Ответ.

4.5. Координаты точки в пространстве. Вычисление координат вектора и его модуля по координатам его начала и конца.

Введем понятие координат точки в пространстве через понятие радиус-вектора.

Определение 4.3. Радиус-вектором точки М называется вектор с началом в начале координат и концом в точке М, то есть вектор (рис. 4.3).

В качестве координат точки М примем координаты радиус-вектора.

Определение 4.4. Координатами точки в пространстве называются координаты ее радиус-вектора.

Координаты точки М (рис. 4.3) обозначаются символом:, или. Таким образом,

Поставим задачу:найти координаты и модуль вектора , если известны координаты его начала и конца: (рис. 4.4).

Решение.Проведем в точкиАиВ радиус-векторыи, выразим координаты векторачерез координаты векторови(см. определение 4.4), получим:

(4.9)

Координаты вектора равны соответствующим разностям координат конца и начала этого вектора.

Задача 4.3.Даны две точки: Найти координаты, разложение по ортам координатных осей, модуль и направляющие косинусы вектора

Решение.Для определения координат векторавоспользуемся формулой (4.9):

По формуле (4.4) вычислим модуль вектора :

Найдем направляющие косинусы вектора :

Вычислим сумму квадратов направляющих косинусов:

Ответ.