2. Линейные операции над векторами

К линейным операциям над векторами относятся следующие операции:

• сложение векторов;

• вычитание векторов;

• умножение вектора на скаляр (действительное число).

2.1 Сложение векторов

Определение 2.1. Суммой двух векторов называется третий векторимеющий своим началом начало вектора, а концом – конец векторапри условии, что начало векторасовпадает с концом вектора(векторприведен к концу вектора)(рис. 2.1).

Это определение сложения двух векторов носит название «правило треугольника.

Это правило сложения векторов можно распространить на любое их количество.

Правило. Чтобы сложить любое количество векторов, следует расположить их так, чтобы конец каждого предыдущего вектора был началом следующего и построить вектор началом в начале первого и концом в конце последнего вектора(рис. 2.2).

Наряду с правилом треугольника сложения векторов существует «правило параллелограмма»

Определение 2.1^*. Суммой векторов иявляется вектор– вектор-диагональ параллелограмма, построенного на векторахи, причем векторыиприведены к одному началу(рис. 2.3).

На рис 2.3 этой диагональю является диагональ .

По правилу параллелограмма определяется равнодействующая двух сил. Для нахождения равнодействующей сили,, приводим эти силы к точкеи строим на них параллелограмм. Вектор-диагональпараллелограмма и является равнодействующих этих сил (рис. 2.4).

Свойства сложения векторов

–коммутативный (переместительный) закон.

Рис. 2.3 иллюстрирует справедливость свойства. В самом деле:

‑ассоциативный (сочетательный) закон.

для любого вектора .

Для любого вектора : .

2.2 Вычитание векторов

Определение 2.2. Разностью двух векторов иназывается третий вектор, такой, что.

Покажем, как реализуется на практике сформулированное определение понятия разности.

Задача 2.1. Даны два вектора:

Найти: разность векторов и.

Решение.Приведем варианта два решения.

1⁰. Из определения следует: чтобы построить разность двух векторовэти векторы надо привести к одному началу, а затем построить вектор с началом в конце вектораи концом в конце вектора(рис. 2.5). Суммой векторовиявляется вектор .

Обратимся к рис. 2.3. В параллелограмме OACB диагональOC является суммой векторови, а диагональBA – разностью этих векторов.

2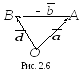⁰. Преобразуем равенство . Следовательно, векторявляется суммой вектораи вектора, противоположного вектору. Отсюда следует построение искомой разности векторов (рис. 2.6).

2.3. Умножение вектора на скаляр

Определение 2.3. Произведением вектора на скалярназывается вектор , удовлетворяющий двум условиям:

• модуль вектора равен произведению модулей числа и вектора: ;

• вектор сонаправлен с векторомприи направлен противоположно векторупри(рис. 2.7).

Свойства умножения вектора на скаляр

.;

.;

. ассоциативный (сочетательный) закон по отношению к скалярным множителям;

. – дистрибутивный (распределительный) закон по отношению к векторному множителю;

. – дистрибутивный (распределительный) закон по отношению к числовому множителю.

Замечание. Свойства сложения векторов и умножения вектора на число свидетельствуют о следующем: векторные одночлены и многочлены можно преобразовывать относительно этих операций по правилам преобразования алгебраических одночленов и многочленов.

В заключение рассмотрим пример использования изученных свойств на практике.

Задача 2.2.Даны два вектора и:

Найти: вектор .

Решение.Преобразуем выражение вектора, используя свойства сложения векторов и умножения вектора на скаляр:

Полученную сумму построим по правилу треугольника (рис. 2.8).