
- •6.4.1 Оцінка автентичності захисту інформації з використанням симетричних алгоритмів. Приклади розв’язку задач та задачі для самостійного розв’язання
- •Ми застосуємо в оцінці відповідне більше, так як не доведено, що в режимі виробки імітоприкладки забезпечується досконала автентичність.
- •1.12 Оцінка автентичності інформації, захищеної з використанням асиметричних алгоритмів. Приклади розв’язку задач та задачі для самостійного розв’язання
- •Відомо також, що імовірність обману можна визначити як
- •1.13 Криптоаналіз rsa та дискретних логарифмiв методом -Поларда. Приклади розв’язку задач та задачі для самостійного розв’язання
- •Задача 1.
- •1.14 Криптоаналiз rsa методом квадратичного решета. Приклади розв’язку задач та задачі для самостійного розв’язання
- •Задача 1.
- •2.7 Аналіз методiв перетворень в перспективних симетричних криптографічних системах. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.9 Симетричні потокові шифри. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.9.1 Приклади розв’язку задач
- •2.10 Стійкість асиметричних криптосистем, що базуються на криптоперетвореннях в простих полях. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.11 Стійкість асиметричних криптосистем, що базуються на криптоперетвореннях в групі точок еліптичних кривих. Приклади розв’язку задач та задачі для самостійного розв’язання
- •Використовуючи формули для додавання точок:
- •При подвоєнні маємо:
- •2.12 Електронні цифрові підписи та їх застосування. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.13 Криптографічні протоколи. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.14 Криптографічні протоколи направленого шифрування. Приклади розв’язку задач та задачі для самостійного розв’язання
- •Побудуйте однораундовий протокол автентифікації, використовуючи rsa криптографічне перетворення, оцініть стійкість протоколу, якщо довжина модуля
- •1) Факторизуємо модуль n і визначаємо прості числа p та q;
- •2.15 Криптографічні протоколи виробки та установки ключів. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.16 Криптографічні протоколи розподілу таємниці. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.17 Функції гешування та їх властивості. Приклади розв’язку задач та задачі для самостійного розв’язання
- •2.17.1 Приклади розв’язку задач
2.11 Стійкість асиметричних криптосистем, що базуються на криптоперетвореннях в групі точок еліптичних кривих. Приклади розв’язку задач та задачі для самостійного розв’язання
2.11.1 Основні теоретичні відомості
В пошуках криптографічних алгоритмів з відкритим розповсюдженням ключів з експоненціальною складністю криптоаналізу спеціалісти зупинились на криптографічних перетвореннях, що виконуються в групі точок ЕК. Відповідно до прогнозів ці перетворення ще довго забезпечуватимуть необхідний рівень стійкості. Розглянемо основні задачі криптоаналізу для систем, в яких перетворення здійснюються в групі точок ЕК, методи їх розв’язання та дамо оцінку стійкості для відомих нам методів криптоаналізу.
Під час аналізу стійкості необхідно розглядати дві проблеми стійкості розв’язання задачі дискретного логарифму та задачі Діффі-Хеллмана.
Проблема дискретного логарифму формується в наступному вигляді. Нехай задано точку G на еліптичній кривій E(F(q)), де q=p (p просте число) або q=pm (p просте число, m натуральне, mN). Відомо також значення відкритого ключа Q, причому
 . (2.99)
. (2.99)
Необхідно знайти конфіденційний (особистий) ключ d.
Проблема
Діффі-Хеллмана формується в наступному
вигляді. Нехай дано ЕК E(F(q)),
відомо значення точки
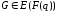 ,
а також відкритий ключ
,
а також відкритий ключ .
Необхідно знайти загальний секрет
.
Необхідно знайти загальний секрет
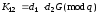 ,
(2.100)
,
(2.100)
де
 та
та
особисті ключі відповідно першого та
другого користувачів.
особисті ключі відповідно першого та
другого користувачів.
На
сьогодні для аналізу стійкості та
проведення криптоаналізу знайшли
розповсюдження декілька методів Поларда
 та оптимальний
та оптимальний .
Розглянемо
.
Розглянемо метод Поларда на прикладі ЕК над простим
полем Галуа
метод Поларда на прикладі ЕК над простим
полем Галуа ,
тобто
,
тобто
 .
(2.101)
.
(2.101)
Для
всіх точок
 задано операції додавання та подвоєння.
Наприклад, якщо
задано операції додавання та подвоєння.
Наприклад, якщо ,
а
,
а ,
то
,
то
 ,
,
де
 (2.102)
(2.102)
Для
ЕК над полем
 виду
виду
 ,
(2.103)
,
(2.103)
причому
 ,
сума двох точок
,
сума двох точок та
та
 ,
,
де
 (2.104)
(2.104)
 примітивний
поліном m-го
ступеня;
примітивний
поліном m-го
ступеня;
 (2.105)
(2.105)
Для
розв’язання задачі пошуку конфіденційного
ключа
 в порівнянні (2.99) розглянемо
в порівнянні (2.99) розглянемо -метод
Поларда над простим полем
-метод
Поларда над простим полем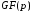 .
Нехай
.
Нехай
базова точка,
базова точка,

відкритий ключ, шукатимемо пари цілих
відкритий ключ, шукатимемо пари цілих
 та
та ,
таких що
,
таких що
 .
(2.106)
.
(2.106)
Позначимо в загальному вигляді
 .
(2.107)
.
(2.107)
Суть
 -методу
Поларда розв’язання порівняння (2.99)
заключається в наступному. Знайдемо
деяку функцію
-методу
Поларда розв’язання порівняння (2.99)
заключається в наступному. Знайдемо
деяку функцію ,
вибравши
,
вибравши ,
де
,
де
порядок точки
порядок точки
 на ЕК
на ЕК
 .
(2.108)
.
(2.108)
Далі
знайдемо
 послідовність:
послідовність:

для
пар
 ,
таких що:
,
таких що:
 .
(2.109)
.
(2.109)
Рекомендується
в простих випадках (при відносно невеликих
 )
послі-довність
)
послі-довність розраховувати у вигляді:
розраховувати у вигляді:
 (2.110)
(2.110)
При
цьому
 ,
, та
та складають частини області
складають частини області .
Якщо область
.
Якщо область рівномірно ділиться, то (2.11.12) має вигляд:
рівномірно ділиться, то (2.11.12) має вигляд:
 (2.111)
(2.111)
При
побудові множини
 пошук буде успішним, якщо ми знайдемо
пошук буде успішним, якщо ми знайдемо
 ,
,
що еквівалентно знаходженню
 .
(2.112)
.
(2.112)
Зробивши прості перетворення, маємо:
 (2.113)
(2.113)
і далі
 . (2.114)
. (2.114)
З (2.99) та (2.114) випливає, що
 , (2.115)
, (2.115)
 .
.
Більш
ефективним є розрахунок
 з розбиванням інтервалу
з розбиванням інтервалу на
на інтервалів. Для реальних значень
інтервалів. Для реальних значень рекомендується
рекомендується .
В цьому випадку замість (2.110) маємо
.
В цьому випадку замість (2.110) маємо
 (2.116)
(2.116)
причому
 та
та є випадкові цілі із інтервалу
є випадкові цілі із інтервалу .
.
У випадку (2.116) рішення знаходиться як і раніше у вигляді (2.111), а потім (2.115). З урахуванням позначень в (2.116)
 . (2.117)
. (2.117)
Успішне розв’язання задачі дискретного логарифму в групі точок ЕК вимагає
 (2.118)
(2.118)
операцій на ЕК.
Із
(2.117) та (2.118) випливає, що задачу пошуку
пар
 та
та може бути розпаралелено на
може бути розпаралелено на процесів, тоді
процесів, тоді
 .
(2.119)
.
(2.119)
Розроблено методику та алгоритми, які дозволяють розв’язати задачу (2.99) зі складністю
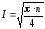 ,
(2.120)
,
(2.120)
а
при розпаралелюванні на
 процесорах складність визначається,
як
процесорах складність визначається,
як
 .
(2.121)
.
(2.121)
При
розв’язанні задачі важливо правильно
(вірніше успішно) вибрати
 .
Значення
.
Значення рекомендується вибирати у вигляді
рекомендується вибирати у вигляді
 .
.
 також
можна вибирати як
також
можна вибирати як
 , (2.122)
, (2.122)
де
 .
.
2.11.2 Приклади розв’язку задач
Задача 1.
Нехай
точка
 належить ЕК
належить ЕК
 ,
,
причому
 і
і ,
тобто
,
тобто
 .
.
Відкритий
ключ
 .
Порядок точки
.
Порядок точки ,
порядок ЕК
,
порядок ЕК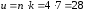 ,
де
,
де
кофактор. Необхідно знайти відкритий
ключ
кофактор. Необхідно знайти відкритий
ключ
 із порівняння
із порівняння
 .
.
В нашому випадку
 .
.
Розв’язання задачі.
Використовуючи співвідношення (2.110), отримаємо
 (2.123)
(2.123)
Результати розв’язку задачі наведено в таблиці 2.20.
Таблиця 2.20 – Результати розв’язку задачі 1
|
|
|
|
|
|
|
1 |
0 |
|
|
|
2 |
0 |
|
|
|
4 |
0 |
|
|
|
4 |
1 |
|
 ,
,
 ,
,
 .
.
Виберемо
як
 ,
тоді
,
тоді належить
належить ,
тому
,
тому
 .
.
Згідно з (2.102)


Розв’язуємо це рівняння, використовуючи алгоритм Евкліда

Отже
 .
Таким чином
.
Таким чином .
.


В результаті маємо, що

Таким
чином
 .
.
Другий крок
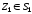 .Знаходимо
.Знаходимо
![]() .
.

Мультиплікативно
зворотний елемент числу 2 в полі
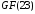 знаходимо із
рівняння
знаходимо із
рівняння

дійсно


 ;
;
 .
.
Таким чином
 ;
;
 ;
;
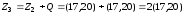 .
.
Знаходимо

 ;
;

 .
.
Таким чином в таблиці ми знайшли, що
 ;
;


Знаходимо
 .
.
Перевіряємо
 .
.

 .
.
Таким чином

 .
.
Задача 2.
Визначте
складність та вартість криптоаналізу
методом повного розкриття для
криптоперетворень в групі точок ЕК над
полем
 ,
якщо порядок базової точки
,
якщо порядок базової точки ,
потужність криптоаналітичної системи
,
потужність криптоаналітичної системи додавань на ЕК/с., а вартість одного
міпсороку складає
додавань на ЕК/с., а вартість одного
міпсороку складає грн.
грн.
Розв’язок задачі.
Знайдемо
складність криптоаналізу, вважаючи, що
він здійснюється методом повного
розкриття з використанням оптимального
методу
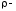 Поларда.
В цьому випадку складність криптоаналізу
визначається з використанням формули
(2.120)
Поларда.
В цьому випадку складність криптоаналізу
визначається з використанням формули
(2.120)
 .
.
В
таблиці 2.21 наведено значення складності
криптоаналізу методом повного розкриття,
тобто з визначенням таємного ключа
 .
Одиницею виміру складності є число
операцій додавання в групі точок ЕК.
.
Одиницею виміру складності є число
операцій додавання в групі точок ЕК.
Таблиця 2.21 Складність криптоаналізу
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Знаючи загальну складність, вартість криптоаналізу визначаємо таким чином: безпечний час виконання криптоаналізу (в роках)
 ,
,
де
 с./рік.
с./рік.
Для
досягнення потужності криптоаналітичної
системи
 оп/с
необхідно затратити
оп/с
необхідно затратити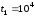 років
років або паралельно використати
або паралельно використати комп’ютерів з потужністю
комп’ютерів з потужністю оп.
додавання на ЕК/с. Тому вартість
криптоаналізу можна визначити як
оп.
додавання на ЕК/с. Тому вартість
криптоаналізу можна визначити як
 .
.
В таблиці 2.22 наведено значення безпечного часу та вартості криптоаналізу.
Таблиця 2.22 Безпечний час та вартість криптоаналізу
|
|
|
|
|
|
|
|
|
|
|
|
Задача 3.
Порівняйте криптоперетворення в кільцях, полях та групі точок ЕК за критерієм складності виконання. Визначте вартість криптоаналізу методом пов-ного розкриття, при якому криптоаналітик знаходить секретний (особистий) ключ абонента, якщо довжини модулів криптоперетворень в кільці, полі та групі точок ЕК відповідно дорівнюють
 бітів.
бітів.
Потужність
криптоаналітичної системи в кільці та
полі складає
 ,
а в групі точок ЕК
,
а в групі точок ЕК .
Вартість одного міпсороку складає для
криптоперетворень в кільці та полі 30
грн., а в групі точок ЕК
600 грн.
.
Вартість одного міпсороку складає для
криптоперетворень в кільці та полі 30
грн., а в групі точок ЕК
600 грн.
Розв’яжемо
задачу при
 .
.
При
 маємо
маємо .
Спочатку визначаємо складність
криптоаналізу для перетворень в кільці.
Очевидно найменш складним буде
криптоаналіз, що застосовується на
факторизації модуля перетворення
.
Спочатку визначаємо складність
криптоаналізу для перетворень в кільці.
Очевидно найменш складним буде
криптоаналіз, що застосовується на
факторизації модуля перетворення з використанням загального решета
числового поля. Вона визначається як
з використанням загального решета
числового поля. Вона визначається як
 .
(2.124)
.
(2.124)
При
криптоаналізі криптографічних перетворень
в полі Галуа
 найбільш складною є задача розв’язку
дискретного логарифмічного рівняння
найбільш складною є задача розв’язку
дискретного логарифмічного рівняння
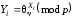 .
(2.125)
.
(2.125)
Складність
розв’язку (2.125) також може бути оцінена
з використанням (2.11.26), при цьому, якщо
розв’язок (2.125) базується на використанні
загального решета числового поля, то
 ,
при факторизації
,
при факторизації .
.
Складність
криптоаналізу в групі точок ЕК при
використанні оптимального методу
 Поларда
можна оцінити як
Поларда
можна оцінити як
 ,
(2.126)
,
(2.126)
де

порядок базової точки
порядок базової точки
 в групі точок ЕК. Таким чином для оцінки
складності криптоаналізу використовуємо
формули в кільці
в групі точок ЕК. Таким чином для оцінки
складності криптоаналізу використовуємо
формули в кільці
 .
.
В полі:
 .
.
В групі точок ЕК
 .
.
Для кільця маємо:


 .
.
Для поля маємо:
 .
.
Для групи точок ЕК
 .
.
Наступні
задачі 4
8 є додаткові, вони призначені для
практичного засвоєння перетворень в
розширених полях Галуа
 .
.
Задача 4.
Знайдіть
елементи поля
 ,
якщо неприводимий поліном
,
якщо неприводимий поліном .
.
Розв’язок.
Враховуючи,
що поле
 містить 16 елементів та використовуючи
поліноміальне перетворення, маємо:
містить 16 елементів та використовуючи
поліноміальне перетворення, маємо:

Задача 5.
Знайдіть
суму та добуток елементів поля
 ,
якщо
,
якщо .
.
Розв’язок.
Сума
за модулем 2:
 .
.
Добуток
має вигляд:
 .
.
Дійсно
 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 6.
Знайдіть
усі елементи поля
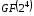 ,
використовуючи первисний елемент поля
,
використовуючи первисний елемент поля ,
, .
.
Розв’язок.

|
|
| ||||||
|
|
|

|
|
|
Задача 7.
Нехай
 супернесингулярна крива над полем
супернесингулярна крива над полем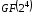 .
Примітивний поліном
.
Примітивний поліном .
Знайдіть точки, які задовольняють цьому
рівнянню.
.
Знайдіть точки, які задовольняють цьому
рівнянню.
Розв’язок.


Порівняння
має вигляд:
 .
.
Розв’язком є точки:












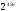










 (років)
(років)
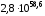
 (грн.)
(грн.)


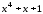



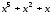














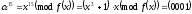 .
Дійсно
.
Дійсно


