2.9 Симетричні потокові шифри. Приклади розв’язку задач та задачі для самостійного розв’язання

2.9.1 Приклади розв’язку задач

Задача 1.

Визначити період повторення двійкової послідовності, що формується за допомогою двох лінійних рекурентних регістрів ЛРР1 та ЛРР2, якщо ЛРР1 та ЛРР2 реалізовані з використанням примітивних поліномів 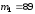тапорядків відповідно.

Розв’язок задачі.

Оскільки числа 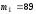та 127 є прості числа Ейлера і періоди повтореньта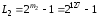є також прості числа, то період повторенняL послідовності, що формується згідно з ЛРР1 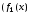примітивний поліном) та ЛРР2примітивний поліном)

.

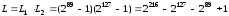Якщо 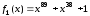і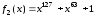, то послідовністьL може бути сформована з використанням схеми, що наведена на рис. 2.22.

Рисунок 2.22  Схема формування двійкової послідовності з періодом L

Задача 2.

Визначте закон формування гами скремблювання, якщо відомі відрізки послідовності

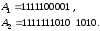
Покладемо спочатку, що ці послідовності сформовані лінійним рекурентним регістром m-го порядку з поліномом (для А₁) і, що перехоплено 2m символів. Значить для А₁ m=5.

Еквівалентна схема такого регістра наведена на рис. 2.23

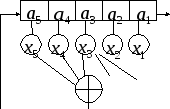
Рисунок 2.23  Еквівалентна схема ЛРР з невідомим зворотним зв’язком

Присвоюючи вектору 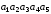послідовно значення 11111, 11110, 11100, 11000, 10000, отримаємо систему лінійних рівнянь

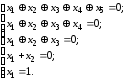
Цю систему можна розв’язати будь-яким методом, враховуючи тільки, що і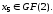

Із системи зразу видно, що 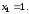Далі, підставивши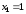в наступне рівняння, маємо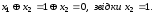

Підставивши в третє рівняння, маємо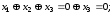значить

Далі, підставивши в четверте рівняння, маємо

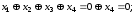значить

Підставивши в останнє рівняння, маємо

Таким чином, тільки 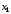і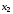не є нульові, тому

Для вектора А₂ маємо систему рівнянь

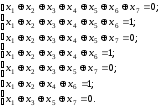
Розв’язок задачі.

Складемо за модулем 2 перше та друге рівняння системи

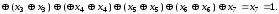
Далі складемо перше та третє рівняння

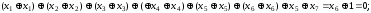
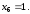
Складемо перше та четверте рівняння

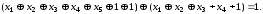
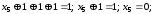
Складемо перше та шосте рівняння

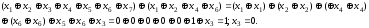Складемо п’яте та сьоме рівняння

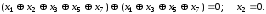
Складемо шосте та сьоме рівняння

.

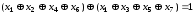
Підставивши в останнє рівняння значення х_3, х₅ та х₇, маємо

.

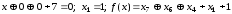Перевірка.

Згенеруємо послідовність згідно з .

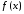На рис. 2.24 наведено схему ЛРР

Рисунок 2.24  Схема ЛРР

Сформуємо послідовність, підставивши в ЛРР початкове значення його стану „1111111”.

Таким чином, вихідною є послідовність „11111110101010” і вона співпадає з А₂, тобто розв’язок зроблено правильно.

„Увага” – колізія. Перевірте чи можна сформувати послідовність А₂ з використанням ЛРР, у якого зворотний зв’язок реалізовано з використанням полінома 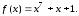Якщо можна, то зробіть відповідні пояснення

Задача 3.

Розробіть спрощену структурну схему та проведіть дослідження стійкості потокового шифру А5, що застосовується в системі зв’язку GSM.

Шифр А5 [10]– це потоковий шифр, що використовується в системі мобільного зв’язку GSM. Це європейський стандарт для мобільних цифрових сотових телефонів. Алгоритм А5 використовується для шифрування каналу “телефон/базова станція”. Відомо, що в середині восьмидесятих років різні таємні служби НАТО розв’язували задачу, чи має шифрування GSM бути сильним чи слабким. Німцям необхідна була сильна криптографія, так як вони були на кордоні з Варшавським договором. Але перемогла друга точка зору, був прийнятий відносно слабкий шифр А5, який розроблено Францією. Британська телефонна компанія передала всю документацію Брендфордському університету, забувши підписати з ним угоду про її конфіденційність. В результаті інформація про А5 була опублікована в Інтернет. Програмна реалізація А5 наведена в [10].

Структурна схема шифроутворюючого пристрою наведена на рис. 2.25. В склад пристрою входить три ЛРР з довжинами 19,22 та 23 бітів відповідно. Всі многочлени зворотного зв’язку є прорідженими. Виходом є результат операції XOR над трьома ЛРР. В А5 використовується також управління тактуванням. Кожний регістр тактується в залежності від свого середнього біта, потім над регістром виконується операція XOR зі зворотною пороговою функцією середніх бітів усіх трьох регістрів, звичайно на кожному етапі тактуються два ЛРР.

Знайдено тривіальне розкриття А5, що вимагає 2⁴⁰ шифрувань: якщо припустити відомими стани перших двох регістрів, то можна за гамою-шифруючою спробувати визначити стан третього ЛРР.

Рисунок 2.25 – Структурна схема алгоритму А5

В цілому, ідеї, що закладені в А5 є потужними. Алгоритм є ефективним, він задовольняє статистичним тестам. Єдиною його слабкістю є замалі довжини регістрів.

Оцінимо значення основних показників шифру А5 – безпечний час t_б, ентропію джерела ключів та відстань єдності

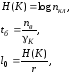
де n_кл=2⁶⁴ – число ключів, n_в=2⁴⁰ – число варіантів під час криптоаналізу, =10¹⁰  – потужність криптоаналітичної системи, k=3,1510⁷ с/рік, r – збитковість вихідного алфавіту.

В результаті маємо

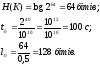
Задача 4.

Побудуйте генератор Геффе та дослідіть його властивості [10].

Структурна схема генератора Геффе наведена на рис. 2.26.

Рисунок 2.26 – Структурна схема генератора Геффе

В генераторі Геффе використовується комбінація із трьох ЛРР. Два ЛРР (ЛРР2-ЛРР3) є джерелами гам початкових, а ЛРР1 управляє виходом мультиплексера. Якщо та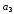є виходами відповідних ЛРР, то вихід генератора можна задати у вигляді

.

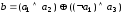Якщо довжини ЛРР є відповідно 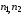та, то лінійна складність генератора може бути оцінена як [10]

.

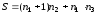Період генератора дорівнює найменшому спільному кратному періодів трьох ЛРР. Якщо степені трьох примітивних поліномів зворотного зв’язку взаємно прості, то період цього генератора дорівнюватиме добутку періодів трьох ЛРР.

Основним недоліком генератора Геффе є незахищеність від кореляційної атаки [10].

Задача 5.

Побудуйте генератор Дженнінгса та дослідіть його властивості.

В генераторі Дженнінгса мультиплексор використовується для об’єднання бітів двох ЛРР [10]. Мультиплексор, що управляється ЛРР1, вибирає як черговий вихідний 1 біт ЛРР2. Крім того, використовується функція, що відображає вихід ЛРР2 на вхід мультиплексора. Структурна схема генератора Дженнінгса наведена на рис. 2.27.

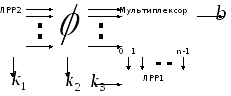
Рисунок 2.27 – Структурна схема генератора Дженнінгса

Ключем в генераторі є початковий стан двох ЛРР- ЛРР1 та ЛРР2, а також функція відображенн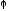я . Дослідження показали, що на генератор можна реалізувати ефективні атаки типу “зустріч посередині” та “кореляційне розкриття”.