
Дифф_Исчисление_11
.pdf
y′′ |
- |
|
+ |
|
- |
|
у |
Ç |
0 |
È |
2 |
Ç |
х |
|
|
|
Рис. 12.8 |
|
|
|
у |
|
|
|
График данной функции представлен |
||
|
|
|
|
на рис. 12.9 |
|
|
ln 2

0 |
1 |
2 |
х |
Рис. 12.9
12.4 Асимптоты графика функции
Определение. Пусть для функции y = f (x) существует такая прямая, что расстояние от точки M (x, f (x)) графика функции до этой прямой стремится к ну-
лю при бесконечном удалении точки M от начала координат. Тогда такая прямая называется асимптотой графика функции.
Из определения видно, что если график функции имеет асимптоту, то «вда- ли» от начала координат он похож на прямую линию.
y |
|
В случае вертикальной асимптоты неогра- |
||||||
|
ниченное удаление точки графика от начала ко- |
|||||||
|
|
|
|
|||||
|
y = f (x) |
|
x = x0 |
ординат равносильно тому, что |
|
f (x) |
|
→ ∞ при |
|
|
|||||||
|
|
|
|
x → x0 , а стремление к нулю расстояния между |
||||
|
|
|
|
|||||
|
|
|
x |
графиком и асимптотой равносильно тому, что |
||||
|
|
|
x → x0 . Отсюда следует |
|||||
|
|
|
|
|||||
|
|
|
|
61 |
|
|
|
|

ТЕОРЕМА. Прямая x = x0 является вертикальной асимптотой графика
функции y = f (x) тогда и только тогда, когда хотя бы одно из предельных значе-
ний lim f (x) или |
lim f (x) равно + ∞ или –∞. |
x→x0 −0 |
x→x0 +0 |
Замечание. Непрерывные функции вертикальных асимптот не имеют. Можно заметить, что вертикальные асимптоты тесно связаны с точками раз-
рыва второго рода.
1
Пример 12.8. Найти вертикальные асимптоты графика функции f (x) = 3x−2 .
|
|
|
1 |
|
|
|
|
1 |
→ −∞ = 3−∞ |
|
||
Находим lim |
3 |
x−2 |
= |
x − 2 → −0, |
= 0 , |
|||||||
x − 2 |
||||||||||||
|
x→2−0 |
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
1 |
→ +∞ = 3+∞ = +∞ . Здесь прямая x = 2 (y ³ 0) – |
|||||
lim 3 |
x−2 |
= |
x − 2 → +0, |
|||||||||
x − 2 |
||||||||||||
x→2+0 |
|
|
|
|
|
|
|
|
||||
правая вертикальная асимптота. Заметим, что x = 2 – точка разрыва второго рода.
Замечание. Если |
lim f (x) ¹ ¥ и f (x0 ) не существует, то x0 – точка разры- |
||||||
|
x→x0 |
|
|
|
|
||
ва функции. |
|
|
|
|
|
|
|
Пример 12.9. f (x) = |
sin x |
, |
f (0) не существует. Имеем |
lim |
sin x |
=1. Верти- |
|
|
|
||||||
|
|
x |
|
x→0 |
x |
||
кальных асимптот график функции не имеет. |
|
|
|
||||
Пример 12.10. |
Функция |
f (x) = ln x не имеет |
разрывов, однако |
||||
lim ln x = -¥. Поэтому x = 0 – вертикальная асимптота. |
|
|
|
||||
x→+0 |
|
|
|
|
|
|
|
Перейдем к вопросу о нахождении наклонных асимптот.
|
|
|
|
|
|
|
ТЕОРЕМА. |
Для |
существования наклонной асимптоты |
y = kx + b |
графика |
функции y = f (x) при |
x → +∞ ( x → −∞) необходимо и достаточно, чтобы суще- |
||||
ствовали конечные пределы:
62

lim |
f (x) |
= k Ù lim ( f (x) - kx) = b |
|
(12.4.1) |
||
|
x |
|
||||
x→+∞ |
|
|
x→+∞ |
|
|
|
æ |
|
f (x) |
|
ö |
|
|
ç lim |
|
|
|
= k Ù lim ( f (x) - kx) = b÷ . |
(12.4.2) |
|
|
|
|
||||
è x→−∞ x |
|
x→−∞ |
ø |
|
||
|
|
|
При этом при |
x → +∞ |
и при |
|||||||
у |
|
|
x → −∞ |
указанные |
пределы |
могут |
||||||
|
|
|
быть различными (правая наклонная |
|||||||||
|
L |
|
асимптота |
и, |
|
соответственно, |
левая |
|||||
|
К |
|
наклонная асимптота). |
|
|
|
||||||
|
M (x, f (x)) |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
Доказательство. |
|
|
|
||||||||
|
α |
х |
|
|
|
|||||||
|
|
Пусть |
y = kx + b – |
наклонная |
||||||||
|
|
|
асимптота графика функции. Расстоя- |
|||||||||
|
Рис. 12.10 |
|
ние от точки графика функции до |
|||||||||
|
|
|
||||||||||
|
|
|
асимптоты изображается |
на |
рисунке |
|||||||
(Рис. 12.10) отрезком КМ. Заметим, что ÐKML = a, |
LM = |
|
KM |
|
. Так как коорди- |
|||||||
|
cosa |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
наты точки |
M есть (x, |
f (x)), то координаты точки L есть (x, kx + b). Поэтому |
||||||||||
LM = kx + b − f (x). По |
определению |
y = kx + b |
– |
|
наклонная |
асимптота |
||||||
KM → 0 LM → 0 lim ( f (x)− (kx + b)) = 0 b = lim ( f (x)− kx). |
|
Тогда |
||||||||||
|
|
x→+∞ |
|
|
x→+∞ |
|
|
|
|
|||
существует |
бесконечно |
малая функция β(x) |
при |
|
x → +∞ |
такая, |
что |
|||||
f (x)− kx = b + β(x). Разделим обе части последнего равенства на x и в полученном
равенстве |
|
|
|
перейдем |
|
к |
|
|
пределу |
при |
x → +∞ : |
||||||||||||
|
f (x) |
- k = |
b |
|
β(x) |
|
æ f (x) |
ö |
|
æ b |
|
b(x)ö |
|
|
k = lim |
f (x) |
|
||||||
|
|
|
|
+ |
|
|
, |
lim ç |
|
|
- k ÷ |
= |
lim ç |
|
+ |
|
÷ |
= 0. |
Отсюда |
|
. |
||
|
x |
|
x |
|
x |
|
|
x→+∞è |
x |
ø |
|
x→+∞è x |
|
x |
ø |
|
|
x→+∞ |
x |
|
|||
Теорема доказана.
Замечание. В случае k = 0 асимптота является горизонтальной.
63

Замечание. Если хотя бы один из пределов (12.4.1) при x → +∞ ((12.4.2)
при x → −∞ ) не существует или является бесконечным, то график функции на- клонных асимптот не имеет.
|
|
Пример 12.11.Найти асимптоты графика функции y = 3 |
|
|
− |
2x |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
x2 e |
|
3 . |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
Область определения функции D(y) = R ; |
y(x)³ 0 при x R , |
|
|
y(0)= 0. |
||||||||||||||||||||||||||||||||||||||||
Вертикальных асимптот нет, т. |
|
к. функция непрерывна при всех |
x R . Найдем |
|||||||||||||||||||||||||||||||||||||||||||
наклонные асимптоты y = kx + b : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
k |
|
= |
lim |
|
y(x) |
= lim |
|
|
|
|
1 |
|
|
|
|
|
= 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
+ |
|
|
x |
|
|
|
|
|
× e2x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
x →+∞ |
|
|
x→+∞ 3 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
3 |
|
|
|
ö′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
æ |
¥ ö |
|
|
ç |
|
÷ |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||
b |
|
lim |
y(x) = |
lim |
|
|
|
|
|
|
|
|
|
|
|
lim |
è |
|
|
ø |
|
|
lim |
|
|
|
|
|
|
= 0 |
|
|||||||||||||||
= |
|
|
|
|
|
|
|
|
|
= |
ç |
|
÷ = |
(e2x 3 )¢ |
= |
|
|
|
|
|
|
|
|
; |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
+ |
|
x→+∞ |
|
|
|
|
x→+∞ e2x 3 |
|
|
è |
¥ ø |
|
x→+∞ |
|
x→+∞ 3 |
x |
×e2x 3 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
y(x) |
|
|
|
|
e− 2x 3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
e−2x 3 |
|
|
|
|
|
|
|
|
||||||||||||||
k− |
|
|
|
|
|
|
|
|
|
|
|
æ ¥ |
ö |
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
= |
lim |
|
|
|
= |
lim |
|
|
|
|
|
|
|
|
|
|
|
= ç |
÷ |
= -2 |
lim |
|
|
|
|
|
|
|
|
|
= -¥ . |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
x |
|
|
|
3 x |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
x→−∞ |
|
|
x→+∞ |
|
|
|
è ¥ |
ø |
|
x→+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
Следовательно, при |
|
x → +∞ |
имеем |
|
правую |
горизонтальную |
асимптоту |
|||||||||||||||||||||||||||||||||||||
y = 0; при x → −∞ наклонных и горизонтальных асимптот нет.
12.5Схема исследования функций и построения кривых
1.Найти область определения функции.
2.Отметить особенности функции (периодичность, четность и нечетность, со- хранение знака), найти точки пересечения графика функции с осями координат.
3.Если граничные точки области определения функции принадлежат ей, то найти значение функции в этих точках, в противном случае – выяснить поведение функции в окрестности этих точек, найти вертикальные асимптоты, если они су- ществуют.
64

4.Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты или убедиться в их отсутствии.
5.Найти интервалы монотонности функции и точки экстремума.
6.Указать интервалы сохранения направления выпуклости и точки перегиба графика функции.
По результатам исследования функции строится ее график. Пример 12.12. Исследовать функции и начертить их графики:
1. |
y = |
(x −1)3 |
; |
|
|
2. y = 3 |
|
e− |
2x |
|
|
|
||||||||||
|
|
|
x2 |
3 |
; |
|
|
|
||||||||||||||
3(x + 1)2 |
|
|
|
|||||||||||||||||||
|
f (x) = 2x - 33 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. |
(x -1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1. |
y = |
(x −1)3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
3(x + 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А) |
Область определения |
функции |
|
|
D(y)= (− ∞;−1)U (−1;+∞). Функция |
|||||||||||||||||
обращается в ноль при |
x =1, при |
x = 0 |
y = − |
|
1 |
|
, т. е. график функции пересекает |
|||||||||||||||
3 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
æ |
|
1 |
|
ö |
|
|
|
|
|
|
|
|
|
|
||
ось Ox в точке (1; 0), ось Oy в точке ç |
0;- |
|
|
÷. При |
x (− ∞; − 1)U (− 1;1) |
y < 0 , а |
||||||||||||||||
3 |
|
|||||||||||||||||||||
|
|
|
|
|
|
è |
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|||
при x (1;+ ∞) y > 0 (рис. 12.11). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
sgn y |
- |
|
- |
|
|
|
|
|
|
|
|
+ |
|
x |
|
|
||||
|
|
|
-1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
Рис. 12.11 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Б) |
Исследуем |
точку разрыва |
x = −1. |
Так |
как |
пределы функции |
при |
|||||||||||||||
x → −1− 0 |
(слева) |
и при |
x → −1+ 0 |
|
|
|
(справа) |
бесконечны, |
т. |
е. |
||||||||||||
65

lim |
(x -1)3 |
= -¥ , |
lim |
(x -1)3 |
= -¥, то прямая |
|
|
||||
x→−1−0 3(x +1)2 |
|
x→−1+0 3(x + 1)2 |
|
||
кальной асимптотой.
Найдем наклонные асимптоты y = kx + b :
k = lim |
y |
= lim |
|
(x -1)3 |
|
= |
1 |
, |
|
|
|
|
|
|
|
|
||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x→∞ |
x→∞ 3x (x +1)2 |
|
3 |
|
|
|
|
|
|
|
|
|||||||
b = lim (y - k x)= |
|
1 |
æ |
(x -1)3 |
ö |
|
|
|
|
1 |
æ |
- 5x2 + 2x |
||||||
lim |
|
ç |
|
|
|
|
- x÷ |
= |
lim |
|
ç |
|
||||||
|
|
|
2 |
|
2 |
|||||||||||||
x→∞ |
|
|
|
x→∞ 3 |
ç |
|
|
÷ |
|
|
x→∞ 3 |
ç |
||||||
|
|
|
è |
(x + 1) |
ø |
|
|
è |
(x +1) |
|||||||||
Итак, наклонная асимптота y = |
1 |
x - |
5 |
. |
|
|
||||||||||||
3 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||
x = −1 является верти-
-1 |
ö |
= - |
5 |
. |
|
÷ |
3 |
||
|
÷ |
|
|
|
|
ø |
|
|
|
В) Промежутки монотонности и экстремумы данной функции определе-
ны в п. 12.2 (пример 12.3). |
|
|
|
|
Г) |
Определим промежутки выпуклости и |
точки |
перегиба |
графика |
|
|
y¢¢(x)= |
8 (x −1) |
|
функции. |
Находим вторую производную функции: |
(x + 1)4 . |
Точки из |
|
области определения первой производной, в которых вторая производная обращается в нуль или не определена, являются точками возможного перегиба графика функции. В нашем случае это точка x =1. Так как y′′ > 0 при x (1; + ∞),
то на этом интервале график функции является выпуклым вниз. Аналогично при
x (− ∞; −1) и при x (−1;1) |
y′′ < 0 , т. е. на соответствующих интервалах график |
|||
функции является выпуклым |
вверх. |
Следовательно, |
точка (1; 0) – это точка |
|
перегиба графика функции (рис. 12.12). |
|
|
|
|
y′′ |
- |
- |
|
+ |
у |
Ç -1 |
Ç |
1 |
È х |
Рис. 12.12
66
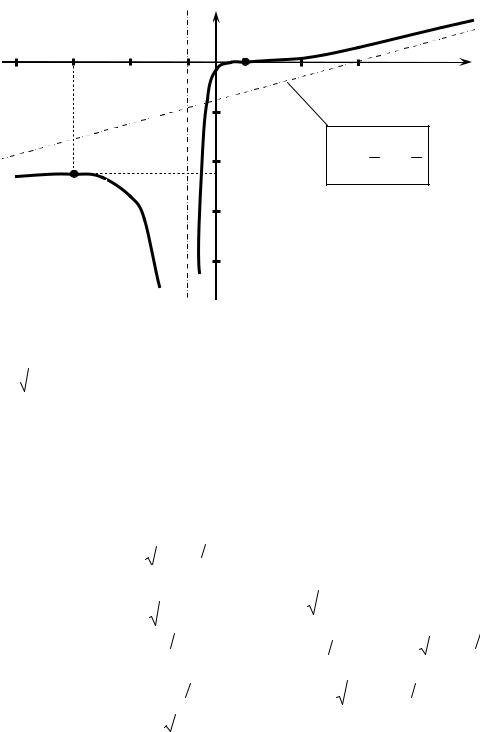
График данной функции, построенной по результатам исследования, пред- ставлен на рис. 12.13.
|
у |
|
|
(1; 0) |
|
− 1 |
5 |
х |
|
− 2 |
|
y = 13 x − 53
(−5;−4,5)
Рис. 12.13
|
|
|
|
|
|
|
− |
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
y = 3 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2. |
3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
А) |
|
Область определения функции D(y) = R ; |
|
y(x)³ 0 при x R , y(0)= 0. |
||||||||||||||||||||||||||||||||||||||||
Б) |
|
Вертикальных асимптот нет, т. |
к. |
функция непрерывна |
при всех |
|||||||||||||||||||||||||||||||||||||||
x R . Найдем наклонные асимптоты y = kx + b : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
k |
|
= |
lim |
|
y(x) |
|
= lim |
|
|
|
|
|
|
|
1 |
|
|
|
|
= 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
× e2x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
+ |
|
x →+∞ |
|
x |
|
|
|
|
x→+∞ 3 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ3 |
|
|
|
|
ö′ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
æ ¥ |
ö |
|
ç |
|
|
|
÷ |
|
|
|
|
|
1 |
|
||||||||||
b+ |
|
|
|
|
|
y(x)= |
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
ø |
|
|
|
|
|
|
||||||||||||||
= |
lim |
|
lim |
|
|
|
|
|
|
|
|
|
|
= |
ç |
¥ |
÷ = |
lim |
|
|
|
|
|
|
|
|
= |
lim |
|
|
|
|
= 0 ; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
x→+∞ |
|
|
|
|
|
|
x→+∞ e2x 3 |
|
è |
ø |
x→+∞ (e2x 3 )¢ |
|
x→+∞ 3 x × e2x 3 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
y(x) |
|
|
|
|
|
e− 2x 3 |
|
|
|
|
|
|
|
3 |
|
|
e−2x 3 |
|
|
|
|||||||||||||||||
k− |
|
|
|
|
|
|
|
|
|
|
|
æ |
¥ ö |
|
|
|
|
|
x2 |
|
|
|
||||||||||||||||||||||
= |
lim |
|
|
|
|
|
= |
lim |
|
|
|
|
|
|
|
|
|
|
= ç |
÷ |
= -2 |
lim |
|
|
|
|
|
|
|
|
|
= -¥. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
x |
|
|
|
3 x |
|
|
|
|
|
|
|
1 |
|
|
|
||||||||||||||||||||||||||||
|
|
|
x→−∞ |
|
|
x→+∞ |
|
|
|
|
|
è |
¥ ø |
|
x→+∞ |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Следовательно, при x → +∞ имеем правую горизонтальную асимптоту y = 0; при x → −∞ наклонных и горизонтальных асимптот нет.
67
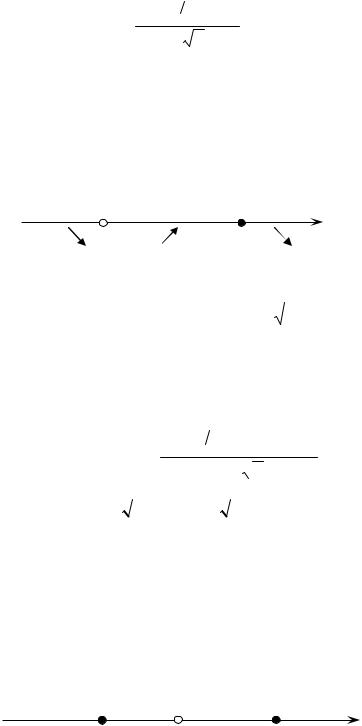
В) Определим промежутки монотонности и экстремумы данной функции.
Первая производная функции: y¢ = 2e− 2x 3 (1 - x). Находим критические точки: 3 3 x
y′ = 0 при x =1 и y′ не существует при x = 0. При x Î(- ¥; 0) и при x Î(1; + ¥)
y′ < 0 , при x Î(0;1) y′ > 0 . На каждом из промежутков (- ¥; 0], |
[1; + ¥) функция |
|||||||
убывает, на промежутке x Î[0;1] функция возрастает (рис. 12.14); |
||||||||
|
y′ |
- |
+ |
- |
|
|
|
|
|
y |
0 |
1 |
|
|
|
х |
|
|
|
Рис. 12.14 |
|
|
|
|
|
|
|
|
|
æ |
3 |
|
|
ö |
0,51); в точке |
|
|
|
e |
−2 |
||||
локальный минимум (0; 0); локальный максимум ç1; |
|
÷ » (1; |
||||||
|
|
|
è |
|
|
ø |
|
|
(0; 0) – вертикальная полукасательная x = 0, y(x)³ 0 . |
|
|
|
|
||||
Г) |
Определим |
промежутки |
выпуклости |
и |
|
точки |
перегиба графика |
|
функции. Вторая производная y¢¢(x)= 2e−2x 3 (2x2 - 4x -1). Найдем корни уравне- 9 x 3 x
x
ния 2x 2 - 4x - 1 = 0 |
: x |
=1 - |
|
6 |
|
, |
x |
2 |
=1+ |
|
6 |
(x » -0,22; x |
2 |
» 2,22). Так как |
||||
|
|
|
|
|
||||||||||||||
|
1 |
|
2 |
|
|
|
|
2 |
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y′′ > 0 при x Î (- ¥; x ) |
и при x Î(x |
; + ¥), то на этих интервалах график функции |
||||||||||||||||
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
является выпуклым вниз. Аналогично при x (x ; 0)U (0; x |
2 |
) |
y′′ < 0, т. е. на соот- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
ветствующих интервалах график функции выпуклый вверх, рис. 12.15. |
||||||||||||||||||
y′′ |
+ |
|
– |
|
|
|
|
|
– |
|
+ |
|
|
|
|
|
||
у |
È х1 |
Ç 0 |
Ç х2 |
È х |
|
|
||||||||||||
|
|
|
|
|
|
Рис. 12.15 |
|
|
|
|
|
|
|
|
|
|||
Точки перегиба графика |
функции |
|
(x1; y1 ), |
(x2 ; y2 ). |
|
Здесь |
y1 = y(x1 )» 0,43, |
|||||||||||
|
|
|
|
|
|
|
|
|
68 |
|
|
|
|
|
|
|
|
|
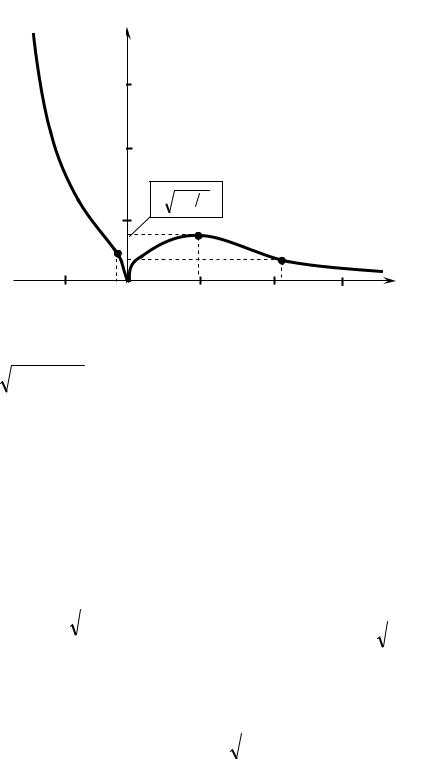
y2 = y(x2 )≈ 0,39. График функции представлен на рис. 12.16. |
|
|
|||||
|
|
у |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 e-2 3 |
|
|
|
|
|
|
−1 |
x1 |
1 |
2 х2 |
3 |
х |
|
|
|
Рис. 12.16 |
|
|
|
|
|
3. y = 3 (x + 3) x2 . |
|
|
|
|
|
||
А) |
Область |
определения |
x R ; |
y = 0 при |
x = 0 |
и при |
x = −3. При |
x (− ∞; − 3) y < 0 , а при x (− 3; 0)U (0;+∞) y > 0 . Точки (− 3; 0) и (0; 0) являют- |
|||||||
ся точками пересечения графика функции с осями координат. |
|
||||||
Б) |
Вертикальных асимптот нет, так как функция определена и непрерыв- |
||||||
на на множестве действительных чисел. |
Для наклонной асимптоты y = k x + b |
||||||
найдем коэффициенты: |
|
|
|
|
|
||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||
|
y |
|
|
(x + 3)x2 |
b = lim (y − k x)= lim (3 |
|
|
|||||||
k = lim |
= |
lim |
|
=1; |
(x + 3)x2 |
− x) =1, |
||||||||
|
|
|
|
|||||||||||
x→±∞ x |
x→±∞ |
|
x |
x→±∞ |
|
x→±∞ |
|
|
||||||
т. е. y = x +1 – наклонная асимптота. |
|
|
|
|
|
|||||||||
В) |
Найдем производную y′(x)= |
|
x + 2 |
|
; y′(x)= 0 при x = −2 и y′(x) |
|||||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
3 |
(x + 3)2 x |
|
|
|
|
|
не существует при x = −3 и при x = 0.
69

y′ |
+ |
+ |
|
- |
+ |
у |
|
− 3 |
− 2 |
0 |
х |
|
|
Рис. 12.17 |
|
|
|
При x (− 2; 0) y¢ < 0 ; при |
x (− ∞; − 3), |
x (− 3; − 2), |
x (0;+∞) y′ > 0 . На про- |
||
межутке [− 2; 0] функция убывает, на промежутках (− ∞; − 3], [− 3; − 2], [0;+∞) воз-
растает (рис. 12.17). В точке (-2; 3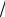 4 ) функция имеет локальный максимум, в точ-
4 ) функция имеет локальный максимум, в точ-
ке (0; 0) локальный минимум. Отметим, что y'(− 2)= 0 , т. е. график функции име-
ет в этой точке горизонтальную касательную. В точке (-3; 0) имеем вертикальную
|
|
(функция y = 3 |
|
|
|
|
|
|
|
|||||||
касательную |
x = −3 |
(x + 3) x2 |
в точке |
x = −3 |
непрерывна и |
|||||||||||
lim |
y'(x)= +∞). |
Поскольку |
y(x) |
|
непрерывна |
в |
нуле |
и |
||||||||
x→−3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
y′(x)= −∞, |
lim |
y′(x)= +∞ ; то полупрямая |
x = 0, |
y ³ 0 является и левой и |
|||||||||||
x→0− |
|
|
x→0 |
+ |
|
|
|
|
|
|
|
|
|
|
||
правой полукасательной к графику функции в точке (0; |
0). Следовательно, точка |
|||||||||||||||
(0; 0) - точка возврата кривой. |
|
|
|
|
|
|
|
|
|
|
||||||
|
Г) |
Определим промежутки выпуклости и точки перегиба графика функ- |
||||||||||||||
ции. Находим вторую производную |
y′′(x)= − |
|
|
|
2 |
. Знаки второй производ- |
||||||||||
|
|
|
|
|||||||||||||
3 x4(x + 3)5 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ной: |
y′′(x)< 0 |
при |
x (− 3; 0) и при |
x (0; + ∞), |
y′′(x) > |
0 |
при x (− ∞; − 3) |
(рис. |
||||||||
12.18). Точка перегиба графика функции (− 3; 0). На промежутке (-¥;-3) график функции выпуклый вниз; на промежутках (− 3; 0) и (0; +¥) – выпуклый вверх.
y′′ |
+ |
- |
- |
|
y |
È -3 |
Ç 0 |
Ç |
х |
|
|
|
|
|
Рис. 12.18
График функции представлен на рис. 12.19.
70
