
Дифф_Исчисление_11
.pdf
ТЕОРЕМА о необходимом и достаточном условии возрастания (убывания) функции
Пусть функция f (x) непрерывна на [a, b] и дифференцируема на (a, b). То-
гда:
1) для того чтобы функция f возрастала (убывала) на [a, b], необходимо и
достаточно, чтобы |
′ |
′ |
|
f (x)³ 0 |
( f (x)£ 0) для всех x Î (a,b); |
||
2) если производная |
′ |
′ |
|
f (x)> 0 |
( f (x)< 0) для всех x Î (a,b), то функция f |
||
строго возрастает (строго убывает) на [a, b].
Доказательство.
1) |
Необходимость. Пусть f (x) возрастает на [a, b]. Покажем, что |
f ′(x)³ 0 |
"x Î(a, b). Предположим противное, т. е. f ′(x0 )< 0 , x0 (a, b). Тогда по |
теореме Ферма (ДУ возрастания (убывания) функции в точке) функция f строго
убывает в точке x0 Î(a, b), что противоречит тому, что f (x) возрастает "x Î[a, b].
Достаточность. Пусть f |
′ |
|
||||
|
(x)³ 0 для всех x Î(a,b). Для любой пары точек |
|||||
x1 < x2 таких, |
что [x1, x2 ] (a, b), |
функция f на отрезке [x1, x2 ] удовлетворяет ус- |
||||
ловиям теоремы Лагранжа: |
|
|
|
′ |
||
c (x1, x2 ), для которой f (x2 )− f (x1 )= f (c)(x2 − x1 ). |
||||||
Так как c Î(x1, x2 )Ì (a, b), |
то f |
′ |
f (x2 )³ f (x1 ). Т. о., мы |
|||
(c)³ 0 и, следовательно, |
||||||
доказали, что функция |
f (x) возрастает на [a, b]. |
|
||||
|
′ |
для всех x Î(a,b). По схеме доказательства предыдущего |
||||
2) Пусть f (x)> 0 |
||||||
пункта с помощью формулы конечных приращений Лагранжа получаем |
||||||
|
|
|
|
|
′ |
|
|
|
|
f (x2 )- f (x1 )= f (c)(x2 - x1 ). |
|
||
Так как |
|
|
|
|
′ |
, то f (x2 )> f (x1 ), то |
c (x1, x2 ) (a, b), то f (c)> 0 и если x1 < x2 |
||||||
есть функция |
f (x) возрастает в строгом смысле на [a, b]. |
|
||||
51

Замечание. Условие f ′(x)> 0 ( f ′(x)< 0), будучи достаточным для строгого возрастания (убывания) функции, не является необходимым. Это видно на приме-
ре функции f (x) = x3 , которая строго возрастает, но f ′(0)= 0.
12.2 Локальный экстремум
Определение локального экстремума
Пусть функция f (x) определена в некоторой ε - окрестности точки x0 :
Oε (x0 ). Напомним:
Точка x0 Î X называется
1)точкой локального максимума (минимума);
2)точкой строгого локального максимума (строгого локального минимума),
если существует такая окрестность Oε (x0 )= (x0 − ε, x0 + ε ) этой точки, что, соот-
ветственно,
1) " x Î Oε (x0 ) f (x) £ f (x0 ) (f (x) ³ f (x0 ));
2) x Oε (x0 )\ {x0 } f (x) < f (x0 ) (f (x) > f (x0 )).
Точки локального максимума и минимума называют точками локального экстремума.
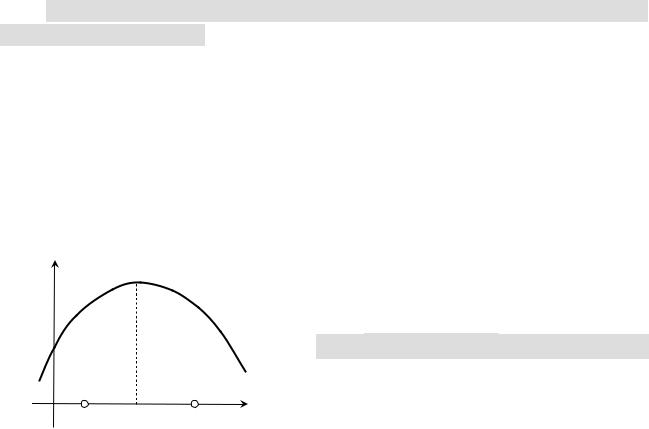
Теорема Ферма о необходимом условии локального экстремума
ТЕОРЕМА. Если функция y = f (x) имеет экстремум в точке x0 , то ее про-
изводная f ′(x0 ) = 0 либо равна нулю, либо не существует.
Доказательство в случае дифференцируемой функции в п. 10.1 Возрастание и убывание функции в точке.
Функция может иметь экстремум в точке и не быть дифференцируемой в этой точке. Примером служит функция f (x) = x , которая имеет минимум в точке x = 0, однако не имеет производной в этой точке.
52
Точки, в которых выполняется необходимое условие экстремума для непре-
рывной функции, называются критическими точками первого рода этой функции.
Ими являются корни уравнения f ′(x)= 0 (стационарные точки функции f ) или точки, в которых производная функции f не существует. Иногда критические
точки называют точками, «подозрительными на экстремум».
Замечание. Не в каждой своей критической точке функция обязательно
имеет экстремум. |
|
|
|
Пример 12.1. Рассмотрим функцию f (x) = x3 . |
Критической для функции |
||
′ |
|
2 |
= 0. Однако эта функ- |
является точка x = 0 , что следует из уравнения f (x) ≡ 3x |
|
||
ция строго возрастает и экстремумов не имеет.
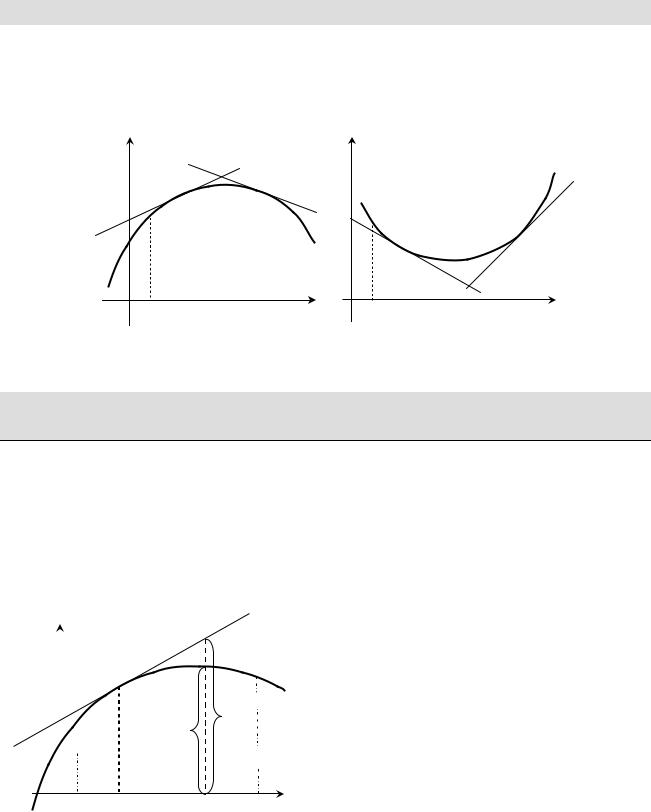
Достаточные условия экстремума Первое достаточное условие локального экстремума диффе-
ренцируемой функции
ТЕОРЕМА. Пусть функция f дифференцируема в некоторой окрестности
Oδ (x0 ) критической точки x0 , за исключением, быть может, самой точки x0 , и не-
прерывна в точке x0 . Если при переходе через точку x0 слева направо производ-
ная f ′ меняет знак с плюса на минус (с минуса на плюс), то в точке x0 функция f
имеет строгий локальный максимум (минимум).
Если же производная f ′ имеет
y
один и тот же знак слева и справа от точ-
ки x0 , то экстремума в этой точке нет.
x0 − δ |
x0 |
x0 + δ |
x |
Рис. 12.1
Доказательство.
Если производная f ′ меняет знак с
«+» на «–», то по теореме предыдущего пункта (необходимое и достаточное усло- вие возрастания (убывания) функций)
53

функция f (x) возрастает для значений x (x0 − δ, x0 ) и f (x) |
убывает для значе- |
o |
|
ний x (x0 , x0 + δ). Следовательно, x Oδ (x0 ) f (x0 ) > f (x) |
, то есть x0 – точка |
локального максимума функции f (x) (рис. 12.1). |
|
Аналогично доказывается теорема и в случае минимума. |
|
Второе достаточное условие локального экстремума дважды дифференцируемой функции
ТЕОРЕМА. Пусть функция f в критической точке x0 имеет конечную вто-
рую производную. Тогда функция имеет в точке x0 максимум, если |
f ′′(x0 ) < 0 , и |
|||||||||||||||||||
минимум, если f ′′(x0 ) > 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Запишем формулу Тейлора для функции |
f (x) в окрестности точки x0 |
при |
|
|||||||||||||||
n = 2: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
f (x)= f (x )+ |
f ′(x0 ) |
(x − x )+ |
f ′′(x0 ) |
(x − x )2 |
+o((x − x )2 ). |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
0 |
|
1! |
|
|
0 |
2! |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
По условию |
f ′(x0 )= 0, поэтому |
sgn(f (x)− f (x0 ))= sgn f ′′(x0 ) |
при |
|
x → x0 . |
||||||||||||||
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если |
|
f ′′(x0 ) > 0 x Oδ (x0 ) , то f (x) > |
f (x0 ) и, следовательно, x0 |
– точка локаль- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
o |
(x0 ) , то |
|
|
|
|
|
|
|
ного минимума функции f (x). Если же |
f ′′(x0 )< 0 x Oδ |
f (x) < f (x0 ) и, |
||||||||||||||||||
следовательно, x0 – точка локального максимума функции |
f (x). |
|
|
|
|
|
|
|
||||||||||||
|
Пример 12.2. Доказать неравенство 1+ 2ln x ≤ x2 |
для x > 0. |
|
|
|
|
|
|
||||||||||||
|
Рассмотрим функцию |
f (x) = x |
2 |
− 2ln x −1. Имеем |
f (1) = 0, |
f |
′ |
|
2(x2 −1) |
. |
||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
(x) = |
|
x |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для |
|
′ |
а для 0 |
< x < 1 f |
′ |
|
|
|
|
|
|
|
на интервале |
|||||||
x > 1 f (x) > 0, |
(x)< 0 . Таким образом, f (x) |
|||||||||||||||||||
(0, 1) |
|
убывает, на интервале |
(1, + ∞) |
возрастает, и так как |
f (x) |
непрерывна при |
||||||||||||||
54

x = 1, то |
точка |
x = 1 является |
точкой минимума. |
Следовательно, для |
x > 0 |
|||
f (x)= x2 |
- 2ln x -1³ f (1)= 0, откуда и вытекает неравенство x2 ³1+ 2ln x, x > 0. |
|||||||
|
|
|
|
|
|
(x -1)3 |
|
|
Пример 12.3. Исследовать на экстремум функцию y = 3(x + 1)2 . |
|
|||||||
Определим промежутки монотонности и экстремумы данной функции. Пер- |
||||||||
вая производная функции равна: |
y¢(x)= (x -1)2(x + 5). Находим критические точ- |
|||||||
|
|
|
|
|
3(x +1)3 |
|
|
|
ки: y′ = 0 при x =1, |
x = −5 и y′ не существует при x = −1. |
|
|
|||||
При x (− ∞; − 5), x (− 1;1)U (1; + ∞) |
y′ > 0 , при xÎ(- 5;1) |
y′ < 0 . На каж- |
||||||
дом из промежутков (− ∞; − 5], (−1;1], [1; + ∞) функция возрастает, на промежутке |
||||||||
[− 5;−1) убывает (рис. 12.2), в точке (−5; −4,5) имеет локальный максимум. Отме- |
||||||||
тим, что y′(1)= 0, т. е. график функции имеет в этой точке горизонтальную |
|
|||||||
|
y′ |
|
+ |
− |
+ |
+ |
|
|
|
у |
|
−5 |
−1 |
1 |
х |
|
|
|
|
|
|
Рис. 12.2 |
|
|
|
|
касательную, точка |
x =1 является критической, но |
локального |
экстремума у |
|||||
функции в этой точке нет, т. к. первая производная не меняет знак. Точка |
x = −1 |
|||||||
также не является точкой экстремума (заданная функция в ней не определена), хо- |
||||||||
тя производная при переходе через эту точку меняет знак. |
|
|
||||||
Полное исследование и построение графика функции приведены ниже (при- |
||||||||
мер 12.12). |
|
|
|
|
|
|
|
|
Пример 12.4. Исследовать на экстремум функцию y = e− x 2 .
Первая производная функции равна: y′ = −2xe− x 2 . Приравнивая производ-
ную нулю, находим единственную критическую точку x = 0. Далее находим вто-
55
рую производную y′′ = −2e− x2 + 4x2e− x 2 . Ее значение в точке x = 0равно − 2. Со-
гласно второму достаточному условию локального экстремума делаем вывод о наличии максимума функции и вычисляем ymax (0) = e0 = 1.
Абсолютный экстремум функции
Для функции f (x) – непрерывной на отрезке [a, b] – понятие absextr f (x)
x [a, b]
объединяет понятия наибольшего и наименьшего значений функции на отрезке,
т.е. наиб f (x) и наим f (x).
x [a, b] x [a, b]
Наибольшее (наименьшее) значение непрерывной на отрезке [a;b] функции
f (x) достигается либо в критической точке этой функции, либо в граничных точ-
ках а и b этого отрезка.
Для нахождения наиб f (x) и наим f (x) непрерывной на [a, b] функции ис- |
|||
|
|
x [a, b] |
x [a, b] |
пользуется следующая схема решения: |
|||
1. |
Найти критические точки функции f (x), т.е. те значения x [a, b], при |
||
которых либо f |
′ |
′ |
|
(x) = 0, либо f |
(x) не существует (но в этих точках сама функция |
||
f (x) определена и непрерывна). |
|||
2. |
Вычислить значения функции в найденных точках и на концах отрезка |
||
[a, b]. |
|
|
|
3. |
Найти |
наиб f (x) и |
наим f (x). Для этого нужно сравнить значения |
|
|
x [a, b] |
x [a, b] |
функции в критических точках (внутри отрезка) со значениями функции в гранич- ных точках отрезка и выбрать среди них наибольшее и, соответственно, наимень- шее значение. (При этом не требуется анализ характера экстремума этих точек).
|
Иногда |
вместо наиб f (x) и |
наим f (x) записывают соответственно |
|
|
|
|
x [a, b] |
x [a, b] |
max |
f (x) и |
min |
f (x). |
|
x [a, b] |
|
x [a, b] |
|
|
|
|
|
|
56 |
12.3 Выпуклость и точки перегиба графика функции
Определение.
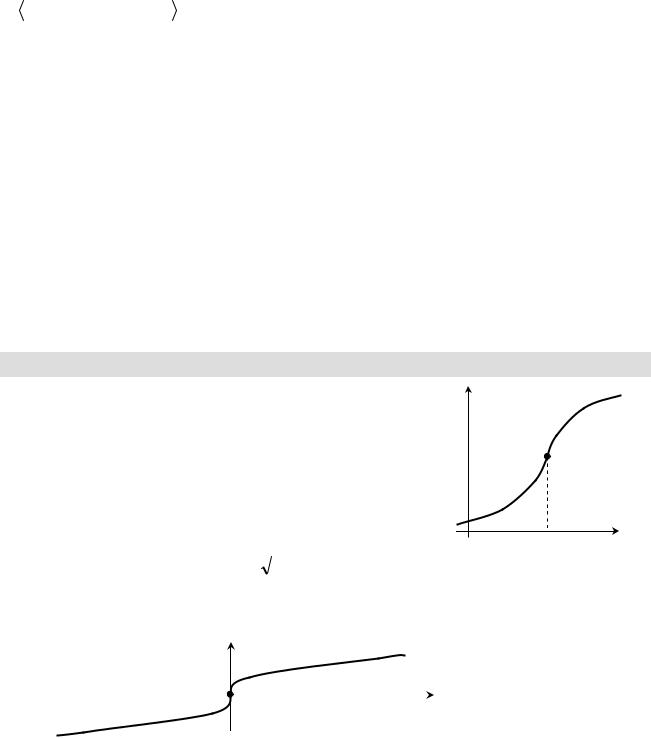
График дифференцируемой функции f называется выпуклым вверх (выпук-
лым вниз) в интервале ( a,b), если он расположен не выше (не ниже), любой своей
y |
y |
a |
b |
x |
a |
b |
x |
|
|
||||
|
|
Рис. 12.3 |
|
|
|
касательной к графику функции на этом интервале.
Теорема о достаточном условии выпуклости вниз (вверх) графика функции на данном интервале
ТЕОРЕМА. |
Если функция f |
имеет на интервале (a,b) вторую производ- |
||||
′′ |
|
′′ |
|
|
|
|
ную и f (x) ³ 0 ( f |
(x)≤ 0) для x (a,b), то график функции имеет на (a,b) вы- |
|||||
пуклость, направленную вниз (вверх). |
|
|||||
|
|
|
|
|||
Доказательство. |
|
|
|
|||
|
|
′′ |
x (a, b) и докажем, что ее график является вы- |
|||
Допустим, что f (x)≤ 0 |
||||||
y |
|
|
|
|
пуклым вверх. Через точку M 0 прове- |
|
|
M 0 |
|
|
|
дем касательную к графику функции |
|
|
|
|
|
y = f (x) . Для доказательства теоремы |
||
|
|
Y |
|
|
мы должны установить, что график |
|
|
|
|
|
функции на (a,b) расположен не выше |
||
|
y = f (x) |
|
|
|||
|
|
|
|
|
своей касательной на этом интервале. |
|
|
|
|
|
x |
Пусть x – произвольная точка из (a,b), |
|
a |
x0 |
x |
b |
y = f (x) – ордината графика функции в |
||
|
||||||
Рис. 12.4 |
точке |
x . Далее |
57 |
|
|
|
|
Y = f (x0 ) + f ′(x0 )(x − x0 ) – ордината касательной, соответствующая значению x .
Найдем y −Y = f (x) − f (x0 ) − f ′(x0 )(x − x0 )=
= теорема Лагранжа = f ¢(с)(x - x0 )- f ¢(x0 )(x - x0 )= |
|
êéx0 < c < x, |
|
= |
|
|
|||
|
|
ë x < c < x0 |
|
|
= (x − x0 )(c − x0 )f ′′(с1) , с1 (x0 , c)либо с1 (c, x0 ). Имеем |
|
|
||
(x - x0 )(c - x0 )> 0 , |
(12.3.1) |
|||
так как либо (x − x0 > 0) (c − x0 )> 0, либо (x0 − x > 0) (x0 − c)> 0. По условию теоремы f ′′(c1 )£ 0. Поэтому, с учетом (12.3.1), y −Y ≤ 0, y ≤ Y , т. е. график функ-
ции y = f (x) направлен выпуклостью вверх на (a,b).
Аналогично доказывается, что при f ′′(x) ³ 0 график функции является вы-
пуклым вниз. Теорема доказана.
Точки перегиба графика функции
Определение.
Точка M 0 (x0 , f (x0 ) |
называется точкой пере- |
y |
||
гиба графика функции y = f (x) , если существует |
|
|||
такая окрестность точки |
x0 , в пределах которой, |
|
||
слева и справа от нее, направления выпуклости |
|
|||
графика функции различны. |
|
|||
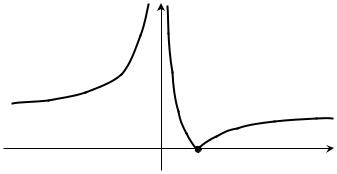
Пример 12.5. Для |
f (x) = 3 |
|
график функ- |
|
x |
|
|||
ции (рис. 12.6) выпуклый вниз на (− ∞, 0) и выпуклый вверх на
M 0
x0 x
Рис. 12.5
(0, + ∞). Точка пе-
y |
региба графика функ- |
|
ции (0; 0). |
||
|
||
0 |
x |
Рис. 12.6
58
|
|
x −1 |
|
|
|
|
|||||||
|
Пример 12.6. Для f (x) = |
|
|
график функции (см. рисунок 12.7) |
выпук- |
||||||||
|
|
||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лый вниз на (− ∞, 0) и на (0, 1), |
|||
|
|
|
|
|
|
|
|
|
|
выпуклый |
вверх |
на |
(1, + ∞). |
|
|
|
|
|
|
|
|
|
|
Точка перегиба графика функ- |
|||
|
|
1 |
|
|
|
|
|
|
|
ции (1; 0). |
Заметим, что здесь |
||
|
|
|
|
|
|
|
|
x |
точка x =1 является точкой ло- |
||||
|
|
0 |
1 |
|
|
|
|
кального минимума функции. |
|||||
|
|
|
|
|
|
|
|
||||||
|
|
Рис. 12.7 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
||||||||||
|
ТЕОРЕМА о необходимом условии существования точки перегиба |
|
|||||||||||
|
|
|
|||||||||||
|
Если функция y = f (x) имеет перегиб в точке M 0 (x0 , f (x0 ) , то f ′′(x0 ) =0, |
||||||||||||
или f ′′(x0 ) не существует. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
|
Доказательство. |
|
|
|
|
|
|
|
|
||||
|
Пусть точка M 0 (x0 , f (x0 ) разделяет промежутки выпуклости вниз и вверх |
||||||||||||
(Рис. 12.5). Пусть при |
x < x0 кривая |
y = f (x) выпукла вниз, а при |
x > x0 |
кривая |
|||||||||
y = f (x) |
выпукла вверх. Тогда при x < x0 вторая производная |
′′ |
³ 0 и, |
значит, |
|||||||||
f (x) |
|||||||||||||
′ |
|
|
′′ |
£ |
|
0 и, значит, |
′ |
|
|
|
|||
f (x) возрастает. При |
x > x0 f (x) |
|
f (x) убывает. Это означает, что |
||||||||||
функция |
′ |
максимум |
в |
точке x0 , |
следовательно, ее |
производная |
|||||||
f (x) имеет |
|||||||||||||
′ |
′ |
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
( f (x)) = f (x) в этой точке или равна нулю, или не существует. |
|
|
|||||||||||
|
Замечание. Необходимое условие точки перегиба не является достаточным. |
||||||||||||
Например, кривая y = x4 является выпуклой вниз, так как y¢¢ º12x2 ³ 0 и, |
значит, |
||||||||||||
не имеет точек перегиба, хотя y′′ = 0 при x = 0. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Точки, в которых f ′′(x0 ) =0 или f ′′(x0 ) |
не существует, называют крити- |
|||||||||||
ческими точками второго рода.
59

Чтобы выяснить, является ли критическая точка точкой перегиба, нужны достаточные условия.
ТЕОРЕМА о достаточных условиях существования точки перегиба
Пусть функция f (x) определена в окрестности точки x0 , в которой либо f ′′(x0 ) =0, либо f ′′(x0 ) не существует и пусть f (x) дважды непрерывно диффе-
ренцируема хотя бы в проколотой окрестности этой точки. Точка M (x0 , f (x0 ) яв-
ляется точкой перегиба графика функции, если f ¢¢(x) меняет знак при переходе
через точку x0 .
Доказательство.
Пусть, например, вторая производная |
f |
′′ |
′′ |
(x) ³ 0 при x < x0 и |
f (x) £ 0 |
||
при x > x0 . В этом случае (Рис. 12.5) слева от x0 |
график функции выпуклый вниз, |
||
а справа от x0 выпуклый вверх, т. е. M (x0 , f (x0 ) |
– точка перегиба графика функ- |
||
ции. |
|
|
|
Пример 12.7. Исследовать на выпуклость, найти точки перегиба графика функции y = ln(x2 − 2x + 2).
Область определения x R . При x =1 значение функции y = 0. Производная |
|
|||||||||
y′ = |
2x − 2 |
. Точка |
x =1 является точкой минимума функции; y |
min |
= y(1)= 0. |
|||||
x2 − 2x + 2 |
||||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
′′ |
|
− 2x(x − 2) |
|
|
|
|
|
|
|
|
= (x2 − 2x + 2)2 . Знаки второй производной: |
′′ |
|
|||||
Вторая производная y |
|
y |
(x)< 0 |
при |
||||||
x (− ∞; 0), x (2; + ∞), |
y′′ (x)> 0 при x (0; 2). При x (− ∞; 0) и x (2; + ∞) гра- |
|||||||||
фик функции выпуклый вверх; на (0; 2) – выпуклый вниз. График меняет направ-
ление выпуклости в двух точках: x = 0 и x = 2 (рис. 12.8). Поэтому точки перегиба графика функции (0; ln 2) и (2; ln 2).
60
