Дифф_Исчисление_11

ЛЕКЦИЯ 9. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ

Ø Дифференциал функции одной переменной

üПонятие первого дифференциала. Геометрический смысл

üДифференциал и приближенные вычисления

üПравила вычисления дифференциала суммы, разности, произведения

üВычисление дифференциала сложной функции. Инвариантность формы

первого дифференциала

Ø Производные и дифференциалы высших порядков

üПонятие производной n -го порядка

üДифференциалы высших порядков. Сохраняется ли свойство инвариантно- сти для дифференциалов высших порядков?

üПравила вычисления производной суммы n -го порядка. Формула Лейбница для n -й производной произведения двух функций

9.1 Дифференциал функции одной переменной

Понятие первого дифференциала. Геометрический смысл

т. е. разность y − dy имеет более высокий порядок малости по сравнению с Dx .

По этой причине говорят, что дифференциал есть главная часть приращения

то есть отношение дифференциалов df (x0 ) и dx равно f ′(x0 ). По этой причине,

следуя Лейбницу, производную часто обозначают символом dfdx(x) наряду с пред-

ложенным впоследствии Лагранжем символом f ′(x0 ).

(Ж.Л. Лагранж (1736-1813) – знаменитый французский математик и механик.)

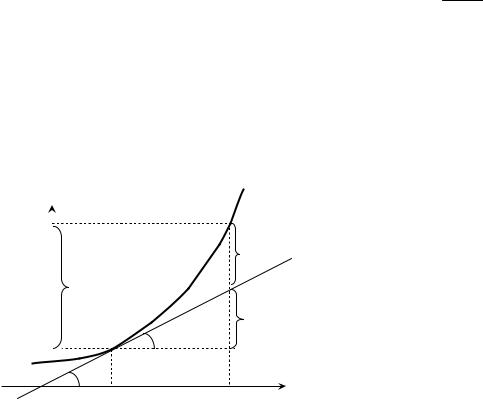
Геометрический смысл дифференциала

Посмотрим на дифференциал с геометрической точки зрения (рис. 9.1).

y

Рис. 9.1

22

На рисунке к графику функции f (x) проведена касательная в точке А с абсциссой

x0 . Согласно (9.1.1) dy = d f (x0 )= f ′(x0 )Dx = tg a× Dx = CD – приращение ордина-

ты касательной к графику функции y = f (x)в точке x0 . При этом разность

BC = Df (xo )- df (x0 )= o(Dx) – бесконечно малая более высокого порядка, чем x .

Этим часто пользуются для приближенного вычисления значений дифференци-

руемой функции из некоторой ε - окрестности точки x0 X при достаточно ма-

лом ε > 0. Для этого формулу (9.1.2) записывают в виде

(x0 , f (x0 )) – доставляет линейное приближение функции f в окрестности точки x0 .

Следовательно, геометрически (9.1.4) означает, что в окрестности точки (x0 , f (x0 ))

график функции y = f (x) сливается с отрезком касательной, т. е. «спрямляется».

Говорят, что соотношением (4) функция y = f (x) линеаризована в окрестности точки x0 .

23

Если аргумент х вычислен с относительной погрешностью dx = xx , то зна-

Пример 9.1. Найти время удвоения вклада в банк, если ставка банковского процента за год составляет 10 % годовых.

Найдем количество лет Т, в течение которых сумма вклада увеличится в 2

2.На сколько процентов увеличится площадь круга, если его радиус увеличится на 1%?

3.Известно, что x ≈ 0,5 и x3 - x » 0 . С какой точностью выполняется приближен-

ное равенство x ≈ 0,5, если x3 - x » 0 выполняется с точностью 0,001.

4. На сколько процентов изменится величина степени 2,13,2 при изменении осно-

вания степени на 3%?

9.2 Производные и дифференциалы высших порядков

Понятие производной n -го порядка

Пусть для функции f : X → R множество X не имеет изолированных точек

зывается первой производной функции f и обозначается f ′ . Индукцией опреде-

лим производную функции f произвольного порядка. Если функция f (n−1) (n Î N)

f (n) := (f (n−1) )′, f (0) := f .

25

При этом функция f называется n − дифференцируемой ( n раз дифференцируе-

мой) на X .

Дифференциалы высших порядков

Дифференциалы высших порядков (как и старшие производные) определя- ются индуктивно.

Пусть функция y = f (x) дифференцируема в каждой точке x X . Если в точке x дифференциал

d ( f (x)) = f ′(x)dx = f ′(x) x

является дифференцируемой функцией, то существует дифференциал от диффе-

ренциала d(dy)= d(df )(x0 ) данной функции, который называется вторым диффе-

ванное приращение независимой переменной x , т. е. является постоянной величи- ной и d(dx)= d( x)= 0. Поэтому

представлена как обыкновенная дробь – отношение дифференциалов n − го поряд-

ка функции f и n − й степени дифференциала аргумента.

2. Рассмотрим случай зависимой переменной. Пусть y = f (x), где x = x(t) –

дифференцируемая функция. В силу инвариантности формы первого дифферен-

переменная, делаем вывод, что уже второй дифференциал инвариантностью фор- мы не обладает.

Упражнение. Пусть x = x(t) = kt + b, k, b R . Показать, что для случая ли-

нейной внутренней функции свойство инвариантности дифференциалов высших порядков сохраняется.

Приведем без доказательства теорему.

Правила вычисления производной суммы n -го порядка. Формула Лейбница для n -й производной произведения двух функций

ТЕОРЕМА. Если функции u(x), v(x) имеют в точке x0 производные поряд-

ка n , то в этой точке существуют производные порядка n суммы и произведения этих функций и выполняются равенства:

Эти формулы нетрудно проверить методом математической индукции. Равенство (9.2.4) называют формулой Лейбница для n-й производной про-

изведения двух функций.

Пример 9.5. Для функции y(x)= (x3 + 5x - 6)e4x в точке x = 0 найти произ-

водную 10-го порядка.

Решение. Заданная функция представляет собой произведение двух функций. В этом случае для нахождения n-й производной нужно применить формулу

Лейбница

Так как (x3 - 5x + 6)(4) = K = (x3 - 5x + 6)(10) = 0, все остальные слагаемые равны нулю. Находим производные:

(e4x )(10) = e4 x × 410 , (e4x )(9) = e4x × 49 , (e4 x )(8) = e4x × 48 , (e4x )(7) = e4x × 47 ,

(x3 - 5x + 6)(1) = 3x2 - 5, (x3 - 5x + 6)(2) = 6x, (x3 - 5x + 6)(3) = 6.

28

9.5 Производная функции, заданной параметрически. Дифференцирование функций, заданных неявно

29

ЛЕКЦИЯ 10. ТЕОРЕМЫ О НЕПРЕРЫВНЫХ И ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ

Ø Возрастание и убывание функции в точке

Ø Формулы конечных приращений, их приложения ü Теорема Ролля о среднем. Геометрический смысл

ü Теорема Лагранжа о среднем, ее геометрический и экономический смысл

Следствия из теоремы Лагранжа

ü Теорема Коши (обобщение формулы конечных приращений)

Ø Раскрытие неопределенностей (Правило Лопиталя)

10.1 Возрастание и убывание функции в точке

Пусть функция f : X → R определена на множестве X и x0 X – пре-

дельная точка множества X .

Определение.

Функция f называется строго возрастающей (строго убывающей) в точке

x 0 , если существует такая окрестность Oε (x0 )= (x0 − ε, x0 + ε ) этой точки, что

Если в этих неравенствах знаки > и <

у

30